Mẹ mua cho Mai một hộp sữa tươi loại 1 000 ml. Ngày đầu Mai uống 1/5 hộp; ngày tiếp theo Mai uống tiếp 1/4 hộp.a) Hỏi sau hai ngày hộp sữa tươi còn lại bao nhiêu phần?b) Tính lượng sữa tươi còn lại sau hai ngày.

Câu hỏi:

Trả lời:

a) Sau hai ngày Mai đã uống số phần của một hộp sữa tươi là: $\frac{1}{5} + \frac{1}{4} = \frac{4}{20} + \frac{5}{20} = \frac{9}{20}$ (phần)Sau hai ngày hộp sữa tươi còn lại: $1 - \frac{9}{20} = \frac{11}{20}$ (phần)b) Lượng sữa tươi còn lại số ml là: $1 000 . \frac{11}{20} = 50.11 = 550$ (ml) Vậy sau hai ngày hộp sữa còn lại $\frac{11}{20}$ phần và còn lại 550 ml.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Lý thuyết Toán lớp 6 Chương 6 (Kết nối tri thức 2023): Phân số hay, chi tiết

Lý thuyết Toán lớp 6 Chương 6: Phân số

Video giải Toán 6 Bài tập cuối chương 6 trang 27 – Kết nối tri thức

I. Lý thuyết Toán lớp 6 Chương 6: Phân số

1. Phân số

– Định nghĩa về phân số: Với a, b ∈ ℤ ,b ≠ 0 , ta gọi 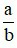 là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.

Chú ý: Mọi số nguyên đều có thể viết dưới dạng phân số.

2. Hai phân số bằng nhau

Hai phân số  và  được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là  .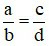

3. Tính chất cơ bản của phân số

– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

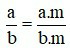với a, b, m ∈ ℤ; b≠0;m≠0.

– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.

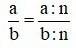với n là ước chung của a và b; a, b ∈ ℤ; b≠0.

4. Quy đồng mẫu nhiều phân số

Để quy đồng hai hay nhiều phân số ta làm như sau:

Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.

Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

5. So sánh hai phân số

a) So sánh hai phân số cùng mẫu

– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.

b) So sánh hai phân số không cùng mẫu

– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

6. Hỗn số dương

– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi 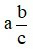 là một hỗn số dương với a là phần nguyên và  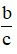 là phần phân số.

– Muốn đổi từ hỗn số sang phân số ta làm như sau:

Bước 1: Giữ nguyên phần mẫu số.

Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.

– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:

Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.

Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.

7. Phép công hai phân số

a) Cộng hai phân số cùng mẫu

– Muốn cộng hai phân số cùng mẫu, ta cộng các tử và giữ nguyên mẫu:

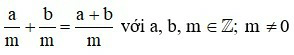
b) Cộng hai phân số không cùng mẫu số

– Muốn cộng hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử và giữ nguyên mẫu.

c) Số đối

– Hai số được gọi là đối nhau nếu tổng của chúng bằng 0. Kí hiệu số đối của phân số 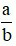 là  .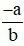

8. Tính chất của phép cộng hai phân số

Cho hai phân số 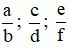  với a, b, c, d, e, f ∈ ℤ; b ≠ 0; d ≠ 0, f ≠ 0. Ta có:

+ Tính chất giao hoán:

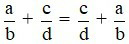
+ Tính chất kết hợp:

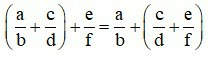
+ Tính chất cộng với số 0:

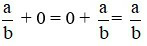
9. Phép trừ hai phân số

a) Trừ hai phân số cùng mẫu

– Muốn trừ hai phân số cùng mẫu, ta lấy tử số của phân số thứ nhất trừ đi tử số của phân số thứ hai và giữ nguyên mẫu số.

với a, b, m ∈ ℤ; m ≠ 0.

b) Trừ hai phân số không cùng mẫu:

– Muốn trừ hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số rồi trừ hai phân số đó.

10. Phép nhân hai phân số

– Muốn nhân hai phân số, ta nhân các tử số với nhau và các mẫu số với nhau.

Cho a, b, c, d ∈ ℤ; b ≠ 0; d≠0.

Khi đó phép nhân hai phân số ta có:

11. Tính chất của phép nhân

Cho 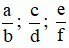  là các phân số với a, b, c, d, e, f ∈ ℤ; b ≠ 0; d ≠ 0, f ≠ 0.

Khi đó ta có các tính chất của phép nhân như sau:

+ Tính giao hoán:

+ Tính kết hợp:

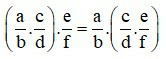
+ Tính nhân với 1:

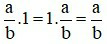
+ Tính phân phối giữa phép nhân với phép cộng:

12. Phép chia phân số

a) Phân số nghịch đảo:

Phân số này được gọi là nghịch đảo của phân số kia nếu tích của chúng bằng 1

Cho a, b ∈ ℤ; a, b ≠ 0

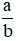Phân số  là phân số nghịch đảo của phân số  vì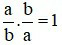

b) Phép chia phân số

– Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.

với a, b, c, d ∈ ℤ; b ≠ 0; c ≠ 0; d ≠ 0

13. Tìm giá trị phân số của một số cho trước

Muốn tìm 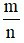 của một số a cho trước ta tính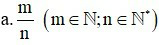

14. Tìm một số khi biết giá trị phân số của nó

– Muốn tìm một số biết  của số đó bằng b, ta tính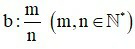

II. Bài tập vận dụng

Bài 1: Sắp xếp các phân số sau theo thứ tự tăng dần

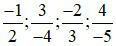
Lời giải:

Ta có:

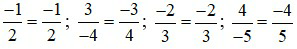
BCNN (2; 3; 4; 5) = 60

Ta có: –48 < –45 < –40 < –30 do đó:

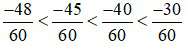
Hay

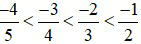
Hay sắp xếp theo thứ tự tăng dần là:

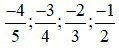
Bài 2: Thực hiện phép tính

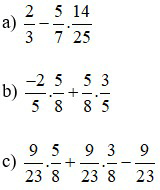
Lời giải:

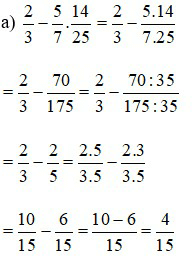
Bài 3: Tìm x

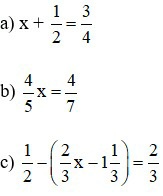
Lời giải:

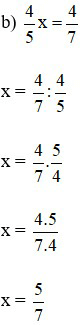
Bài 4: Một tấm vải dài 20 m, người thứ nhất mua 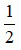 tấm vải, người thứ hai mua   tấm vải còn lại. Hỏi sau hai lần bán còn lại bao nhiêu m vải.

Lời giải:

Người thứ nhất đã mua số m vải là

Số m vải còn lại sau khi bán cho người thứ nhất là

20 – 10 = 10 (m)

Số m vải bán cho người thứ hai là

10. = 5 (m)

Số m vải còn lại sau khi bán cho cả hai người là

20 – 10 – 5 = 5 (m)

Bài 5: Một kho hàng có một số hàng. Biết  kho hàng có 1250 sản phẩm. Hỏi   kho hàng có bao nhiêu sản phẩm.

Lời giải:

Số sản phẩm trong kho hàng là:

kho hàng có số sản phẩm là:

Vậy   kho hàng có 500 sản phẩm.

Xem thêm các bài tóm tắt lý thuyết Toán 6 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Chương 5: Tính đối xứng của hình phẳng trong tự nhiên

Lý thuyết Chương 6: Phân số

Lý thuyết Chương 7: Số thập phân

Lý thuyết Chương 8: Những hình học cơ bản

Lý thuyết Chương 9: Dữ liệu và xác suất thực nghiệm
Sách bài tập Toán 6 (Kết nối tri thức) Ôn tập chương 6

Giải SBT Toán lớp 6 Ôn tập chương 6

Bài tập trắc nghiệm

(Có thể chọn nhiều đáp án)

Bài 1 trang 21 sách bài tập Toán lớp 6 Tập 2: Khẳng định nào sau đây là sai?

A. Muốn cộng hai phân số có cùng mẫu, ta cộng tử với tử và giữ nguyên mẫu

B. Muốn cộng hai phân số, ta cộng tử với tử và mẫu với mẫu

C. Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau

D. Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia

Lời giải:

Các khẳng định A, C, D đúng.

Phát biểu B sai vì muốn cộng hai phân số, ta đưa chúng về dạng 2 phân số có cùng mẫu số rồi cộng tử với tử và giữ nguyên mẫu.

Vậy khẳng định sai là: B. Muốn cộng hai phân số, ta cộng tử với tử và mẫu với mẫu.

Bài 2 trang 21 sách bài tập Toán lớp 6 Tập 2: Khẳng định nào sau đây là sai?

A. 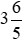 là một hỗn số dương

B.

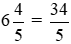
C. Phân số  bằng phân số

D. Phân số  biểu thị thương của phép chia 10 cho 4

Lời giải:

Ta lần lượt kiểm tra các khẳng định trên.

– Khẳng định A.  là một hỗn số dương

Ta thấy  có phần phân số

Mà phần phân số của hỗn số luôn nhỏ hơn 1.

Suy ra  không phải là một hỗn số.

Do đó khẳng định A sai.

– Khẳng định B. >

Ta có:

Do đó khẳng định B đúng.

– Khẳng định C. Phân số 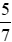 bằng phân số

Cách 1: Nhân cả tử và mẫu số của phân số với (−1), ta được:

Do đó khẳng định C đúng.

Cách 2: Nhân cả tử và mẫu số của phân số  với (−1), ta được:

Do đó khẳng định C đúng.

– Khẳng định D. Phân số  biểu thị thương của phép chia 10 cho 4 là khẳng định đúng.

Vậy khẳng định sai là: A.  là một hỗn số dương.

Bài 3 trang 21 sách bài tập Toán lớp 6 Tập 2: Khẳng định nào sau đây là sai?

A. 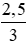 là một phân số

B. Mọi số nguyên đều viết được dưới dạng phân số

C. Mỗi phân số khác 0 luôn có phân số nghịch đảo

D. Phân số 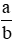  bằng phân số  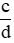nếu a . d = b . c

Lời giải:

Ta lần lượt kiểm tra các khẳng định trên.

– Khẳng định A.  là một phân số

Phân số có dạng (a, b là các số nguyên, b khác 0).

Mà 2,5 không là số nguyên

Nên  không phải là một phân số.

Do đó khẳng định A sai.

– Khẳng định B. Mọi số nguyên đều viết được dưới dạng phân số

Mọi số nguyên đều viết được dưới dạng phân số có mẫu số là 1.

Do đó khẳng định B đúng.

– Khẳng định C. Mỗi phân số khác 0 luôn có phân số nghịch đảo là khẳng định đúng.

– Khẳng định D. Phân số  bằng phân số  nếu a . d = b . c là khẳng định đúng.

Vậy khẳng định sai là: A.  là một phân số.

Bài 4 trang 21 sách bài tập Toán lớp 6 Tập 2: Các khẳng định nào sau đây là đúng?

A. Phân số tối giản là phân số mà tử số và mẫu số chỉ có ước chung là 1 và −1

B. Phân số tối giản là phân số mà tử số và mẫu số chỉ có ước chung là 1

C. Phân số tối giản là phân số mà tử số và mẫu số chỉ có ước chung là −1

D. Mọi phân số đều rút gọn được về phân số tối giản

Lời giải:

Ta lần lượt kiểm tra các khẳng định trên.

– Khẳng định A đúng.

– Khẳng định B sai vì còn thiếu một ước chung là −1.

– Khẳng định C sai vì còn thiếu một ước chung là 1.

– Khẳng định D đúng.

Vậy các khẳng định đúng là khẳng định A và D.

Bài 5 trang 21 sách bài tập Toán lớp 6 Tập 2: Các khẳng định nào sau đây là đúng?

A. Phân số 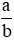 bằng phân số  với m là số nguyên khác 0

B. Phân số  bằng phân số  với m là một ước chung của a, b

C. Phân số  bằng phân số

D. Mọi phân số có mẫu âm đều viết được dưới dạng phân số bằng nó có mẫu dương

Lời giải:

Ta lần lượt kiểm tra các khẳng định trên.

– Khẳng định A là đúng (theo tính chất 1).

– Khẳng định B là đúng (theo tính chất 2).

– Khẳng định C.

Nhân cả tử và mẫu của phân số  với (−5), ta được:

Do đó khẳng định C sai.

– Khẳng định D đúng vì khi nhân cả tử và mẫu của phân số có mẫu âm với cùng một số nguyên âm thì ta được một phân số mới có mẫu dương.

Vậy các khẳng định đúng là khẳng định A, B và D.

Bài tập

Bài 6.48 trang 22 sách bài tập Toán lớp 6 Tập 2: Viết số đo thời gian sau đây theo đơn vị giờ, dưới dạng phân số tối giản:

36 phút; 18 phút; 150 phút.

Lời giải:

Đổi: 1 giờ = 60 phút.

Do đó khi đổi từ phút sang giờ, ta lấy số phút chia cho 60.

Viết phân số với tử số là số đo thời gian (phút), mẫu là 60 rồi rút gọn về dạng phân số tối giản.

Các đơn vị đo thời gian được đổi sang giờ (viết dưới dạng phân số tối giản) như sau:

Vậy các số đo thời gian: 36 phút; 18 phút; 150 phút viết theo đơn vị giờ (dưới dạng phân số tối giản) lần lượt là:

Bài 6.49 trang 22 sách bài tập Toán lớp 6 Tập 2: Tính một cách hợp lí:

Lời giải:

Bài 6.50 trang 22 sách bài tập Toán lớp 6 Tập 2: quả dưa hấu nặng  kg. Hỏi quả dưa hấu nặng bao nhiêu kilôgam?

Lời giải:

Bài 6.51 trang 22 sách bài tập Toán lớp 6 Tập 2: Tính giá trị biểu thức:

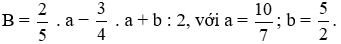
Lời giải:

Bài 6.52 trang 22 sách bài tập Toán lớp 6 Tập 2: Bạn Hà đọc một cuốn sách trong ba ngày. Ngày thứ nhất, Hà đọc được  số trang sách. Ngày thứ hai, Hà đọc  số trang còn lại. Ngày thứ ba đọc nốt 90 trang. Hỏi cuốn sách có bao nhiêu trang?

Lời giải:

Sau ngày thứ nhất, Hà còn lại:

Ngày thứ hai, Hà đọc được:

Số trang Hà đọc trong hai ngày đầu là:

Số trang Hà đọc trong ngày thứ ba bằng số phần của cuốn sách là:

Số trang của cuốn sách là:

Vậy cuốn sách 200 trang.

Bài 6.53 trang 22 sách bài tập Toán lớp 6 Tập 2: Tính giá trị biểu thức:

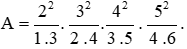
Lời giải:

Bài 6.54 trang 22 sách bài tập Toán lớp 6 Tập 2: Nhân dịp tết Trung thu, Hải xin phép mẹ mua món đồ chơi hết 50 000 đồng. Số tiền này bằng  số tiền Hải tiết kiệm được. Hỏi Hải đã tiết kiệm được bao nhiêu tiền?

Lời giải:

Hải đã tiết kiệm được số tiền là:

Vậy Hải đã tiết kiệm được 125 000 đồng.

Bài 6.55 trang 22 sách bài tập Toán lớp 6 Tập 2: Cả ba vòi cùng chảy vào một cái bể cạn. Nếu hai vòi I và II cùng chảy thì bể đầy sau 60 phút. Nếu hai vòi II và III cùng chảy thì bể đầy sau 75 phút. Nếu hai vòi III và I cùng chảy thì bể đầy sau 50 phút.

Lời giải:

a) Nếu cả ba vòi cùng chảy thì bể đầy sau bao lâu?

b) Nếu riêng mỗi vòi chảy một mình thì bể đầy sau bao lâu?

Lời giải:

Trong 1 phút:

a) Trong một phút, vòi I và II chảy được số phần của bể là:

Trong một phút, vòi II và III chảy được số phần của bể là:

Trong một phút, vòi I và III chảy được số phần của bể là:

Trong một phút, hai lần cả hai vòi chảy được số phần của bể là:

Trong một phút, cả hai vòi chảy được số phần của bể là:

Thời gian cả ba vòi cùng chảy từ khi bể chưa có nước đến khi đầy bể là:

Vậy nếu cả ba vòi cùng chảy thì đầy bể sau 40 phút.

b) Trong một phút, vòi I chảy được số phần của bể là:

Thời gian vòi I chảy một mình từ khi chưa có nước đến khi đầy bể là:

Trong một phút, vòi II chảy được số phần của bể là:

Thời gian vòi II chảy một mình từ khi chưa có nước đến khi đầy bể là:

Trong một phút, vòi III chảy được số phần của bể là:

Thời gian vòi III chảy một mình từ khi chưa có nước đến khi đầy bể là:

Vậy nếu riêng mỗi vòi chảy một mình thì vòi I sau đầy bể sau phút, vòi II đầy bể sau 200 phút, vòi III đầy bể sau 120 phút.
Thay số thích hợp vào dấu “?”.-1016=?56=-20?=50?

Câu hỏi:

Thay số thích hợp vào dấu “?”. $\frac{- 10}{16} = \frac{?}{56} = \frac{- 20}{?} = \frac{50}{?}$

Trả lời:

Ta có: $\frac{- 10}{16} = \frac{- 5}{8}$ Do đó: $\frac{- 5}{8} = \frac{?}{56} = \frac{- 20}{?} = \frac{50}{?}$ +) Với $\frac{- 5}{8} = \frac{?}{56}$ , vì 56 : 8 = 7 nên thừa số phụ là 7, do đó “?” = (-5).7 = -35+) Với $\frac{- 5}{8} = \frac{20}{?}$ , vì (-20) : (-5) = 4 nên thừa số phụ là 4, do đó “?” = 8.4 = 32+) Với $\frac{- 5}{8} = \frac{50}{?}$ , vì 50) : (-5) = -10 nên thừa số phụ là -10, do đó “?” = 8. (-10) = -80Vậy $\frac{- 5}{8} = \frac{- 35}{56} = \frac{- 20}{32} = \frac{50}{- 80}$

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Tính một cách hợp lí.a) A = -314+213+-2514+-1513;b) B = 53.725+53.2125-53.725

Câu hỏi:

Tính một cách hợp lí.a) A = $\frac{- 3}{14} + \frac{2}{13} + \frac{- 25}{14} + \frac{- 15}{13}$ ;b) B = $\frac{5}{3} . \frac{7}{25} + \frac{5}{3} . \frac{21}{25} - \frac{5}{3} . \frac{7}{25}$

Trả lời:

a) A = $\frac{- 3}{14} + \frac{2}{13} + \frac{- 25}{14} + \frac{- 15}{13}$ = $(\frac{- 3}{14} + \frac{- 25}{14}) + (\frac{2}{13} + \frac{- 15}{13})$ = $(\frac{- 28}{14}) + (\frac{- 13}{13})$ = (-2) + (-1) = -3b) B = $\frac{5}{3} . \frac{7}{25} + \frac{5}{3} . \frac{21}{25} - \frac{5}{3} . \frac{7}{25}$ = $\frac{5}{3} . (\frac{7}{25} + \frac{21}{25} - \frac{7}{25})$ = $\frac{5}{3} . \frac{21}{25}$ = $\frac{7}{5}$

====== **** mời các bạn xem câu tiếp bên dưới **** =====
Một bác nông dân thu hoạch và mang cà chua ra chợ bán. Bác đã bán được 20 kg, ứng với 2/5 số cà chua. Hỏi bác nông dân đã mang bao nhiêu kilôgam cà chua ra chợ bán?

Câu hỏi:

Một bác nông dân thu hoạch và mang cà chua ra chợ bán. Bác đã bán được 20 kg, ứng với 2/5 số cà chua. Hỏi bác nông dân đã mang bao nhiêu kilôgam cà chua ra chợ bán?

Trả lời:

Bác nông dân đã mang số kilôgam cà chua ra chợ bán là: $20 : \frac{2}{5} = 20 . \frac{5}{2} = 10.5 = 50$ (kg)Vậy bác nông dân đã mang 50 kilôgam cà chua ra chợ bán.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Câu hỏi:

Trả lời:

Bài liên quan:

Leave a Comment Hủy