Trong không gian Oxyz, cho hai mặt phẳng -mx + 3y + 2z + m – 6 = 0 và -2x + (5m + 1)y + (m + 3)z – 10 = 0. Hai mặt phẳng này cắt nhau khi và chỉ khi:

Câu hỏi:

Trong không gian Oxyz, cho hai mặt phẳng -mx + 3y + 2z + m – 6 = 0 và -2x + (5m + 1)y + (m + 3)z – 10 = 0. Hai mặt phẳng này cắt nhau khi và chỉ khi:

A. m ≠ -4

B. m ≠ -6/5

C. m ≠ 1

Đáp án chính xác

D. Mọi m

Trả lời:

Đáp án C
Gọi hai mặt phẳng đã cho lần lượt là (P) và (Q). Ta có

Hai vectơ này song song khi và chỉ khi m – 6 $\ne$ -10 hay m $\ne$-4 và tồn tại một số thực k sao cho

(thỏa mãn)
Từ đó suy ra hai mặt phẳng (P) và (Q) cắt nhau khi và chỉ khi hai vectơ pháp tuyến của chúng không song song, điều đó tương đương với m khác 1.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Trong không gian Oxyz, cho hai vectơ u→ = (-1; 3; 4), v→ = (2; -1; 5). Tích có hướng của hai vectơ u→ và v→ là:
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, cho hai vectơ $\overrightarrow{\mathrm{u}}$ = (-1; 3; 4), $\overrightarrow{\mathrm{v}}$ = (2; -1; 5). Tích có hướng của hai vectơ $\overrightarrow{\mathrm{u}}$ và $\overrightarrow{\mathrm{v}}$ là:

   A. $\left[\overrightarrow{\mathrm{u}},\overrightarrow{\mathrm{v}}\right]=\left(19;13;–5\right)$

   Đáp án chính xác

   B. $\left[\overrightarrow{\mathrm{u}},\overrightarrow{\mathrm{v}}\right]=\left(19;–13;–5\right)$

   C. $\left[\overrightarrow{\mathrm{u}},\overrightarrow{\mathrm{v}}\right]=\left(–19;13;–5\right)$

   D. $\left[\overrightarrow{\mathrm{u}},\overrightarrow{\mathrm{v}}\right]=\left(19;13;5\right)$

   Trả lời:

   Đáp án AHai vectơ $\overrightarrow{\mathrm{u}}$ = (-1; 3; 4), $\overrightarrow{\mathrm{v}}$ = (2; -1; 5)Thì tích có hướng của hai vectơ $\overrightarrow{\mathrm{u}}$ và $\overrightarrow{\mathrm{v}}$ là:[$\overrightarrow{\mathrm{u}}$,$\overrightarrow{\mathrm{v}}$] = (19; 13; -5)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:

   A. $\overrightarrow{{\mathrm{n}}_{\mathrm{p}}}=\left(2;5;–4\right)$

   B. $\overrightarrow{{\mathrm{n}}_{\mathrm{p}}}=\left(2;–5;4\right)$

   C. $\overrightarrow{{\mathrm{n}}_{\mathrm{p}}}=\left(–2;–5;4\right)$

   D. $\overrightarrow{{\mathrm{n}}_{\mathrm{p}}}=\left(2;–5;–4\right)$

   Đáp án chính xác

   Trả lời:

   Đáp án DTừ giả thiết ta suy ra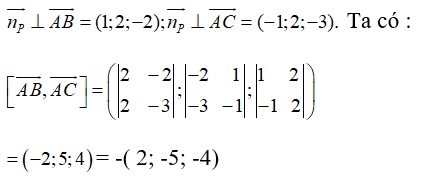Từ đó suy ra $\overrightarrow{{\mathrm{n}}_{\mathrm{p}}}$ = (2; -5; -4) là một vectơ pháp tuyến của (P)

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)

   A. x – y – 1 = 0

   Đáp án chính xác

   B. x – y + 1 = 0

   C. x + z – 2 = 0

   D. x + y – 1 = 0

   Trả lời:

   Đáp án ATừ giả thiết ta suy ra: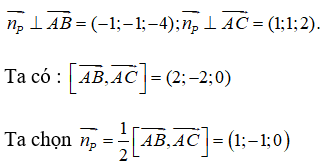Từ đó suy ra phương trình của mặt phẳng (P) là: 1(x – 1) – 1(y – 0) = 0 ⇔ x – y – 1 = 0

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y – 3z = 0 đồng thời (P) song song với trục Oz
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y – 3z = 0 đồng thời (P) song song với trục Oz

   A. x + y – 3 = 0

   B. x – y – 1 = 0

   Đáp án chính xác

   C. 2x + y + 3z – 1 = 0

   D. x – y + 1 = 0

   Trả lời:

   Đáp án BTừ giả thiết ta suy ra: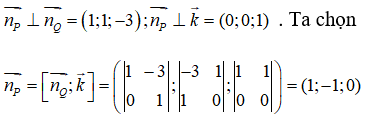Mặt khác mặt phẳng (P) đi qua điểm A(2;1;3) nên ta có phương trình của mặt phẳng (P) là: 1(x- 2) – 1(y – 1) = 0 ⇔ x – y – 1 = 0

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(2;6;-3) và vuông góc với hai mặt phẳng (Oxy), (Oyz) là:
   
   

   Câu hỏi:
   

   Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(2;6;-3) và vuông góc với hai mặt phẳng (Oxy), (Oyz) là:

   A. 2x – 4 = 0

   B. y – 6 = 0

   Đáp án chính xác

   C. z + 3 = 0

   D. 2x – 6y – 3z – 49 = 0

   Trả lời:

   Đáp án B
   Vì (P) vuông góc với hai mặt phẳng (Oxy), (Oyz) và (Oxy) $\cap$(Oyz) = Oy nên ta có (P) $\perp$ Oy => $\overrightarrow{{\mathrm{n}}_{\mathrm{p}} }=\overrightarrow{ \mathrm{j}}$ = (0; 1; 0)
   Từ đó suy ra phương trình của mặt phẳng (P) là: 0(x – 2) + 1(y – 6 ) + 0(z + 3) = 0 ⇔ y – 6 = 0

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====