Câu hỏi:
Tìm tất cả các giá trị của tham số \(m\) để hàm số \(y = – {x^3} – 3{x^2} + mx + 2\) có cực đại và cực tiểu?
A.\(m \ge 3.\)
B.\(m >- 3.\)
Đáp án chính xác
C.\(m >3.\)
D. \(m \ge – 3.\)
Trả lời:
Ta có \(y’ = – 3{x^2} – 6x + m.\) Hàm số có cực đại và cực tiểu khi và chỉ khi \(y’ = 0\) có hai nghiệm phân biệt \( \Leftrightarrow \Delta ‘ >0 \Leftrightarrow 9 + 3m >0 \Leftrightarrow m >- 3.\)
Đáp án B
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đường cong hình sau là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số nào?
Câu hỏi:
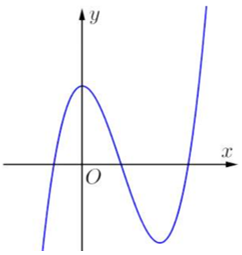
Đường cong hình sau là đồ thị của một trong bốn hàm số được cho dưới đây, hỏi đó là hàm số nào?
A.\(y = – {x^3} + 3{x^2} + 2.\)
B.\(y = {x^3} – 3{x^2} + 2.\)
Đáp án chính xác
C.\(y = {x^4} + 3{x^2} + 2.\)
D. \(y = {x^4} – 3{x^2} + 2.\)
Trả lời:
Ta thấy đồ thị như hình vẽ là đồ thị của hàm số bậc ba \(y = a{x^3} + b{x^2} + cx + d\) nên loại C, D.
Dựa vào đồ thị ta có \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) nên \(a >0\) suy ra loại A.
Vậy ta chọn đáp án B.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho khối lăng trụ đều \(ABC.A'B'C'\) có cạnh đáy và cạnh bên cùng bằng \(a.\) Tính thể tích của khối lăng trụ đó theo \(a.\)
Câu hỏi:
Cho khối lăng trụ đều \(ABC.A’B’C’\) có cạnh đáy và cạnh bên cùng bằng \(a.\) Tính thể tích của khối lăng trụ đó theo \(a.\)
A.\(\frac{{{a^3}\sqrt 3 }}{4}.\)
Đáp án chính xác
B.\(\frac{{{a^3}\sqrt 6 }}{4}.\)
C.\(\frac{{{a^3}\sqrt 3 }}{{12}}.\)
D. \(\frac{{{a^3}\sqrt 6 }}{{12}}.\)
Trả lời:
Vì \(ABC.A’B’C’\) là khối lăng trụ đều nên có đáy \(ABC\) là tam giác đều và chiều cao \(AA’ = a.\)
Khi đó thể tích của khối lăng trụ đã cho là \(V = AA’.{S_{ABC}} = a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{4}\) (đvtt).
Đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tính diện tích xung quanh \(S\) của hình nón có bán kính đáy \(r = 4\) và chiều cao \(h = 3.\)
Câu hỏi:
Tính diện tích xung quanh \(S\) của hình nón có bán kính đáy \(r = 4\) và chiều cao \(h = 3.\)
A.\(S = 40\pi .\)
B.\(S = 12\pi .\)
C.\(S = 20\pi .\)
Đáp án chính xác
D. \(S = 10\pi .\)
Trả lời:
Độ dài đường sinh của hình nón \(l = \sqrt {{r^2} + {h^2}} = \sqrt {{4^2} + {3^2}} = 5.\)
Diện tích xung quanh của hình nón \(S = \pi rl = 4.5\pi = 20\pi .\)
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công sai \(d = 2.\) Tính \({u_9}.\)
Câu hỏi:
Cho cấp số cộng \(\left( {{u_n}} \right)\) có số hạng đầu \({u_1} = 3\) và công sai \(d = 2.\) Tính \({u_9}.\)
A.\({u_9} = 26.\)
B.\({u_9} = 19.\)
Đáp án chính xác
C.\({u_9} = 16.\)
D. \({u_9} = 29.\)
Trả lời:
Ta có \({u_9} = {u_1} + \left( {9 – 1} \right)d = 3 + 8.2 = 19.\)
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc?
Câu hỏi:
Có bao nhiêu cách sắp xếp 5 học sinh thành một hàng dọc?
A. 20.
B. 120.
Đáp án chính xác
C. 25.
D. \({5^3}.\)
Trả lời:
Mỗi cách sắp xếp 5 học sinh là một hoán vị của 5 phần tử.
Vậy có 5! = 120 cách sắp xếp 5 học sinh thành một hàng dọc.
Đáp án B====== **** mời các bạn xem câu tiếp bên dưới **** =====