Gọi S tập hợp các giá trị m để đồ thị hàm số y=x4−2m2x2+1 có 3 điểm cực trị tạo thành một tam giác vuông cân. Tổng bình phương các phần tử của S bằng

Câu hỏi:

Gọi S tập hợp các giá trị m để đồ thị hàm số $y=x^4-2m^2{x}^2+1$ có 3 điểm cực trị tạo thành một tam giác vuông cân. Tổng bình phương các phần tử của S bằng

A. 2                             

Đáp án chính xác

B. 4                             

C. 8                             

D. 6

Trả lời:

Ta có $y=x^4-2m^2{x}^2+1\Rightarrow y‘=4x^3-4m^{2}x$
$y‘=0\iff 4x^3-4m^{2}x=0\iff 4x\left(x^2-m^2\right)=0\iff \left[\begin{array}{l}x=0\\ x^2=m^2\end{array}\right..$
 
Để hàm số có 3 điểm cực trị thì phương trình y’ = 0 phải có 3 nghiệm phân biệt $\Rightarrow m\ne 0.$
Khi đó ta có $y‘=0\iff \left[\begin{array}{l}x=0\Rightarrow y=1\\ x=m\Rightarrow y=-m^4+1\\ x=-m\Rightarrow y=-m^4+1\end{array}\right..$
Suy ra các điểm cực trị của hàm số đã cho là: $A\left(0;1\right);B\left(m;-m^4+1\right);C\left(-m;-m^4+1\right).$
Vì $A\in Oy,B,C$ đối xứng nhau qua Oy nên $\Delta ABC$ cân tại A, do đó để ABC là tam giác vuông thì phải vuông tại $A\Rightarrow \overrightarrow{AB}.\overrightarrow{AC}=0.$
Ta có: $\left\{\begin{array}{l}\overrightarrow{AB}=\left(m;-m^4\right)\\ \overrightarrow{AC}=\left(-m;-m^4\right)\end{array}\right.\Rightarrow \overrightarrow{AB}.\overrightarrow{AC}=0\iff -m^2+m^8=0\iff m^2\left(m^6-1\right)=0\iff \left[\begin{array}{l}m=0\\ m=\pm 1\end{array}\right.$
Có ABC là tam giác vuông cân tại A nên $BC=AB\sqrt{2}\Rightarrow 4m^2=2\left(m^2+m^8\right)\Rightarrow \left[\begin{array}{l}m=0\left(tm\right)\\ m=\pm 1\left(tm\right)\end{array}\right..$
Vậy $S=\left\{-1;1\right\}\Rightarrow$ Tổng bình phương các phần tử của S bằng 2.
Chọn A.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hàm số y = f(x) có bảng biến thiên như sau: Hàm số y = f(x) đồng biến trên khoảng nào sau đây? 
   
   

   Câu hỏi:
   

   Cho hàm số y = f(x) có bảng biến thiên như sau:
   
   Hàm số y = f(x) đồng biến trên khoảng nào sau đây? 

   A. $\left(3;+\infty \right)$

   Đáp án chính xác

   B. (1; 3)

   C. $\left(-\infty ;4\right)$

   D. $\left(0;+\infty \right)$

   Trả lời:

   Hàm số đồng biến trên khoảng là $\left(-\infty ;1\right)$ và $\left(3;+\infty \right)$.
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y = f(x) có đồ thị như hình vẽ. Mệnh đề nào dưới đây đúng? 
   
   

   Câu hỏi:
   

   Cho hàm số y = f(x) có đồ thị như hình vẽ.
   
   Mệnh đề nào dưới đây đúng? 

   A. Hàm số đạt cực đại tại x = -1 và x = 1       

   B. Hàm số đạt cực tiểu tại x = 0 

   C. Hàm số đạt cực đại tại x = 0                       

   Đáp án chính xác

   D. Hàm số đạt cực đại tại x = 1

   Trả lời:

   Ta có đồ thị hàm số có 3 cực trị trong đó có 1 cực đại tại x = 0 và 2 cực tiểu tại x = -1; x = 1.
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Đường cong ở hình bên dưới là đồ thị của hàm số y=ax+bcx+d với a, b, c, d là các số thực. Giá trị nhỏ nhất của hàm số trên đoạn [-1; 0] là
   
   

   Câu hỏi:
   

   Đường cong ở hình bên dưới là đồ thị của hàm số $y=\frac{ax+b}{cx+d}$ với a, b, c, d là các số thực. Giá trị nhỏ nhất của hàm số trên đoạn [-1; 0] là
   

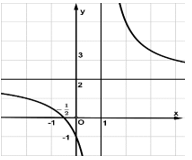
   A. -1                           

   B. 1                             

   C. 0                             

   D. 2

   Đáp án chính xác

   Trả lời:

   Ta thấy trên đoạn [-1;0] đồ thị hàm số hướng xuống hay hàm số nghịch biến nên $\underset{\left[-1;0\right]}{\min }y=y\left(0\right)=-1.$
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Khẳng định nào đúng về tính đơn điệu của hàm số y=x+2x−1?
   
   

   Câu hỏi:
   

   Khẳng định nào đúng về tính đơn điệu của hàm số $y=\frac{x+2}{x-1}?$

   A. Hàm số nghịch biến trên các khoảng $\left(-\infty ;1\right)$ và $\left(1;+\infty \right).$

   B. Hàm số đồng biến trên các khoảng $\left(-\infty ;1\right)\cup \left(1;+\infty \right).$

   C. Hàm số đồng biến trên các khoảng $\left(-\infty ;1\right)$ và $\left(1;+\infty \right).$

   Đáp án chính xác

   D. Hàm số nghịch biến trên các khoảng $\left(-\infty ;–1\right)$ và $\left(–1;+\infty \right).$

   Trả lời:

   Ta thấy: $y=\frac{x+2}{x-2}\Rightarrow y‘=\frac{-3}{{\left(x-1\right)}^2}<0\forall x\ne 1$ nên hàm số nghịch biến trên các khoảng $\left(-\infty ;1\right),\left(1;+\infty \right).$
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho hàm số y=x4−2×2+2021. Điểm cực đại của hàm số là:
   
   

   Câu hỏi:
   

   Cho hàm số $y=x^4-2x^2+2021.$ Điểm cực đại của hàm số là:

   A. x = 0

   Đáp án chính xác

   B. x = 2021

   C. x = -1

   D. x = 1

   Trả lời:

   Hàm số $y=x^4-2x^2+2021$ có điểm cực đại thỏa mãn $\left\{\begin{array}{l}y‘=4x^3-4x=0\\ y“=12x^2-4<0\end{array}\right.\iff x=0.$
   Chọn A.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====