Gọi A, B là hai điểm trong mặt phẳng phức theo thứ tự biểu diễn các số phức z1, z2 khác 0 thỏa mãn đẳng thức z12 + z22 – z1z2 = 0, khi đó tam giác OAB (O là gốc tọa độ)

Câu hỏi:

Gọi A, B là hai điểm trong mặt phẳng phức theo thứ tự biểu diễn các số phức $z_1, z_2$ khác 0 thỏa mãn đẳng thức $z_1^2 + z_2^2 – z_1{z}_2$ = 0, khi đó tam giác OAB (O là gốc tọa độ)

A. Là tam giác đều.

Đáp án chính xác

B. Là tam giác vuông.

C. Là tam giác cân, không đều.

D. Là tam giác tù.

Trả lời:

Đáp án A.
Cách 1: Ta có: 


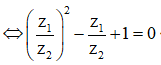
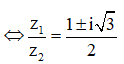
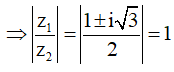
mặt khác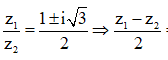 
Do đó tam giác OAB là tam giác đều. 
Cách 2: Chọn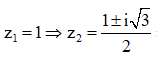 

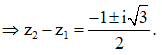
====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.z¯= 1 và |z – 3 + i|. Tìm số phần tử của S
   
   

   Câu hỏi:
   

   Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.$\overline{z}$= 1 và |z – $\sqrt{3}$ + i|. Tìm số phần tử của S

   A. 1.

   Đáp án chính xác

   B. 2.

   C. 3.

   D. 4

   Trả lời:

   Đáp án A
   Đặt z=x+yi
   Ta có  suy ra tập biểu diễn số phức z là đường tròn tâm M(0;0) bán kính R=1
   (m > 0) suy ra tập biểu diễn số phức z là đường tròn tâm N($\sqrt{3}$;1) bán kính r=m
   Để tồn tại duy nhất số phức z thì 2 đường tròn phải tiếp xúc với nhau suy ra MN=R+r
   Vậy tập S chỉ có 1 giá trị của m

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Gọi z1, z2 là hai nghiệm của phương trình z2 – 2z + 2 = 0, (z∈ℂ). Tính giá trị của biểu thức P = 2|z1 + z2| + |z1- z2| 
   
   

   Câu hỏi:
   

   Gọi $z_1, z_2$ là hai nghiệm của phương trình $z^2$ – 2z + 2 = 0, (z$\in \mathrm{ℂ}$). Tính giá trị của biểu thức P = 2|$z_1 +\hspace{0.17em}{z}_2$| + |$z_1–\hspace{0.17em}{z}_2$| 

   A. P = 6

   Đáp án chính xác

   B. P = 3

   C. P = $2\sqrt{2}$ + 2

   D. P = $\sqrt{2}$ + 4

   Trả lời:

   Đáp án A
   
   => P = 6

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho số phức z thỏa mãn (3-4i)z – 4z = 8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?
   
   

   Câu hỏi:
   

   Cho số phức z thỏa mãn (3-4i)z – $\frac{4}{z}$ = 8. Trên mặt phẳng tọa độ, khoảng cách từ gốc tọa độ đến điểm biểu diễn số phức z thuộc tập nào?

   $A. (\frac{9}{4};+\infty )$

   $B. (\frac{1}{4};\frac{5}{4})$

   $C. (0;\frac{1}{4})$

   $D. (\frac{1}{2};\frac{9}{4})$

   Đáp án chính xác

   Trả lời:

   Đáp án D
   Ta có (3-4i)z – $\frac{4}{z}$ = 8 
   Lấy môđun hai vế của (*) và sử dụng công thức ta được
   
   
   Gọi M(x;y) là điểm biểu diễn số phức z. Khi đó OM = 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4.  Cho số phức z thỏa mãn z(2-i) + 13i = 1. Tính mô đun của số phức z.
   
   

   Câu hỏi:
   

    Cho số phức z thỏa mãn z(2-i) + 13i = 1. Tính mô đun của số phức z.

   A. |z| = $\sqrt{34}$

   Đáp án chính xác

   B. |z| = 34

   C. |z| = $\frac{5\sqrt{34}}{3}$

   D. |z| = $\frac{\sqrt{34}}{3}$

   Trả lời:

   Đáp án A
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tìm số phức z thỏa mãn |z-2| = |z| và |z+1|(z¯-i) là số thực.
   
   

   Câu hỏi:
   

   Tìm số phức z thỏa mãn |z-2| = |z| và |z+1|($\overline{z}$-i) là số thực.

   A. z = 1 – 2i

   Đáp án chính xác

   B. z = -1 – 2i

   C. z = 2 – i

   D. z = 1 + 2i

   Trả lời:

   Đáp án A
   Đặt z = a + bi; 
   Mặt khác  là số thực, suy ra
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====