Câu hỏi:
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(2a,\) cạnh bên bằng \(3a.\) Tính thể tích \(V\) của hình chóp đã cho.
A.\(V = 4\sqrt 7 {a^3}.\)
B. \(V = \frac{4}{3}{a^3}.\)
C.\(V = \frac{{4\sqrt 7 {a^3}}}{3}.\)
Đáp án chính xác
D. \(V = \frac{{4\sqrt 7 {a^3}}}{9}.\)
Trả lời:
Đáp án C.
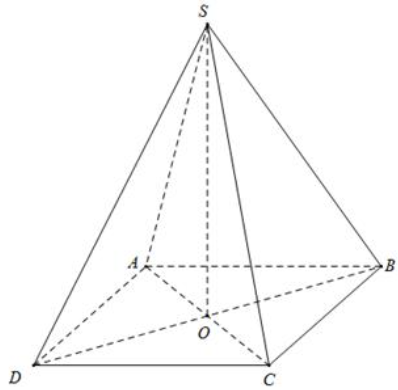
Gọi \(O = AC \cap BD.\)
Vì \(S.ABCD\) là hình chóp tứ giác đều nên \(SO \bot \left( {ABCD} \right).\)
Theo bài ra ta có: \(OA = \frac{1}{2}AC = a\sqrt 2 .\)
Xét tam giác \(SOA\) vuông tại \(O\) ta có: \(SO = \sqrt {S{A^2} – O{A^2}} = \sqrt {{{\left( {3a} \right)}^2} – {{\left( {a\sqrt 2 } \right)}^2}} = a\sqrt 7 .\)
Diện tích hình vuông \(ABCD\) bằng: \({S_{ABCD}} = {\left( {2a} \right)^2} = 4{a^2}.\)
Thể tích của khối chóp \(S.ABCD\) bằng: \({V_{S.ABCD}} = \frac{1}{3}.SO.{S_{ABCD}} = \frac{1}{3}.a\sqrt 7 .4{a^2} = \frac{{4\sqrt 7 {a^3}}}{3}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(a,b\) là hai số thực dương bất kì. Mệnh đề nào dưới đây đúng?
Câu hỏi:
Cho \(a,b\) là hai số thực dương bất kì. Mệnh đề nào dưới đây đúng?
A.\(\ln \left( {a{b^2}} \right) = \ln a + {\left( {\ln b} \right)^2}.\)
B.\(\ln \left( {ab} \right) = \ln a.\ln b.\)
C.\(\ln \left( {a{b^2}} \right) = \ln a + 2\ln b.\)
Đáp án chính xác
D. \(\ln \frac{a}{b} = \frac{{\ln a}}{{\ln b}}.\)
Trả lời:
Đáp án C.
\(\ln \left( {a{b^2}} \right) = \ln a + \ln {b^2} = \ln a + 2\ln b.\) Do đó câu A sai.
\(\ln \left( {ab} \right) = \ln a + \ln b\) nên câu B sai.
\(\ln \frac{a}{b} = \ln a – \ln b\) nên câu D sai.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên ở hình vẽ. Hàm số có giá trị cực tiểu bằng
Câu hỏi:
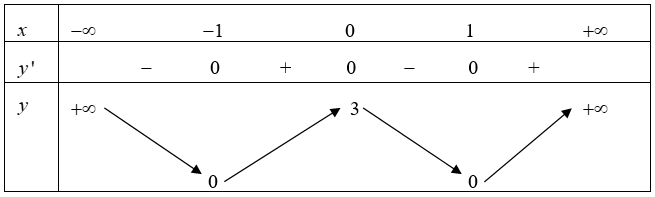
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên ở hình vẽ. Hàm số có giá trị cực tiểu bằng
A.1.
B.3.
C.\( – 1.\)
D. 0.
Đáp án chính xác
Trả lời:
Đáp án D.
Dựa vào bảng biến thiên ta thấy \(y’\) đổi dấu từ âm sang dương khi \(x\) đi qua \({x_1} = – 1\) và \({x_3} = 1.\)
Mặt khác \(y\left( { – 1} \right) = y\left( 1 \right) = 0.\)
Vậy giá trị cực tiểu của hàm số là 0.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho tập hợp \(A\) có 26 phần tử. Hỏi \(A\) có bao nhiêu tập con gồm 6 phần tử?
Câu hỏi:
Cho tập hợp \(A\) có 26 phần tử. Hỏi \(A\) có bao nhiêu tập con gồm 6 phần tử?
A.\(A_{26}^6.\)
B. 26.
C.\({P_6}.\)
D. \(C_{26}^6.\)
Đáp án chính xác
Trả lời:
Đáp án D.
Số các tập con bằng số tổ hợp chập 6 của 26: \(C_{26}^6.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong mặt phẳng tọa độ \(Oxy,\) ảnh của điểm \(M\left( { – 6;1} \right)\) qua phép vị tự tâm \(O\) tỷ số \(k = 2\) là
Câu hỏi:
Trong mặt phẳng tọa độ \(Oxy,\) ảnh của điểm \(M\left( { – 6;1} \right)\) qua phép vị tự tâm \(O\) tỷ số \(k = 2\) là
A.\(M’\left( {12; – 2} \right).\)
B.\(M’\left( {1; – 6} \right).\)
C.\(M’\left( { – 12;2} \right).\)
Đáp án chính xác
D. \(M’\left( { – 6;1} \right).\)
Trả lời:
Đáp án C.
Phép vị tự tâm \(O\left( {0;0} \right)\) tỉ số \(k = 2\) biến điểm \(M\left( { – 6;1} \right)\) thành điểm \(M’\left( {x’;y’} \right)\) thỏa mãn:
\(\left\{ \begin{array}{l}x’ = – 6.2\\y’ = 1.2\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x’ = – 12\\y’ = 2\end{array} \right. \Rightarrow M’\left( { – 12;2} \right)\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
Câu hỏi:
Hàm số nào dưới đây nghịch biến trên tập xác định của nó?
A.\(y = \ln x.\)
B.\(y = {\log _{\frac{2}{3}}}x.\)
Đáp án chính xác
C.\(y = \log x.\)
D. \(y = {\log _{\frac{5}{2}}}x.\)
Trả lời:
Đáp án B.
Hàm số \(y = {\log _a}x\) nghịch biến trên tập xác định khi \(0 < a < 1.\)
Vậy hàm số \(y = {\log _{\frac{2}{3}}}x\) nghịch biến trên tập xác định.====== **** mời các bạn xem câu tiếp bên dưới **** =====