Câu hỏi:
Cho hàm số \(y = {x^4} – 2m{x^2} + m,\) có đồ thị \(\left( C \right)\) với \(m\) là tham số thực. Gọi \(A\) là điểm thuộc đồ thị \(\left( C \right)\) có hoành độ bằng 1. Tìm \(m\) để tiếp tuyến \(\Delta \) với đồ thị \(\left( C \right)\) tại \(A\) cắt đường tròn tạo thành một dây cung có độ dài nhỏ nhất.
A.\( – \frac{{15}}{{16}}.\)
B. \(\frac{{15}}{{16}}.\)
C.\( – \frac{{17}}{{16}}.\)
D.\(\frac{{17}}{{16}}.\)
Đáp án chính xác
Trả lời:
\(y’ = 4{x^3} – 4mx,y’\left( 1 \right) = 4 – 4m,y\left( 1 \right) = 1 – m.\) Ta có điểm \(A\left( {1;1 – m} \right).\)
Phương trình tiếp tuyến của đồ thị \(\left( C \right)\) tại điểm \(A\left( {1;1 – m} \right)\) là
\(y = y’\left( 1 \right)\left( {x – 1} \right) + 1 – m \Rightarrow y = \left( {4 – 4m} \right)\left( {x – 1} \right) + 1 – m \Rightarrow y = \left( {4 – 4m} \right)x + 3m – 3\) suy ra phương trình tiếp tuyến  là \(\left( {4 – 4m} \right)x – y + 3m – 3 = 0.\)
là \(\left( {4 – 4m} \right)x – y + 3m – 3 = 0.\)
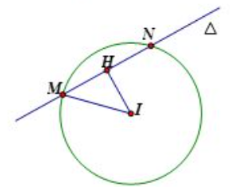
\(MN = 2MH = 2\sqrt {I{M^2} – I{H^2}} = 2\sqrt {4 – I{H^2}} \).
Ta có \(MN\) nhỏ nhất khi \(IH\) lớn nhất. Ta có \(IH = d\left( {I,\Delta } \right) = \frac{{\left| m \right|}}{{\sqrt {{{\left( {4 – 4m} \right)}^2} + 1} }}.\)
\(IH\) lớn nhất khi \(I{H^2}\) lớn nhất hay \(\frac{{{m^2}}}{{16{m^2} – 32m + 17}}\) lớn nhất.
Xét hàm \(f\left( m \right) = \frac{{{m^2}}}{{16{m^2} – 32m + 17}}\) suy ra \(f’\left( m \right) = \frac{{ – 32{m^2} + 34m}}{{{{\left( {16{m^2} – 32m + 17} \right)}^2}}}.\)
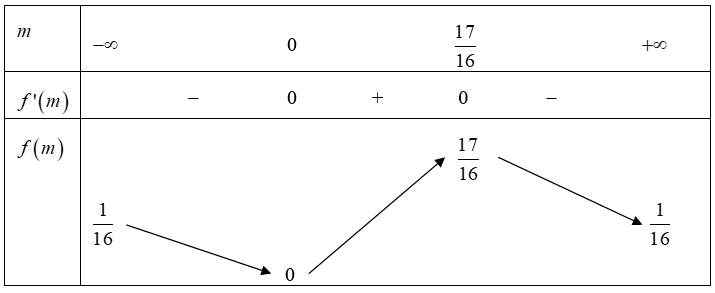
Từ bảng ta có \(IH\) lớn nhất khi \(m = \frac{{17}}{{16}}.\) Vậy dây cung \(MN\)nhỏ nhất khi \(m = \frac{{17}}{{16}}.\)
Đáp án D
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho giới hạn \(\mathop {\lim }\limits_{x \to – 4} \frac{{{x^2} + 3x – 4}}{{{x^2} + 4x}} = \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính giá trị biểu thức \({a^2} – {b^2}.\)
Câu hỏi:
Cho giới hạn \(\mathop {\lim }\limits_{x \to – 4} \frac{{{x^2} + 3x – 4}}{{{x^2} + 4x}} = \frac{a}{b}\) với \(\frac{a}{b}\) là phân số tối giản. Tính giá trị biểu thức \({a^2} – {b^2}.\)
A. \( – 9\).
B. 41.
C. 9.
Đáp án chính xác
D. 14.
Trả lời:
\(\mathop {\lim }\limits_{x \to – 4} \frac{{{x^2} + 3x – 4}}{{{x^2} + 4x}} = \mathop {\lim }\limits_{x \to – 4} \frac{{\left( {x – 1} \right)\left( {x + 4} \right)}}{{x\left( {x + 4} \right)}} = \mathop {\lim }\limits_{x \to – 4} \frac{{x – 1}}{x} = \frac{5}{4}.\)
\( \Rightarrow a = 5;b = 4\)
\( \Rightarrow {a^2} – {b^2} = 25 – 16 = 9.\)
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right),\) biết \(AB = AC = a,BC = a\sqrt 3 .\) Tính góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right).\)
Câu hỏi:
Cho hình chóp \(S.ABC\) có cạnh \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right),\) biết \(AB = AC = a,BC = a\sqrt 3 .\) Tính góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SAC} \right).\)
A.\({45^0}.\)\(\angle SCA\)
B.\({30^0}.\)
C.
Đáp án chính xác
D. \({90^0}.\)
Trả lời:

\(\left\{ \begin{array}{l}SA = \left( {SAB} \right) \cap \left( {SAC} \right)\\AB \bot SA\left( {SA \bot \left( {ABC} \right)} \right)\\AC \bot SA\left( {SA \bot \left( {ABC} \right)} \right)\\AB \subset \left( {SAB} \right)\\AC \subset \left( {SAC} \right)\end{array} \right. \Rightarrow \left( {\left( {SAB} \right),\left( {SAC} \right)} \right) = \left( {AB,AC} \right)\)
\(\Delta ABC\) có: \(\cos \widehat A = \frac{{A{B^2} + A{C^2} – B{C^2}}}{{2.AB.AC}} = – \frac{1}{2} \Rightarrow \widehat A = {120^0}.\)
\( \Rightarrow \left( {\left( {SAB} \right),\left( {SAC} \right)} \right) = {60^0}.\)
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đường cong trong hình vẽ bên là đồ thị của hàm số nào
Câu hỏi:
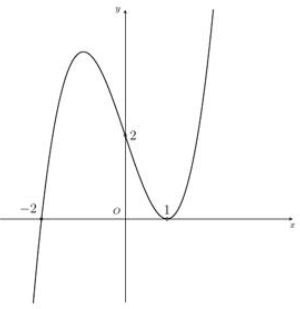
Đường cong trong hình vẽ bên là đồ thị của hàm số nào
A.\(y = \left( {x – 1} \right){\left( {x – 2} \right)^2}.\)
B.\(y = \left( {x – 1} \right){\left( {x + 2} \right)^2}.\)
C.\(y = {\left( {x – 1} \right)^2}\left( {x + 2} \right).\)
Đáp án chính xác
D. \(y = {\left( {x + 1} \right)^2}\left( {x + 2} \right).\)
Trả lời:
Do đồ thị hàm số tiếp xúc với trục hoành tại điểm \(\left( {1;0} \right)\) nên đường cong là đồ thị của hàm số \(y = {\left( {x – 1} \right)^2}\left( {x + 2} \right).\)
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SD = \frac{{3a}}{2},\) hình chiếu vuông góc của \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm của cạnh \(AB.\) Tính theo \(a\) thể tích khối chóp \(S.ABCD.\)
Câu hỏi:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SD = \frac{{3a}}{2},\) hình chiếu vuông góc của \(S\) trên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm của cạnh \(AB.\) Tính theo \(a\) thể tích khối chóp \(S.ABCD.\)
A. \(\frac{{{a^3}}}{4}.\)
B.\(\frac{{2{a^3}}}{3}.\)
C.\(\frac{{{a^3}}}{3}.\)
Đáp án chính xác
D. \(\frac{{{a^3}}}{2}.\)
Trả lời:

Gọi \(H\) là trung điểm cạnh \(AB.\) Khi đó \(SH \bot \left( {ABCD} \right).\)
Tam giác \(AHD\) vuông tại \(H\) có \(D{H^2} = A{H^2} + A{D^2} = \frac{{{a^2}}}{4} + {a^2} = \frac{{5{a^2}}}{4}.\)
Tam giác \(SHD\) vuông tại \(H\)có \(S{H^2} = S{D^2} – D{H^2} = \frac{{9{a^2}}}{4} – \frac{{5{a^2}}}{4} = {a^2} \Rightarrow SH = a.\)
Vậy \({V_{S.ABCD}} = \frac{1}{3}a.{a^2} = \frac{{{a^3}}}{3}\) (đvtt).
Đáp án C====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm thuộc đồ thị hàm số \(y = {\log _3}x.\) Tìm điều kiện của \({x_0}\) để điểm \(M\) nằm phía trên đường thẳng \(y = 2.\)
Câu hỏi:
Gọi \(M\left( {{x_0};{y_0}} \right)\) là điểm thuộc đồ thị hàm số \(y = {\log _3}x.\) Tìm điều kiện của \({x_0}\) để điểm \(M\) nằm phía trên đường thẳng \(y = 2.\)
A.\({x_0} >9.\)
Đáp án chính xác
B.\({x_0} >0.\)
C.\({x_0} < 2.\)
</>D. \({x_0} >2.\)
Trả lời:
Điểm \(M\) nằm phía trên đường thẳng \(y = 2\) khi \({y_0} >2 \Leftrightarrow {\log _3}{x_0} >2 \Leftrightarrow {x_0} >9.\)
Đáp án A====== **** mời các bạn xem câu tiếp bên dưới **** =====