Cho hàm số y = f(x) = ax4 + bx2 + c (a > 0) có đồ thị (C), đồ thị hàm số y = f’(x). Đồ thị hàm số y = f(x)  tiếp xúc với trục hoành tại hai điểm. Tính diện tích  của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?

Câu hỏi:

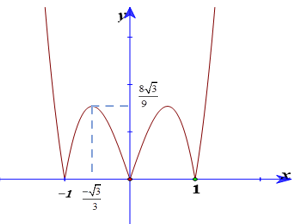
Cho hàm số y = f(x) = ax⁴ + bx² + c (a > 0) có đồ thị (C), đồ thị hàm số y = f’(x). Đồ thị hàm số y = f(x)  tiếp xúc với trục hoành tại hai điểm. Tính diện tích  của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?

A. $\frac{7}{15}$

B. $\frac{8}{15}$

C. $\frac{14}{15}$

D. $\frac{16}{15}$

Đáp án chính xác

Trả lời:

+ Từ đồ thị của hàm số  và a > 0 ta dễ dàng có được đồ thị hàm số y = f’(x)  như sau:
Ta có : f’(x) = 4ax³ + 2bx
 Đồ thị hàm số y = f’(x)  đi qua 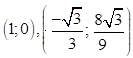 ta tìm được a = 1 và b = -2
Suy ra hàm số đã cho có dạng: f(x) = x⁴ – 2x² + d và f’(x) = 4x³ – 4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x = 0; x = 1; x = -1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) = 1  suy ra 1= 0 – 2.0 + d nên d = 1
Vậy hàm số cần tìm là: y = x⁴ – 2x² + 1  
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x⁴ – 2x² + 1 = 0 nên x = ±1

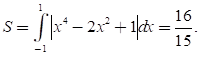
Chọn D.
 

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho hàm số  y=2x-1x+1 có đồ thị (C) . Biết khoảng cách từ  I(-1; 2) đến tiếp tuyến của (C)  tại M là lớn nhất thì tung độ của điểm M  nằm ở góc phần tư thứ hai, gần giá trị nào nhất?
   
   

   Câu hỏi:
   

   Cho hàm số  $y=\frac{2x–1}{x+1}$ có đồ thị (C) . Biết khoảng cách từ  I(-1; 2) đến tiếp tuyến của (C)  tại M là lớn nhất thì tung độ của điểm M  nằm ở góc phần tư thứ hai, gần giá trị nào nhất?

   A.3e

   B.2e

   C.e

   Đáp án chính xác

   D.4e

   Trả lời:

   +) Ta có $y‘=\frac{3}{{\left(x+1\right)}^2}$; I(-1; 2).
   +) Gọi $M\left(x_0;\frac{2x_0–1}{x_0+1}\right)\in \left(C\right), x_0\ne –1, y_0=\frac{2x_0–1}{x_0+1}>0.$
   Phương trình tiếp tuyến tại M  là
   
   +)
   +) Dấu  xảy ra khi và chỉ khi
   
   Tung độ này gần với giá trị e nhất trong các đáp án.
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hàm số y=2x-3x-2 có đồ thị (C) . Biết tiếp tuyến tại M  của (C)  cắt hai tiệm cận của (C)  tại A; B sao cho AB  ngắn nhất. Khi đó, độ dài lớn nhất của vectơ OM→ gần giá trị nào nhất ?
   
   

   Câu hỏi:
   

   Cho hàm số $y=\frac{2x–3}{x–2}$ có đồ thị (C) . Biết tiếp tuyến tại M  của (C)  cắt hai tiệm cận của (C)  tại A; B sao cho AB  ngắn nhất. Khi đó, độ dài lớn nhất của vectơ $\overrightarrow{OM}$ gần giá trị nào nhất ?

   A. 7.

   B. 5.

   C. 6.

   D. 4.

   Đáp án chính xác

   Trả lời:

   
   
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Viết phương trình tiếp tuyến d của đồ thị (C) :  y=2x+1x+1 biết d  cách đều  điểm A( 2; 4) và B( -4; -2).
   
   

   Câu hỏi:
   

   Viết phương trình tiếp tuyến d của đồ thị (C) :  $y=\frac{2x+1}{x+1}$ biết d  cách đều  điểm A( 2; 4) và B( -4; -2).

   A. $y=\frac{1}{4}x+\frac{1}{4}, y= x+3, y=x+1$

   B. $y=\frac{1}{4}x+\frac{5}{2}, y= x+5, y=x+1$

   C. $y=\frac{1}{4}x+\frac{5}{4}, y= x+4, y=x+1$

   D. $y=\frac{1}{4}x+\frac{5}{4}, y= x+5, y=x+1$

   Đáp án chính xác

   Trả lời:

   Gọi M( x₀; y₀) , $x_0\ne –1$  là tọa độ tiếp điểm của d và (C).
   Khi đó d có hệ số góc $y‘\left(x_0\right)=\frac{1}{{\left(x_0+1\right)}^2}$  và có phương trình là :
   
   Vì d  cách đều A: B nên d  đi qua trung điểm I( -1; 1) của AB  hoặc cùng phương với AB .
   TH1: d đi qua trung điểm I( -1; 1) , thì ta luôn có:
   ,
   phương trình này có nghiệm x₀= 1
   Với x₀= 1  ta có phương trình tiếp tuyến $d: \frac{1}{4}x+\frac{5}{4}$
   TH2: d cùng phương với AB , tức là d  và AB  có cùng hệ số góc, khi đó
   
   hay
    $\frac{1}{{\left(x_0+1\right)}^2}=1\iff x_0=–2 hoặc x_0=0$
   Với x₀ = -2  ta có phương trình tiếp tuyến d: y= x+ 5.
   Với x₀ =0   ta có phương trình tiếp tuyến d: y=x+ 1.
   Vậy, có 3 tiếp tuyến thỏa mãn đề bài:$y= \frac{1}{4}x+\frac{5}{4}$  , y= x+ 5, y=x+ 1
   Chọn D.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho hàm số y= 3x-4×3 có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?
   
   

   Câu hỏi:
   

   Cho hàm số y= 3x-4x³ có đồ thị (C). Từ điểm M(1;3) có thể kẻ được bao nhiêu tiếp tuyến với đồ thị hàm số (C) ?

   A. 0.

   B. 3.

   C. 2.

   Đáp án chính xác

   D. 1.

   Trả lời:

   + Đường thẳng đi qua M(1;3)  có hệ số góc k có dạng d: y=k(x-1)+3 .
   + d là tiếp tuyến của (C) khi và chỉ khi hệ sau có nghiệm:
    
   Thay (2) vào (1) ta được
   
    
   Vậy có 2 tiếp tuyến.
   Chọn C.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Qua điểm A(0; 2)  có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x4 – 2×2 + 2
   
   

   Câu hỏi:
   

   Qua điểm A(0; 2)  có thể kẻ được bao nhiêu tiếp tuyến với đồ thị của hàm số y = x⁴ – 2x² + 2

   A.2

   B.3

   Đáp án chính xác

   C.0

   D.1

   Trả lời:

   Gọi d  là tiếp tuyến của đồ thị hàm số đã cho.
   Vì $A\in d$ nên phương trình của d  có dạng: y = kx + 2
   Vì d tiếp xúc với đồ thị (C)  nên hệ
    có nghiệm
   Thay (2)  vào (1)  ta suy ra được 
   
   Chứng tỏ từ A có thể kẻ được 3 tiếp tuyến đến đồ thị (C)
   Chọn B.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====