Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f’\left( x \right) = {x^2}\left( {x – 2} \right)\left( {{x^2} – 6x + m} \right)\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu số nguyên m thuộc đoạn \(\left[ { – 2019;2019} \right]\) để hàm số \(g\left( x \right) = f\left( {1 – x} \right)\) nghịch biến trên khoảng \(\left( { – \infty ; – 1} \right)\)?
A. 2010.
B. 2012.
C. 2011.
Đáp án chính xác
D. 2009.
Trả lời:
Đáp án C
Phương pháp:
Hàm số nghịch biến trên \(\left( { – \infty ; – 1} \right)\) nếu \(g’\left( x \right) \le 0,\forall x \in \left( { – \infty ; – 1} \right)\).
Cách giải:
Ta có \(\begin{array}{l}g’\left( x \right) = – f’\left( {1 – x} \right) = – {\left( {1 – x} \right)^2}\left( {1 – x – 2} \right)\left[ {{{\left( {1 – x} \right)}^2} – 6\left( {1 – x} \right) + m} \right]\\ = – {\left( {1 – x} \right)^2}\left( { – 1 – x} \right)\left( {{x^2} + 4x + m – 5} \right) = {\left( {x – 1} \right)^2}\left( {x + 1} \right)\left( {{x^2} + 4x + m – 5} \right).\end{array}\)
Hàm số \(g\left( x \right)\) nghịch biến trên \(\left( { – \infty ; – 1} \right)\).
\(\begin{array}{l} \Leftrightarrow g’\left( x \right) \le 0,\forall x \in \left( { – \infty ; – 1} \right) \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} + 4x + m – 5} \right) \le 0,\forall x \in \left( { – \infty ; – 1} \right)\\ \Leftrightarrow {x^2} + 4x + m – 5 \ge 0,\forall x \in \left( { – \infty ; – 1} \right)\;\left( {{\rm{do}}\;x + 1 < 0,\forall x \in \left( { – \infty ; – 1} \right)} \right)\\ \Leftrightarrow h\left( x \right) = {x^2} + 4x – 5 \ge m\;\forall x \in \left( { – \infty ; – 1} \right) \Leftrightarrow – m \le \mathop {\min }\limits_{\left( { – \infty ; – 1} \right]} h\left( x \right)\end{array}\)
Ta có: \(h’\left( x \right) = 2x + 4 = 0 \Leftrightarrow x = – 2\).
BBT
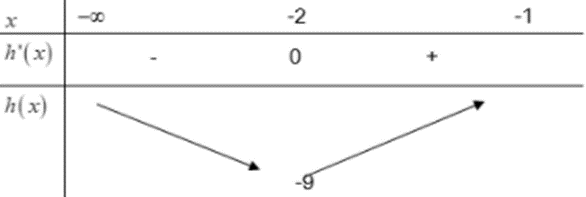
Dựa vào BBT ta có \( – m \le – 9 \Leftrightarrow m \ge 9\).
Mà \(m \in \left[ { – 2019;2019} \right]\) và m nguyên nên \(m \in \left[ {9;10;11;…;2019} \right]\) hay có \(2019 – 9 + 1 = 2011\) giá trị của m thỏa mãn.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left( P \right):2x – 4y + 6z – 1 = 0\). Mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến là:
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \(\left( P \right):2x – 4y + 6z – 1 = 0\). Mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến là:
A. \(\overrightarrow n \left( {1; – 2;3} \right).\)
Đáp án chính xác
B. \(\overrightarrow n \left( {2;4;6} \right).\)
C. \(\overrightarrow n \left( {1;2;3} \right).\)
D. \(\overrightarrow n \left( { – 1;2;3} \right).\)
Trả lời:
Đáp án A
Mặt phẳng \(\left( P \right):2x – 4y + 6z – 1 = 0\) nhận \(\overrightarrow a = \left( {2; – 4;6} \right)\) là một vectơ pháp tuyến.
Xét \(\overrightarrow n = \left( {1; – 2;3} \right)\). Ta có \(\overrightarrow a = 2\overrightarrow n \) nên suy ra \(\overrightarrow a \) và \(\overrightarrow n \) cùng phương. Vậy \(\overrightarrow n = \left( {1; – 2;3} \right)\) cũng là một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương khác 5. Tính \(I = {\log _{\frac{a}{5}}}\left( {\frac{{{a^3}}}{{125}}} \right)\).
Câu hỏi:
Cho a là số thực dương khác 5. Tính \(I = {\log _{\frac{a}{5}}}\left( {\frac{{{a^3}}}{{125}}} \right)\).
A. \(I = – \frac{1}{3}.\)
B. \(I = – 3.\)
C. \(I = \frac{1}{3}.\)
D. \(I = 3.\)
Đáp án chính xác
Trả lời:
Đáp án D
Phương pháp:
Sử dụng công thức: \({\log _a}{b^m} = m{\log _a}b\;\left( {0 < a \ne 1,b > 0} \right)\).
Cách giải:
Ta có \(I = {\log _{\frac{a}{5}}}\left( {\frac{{{a^3}}}{{125}}} \right) = {\log _{\frac{a}{5}}}{\left( {\frac{a}{5}} \right)^3} = 3{\log _{\frac{a}{5}}}\left( {\frac{a}{5}} \right) = 3.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau:
Hàm số nghịch biến trên khoảng nào sau đây?
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau:
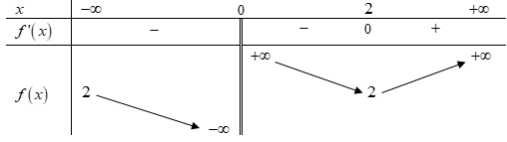
Hàm số nghịch biến trên khoảng nào sau đây?A. \(\left( { – \infty ;2} \right).\)
B. \(\left( {0;2} \right).\)
Đáp án chính xác
C. \(\left( {2; + \infty } \right).\)
D. \(\left( {0; + \infty } \right).\)
Trả lời:
Đáp án B
Dựa vào bảng biến thiên suy ra hàm số nghịch biến trên \(\left( {0;2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Phương trình \({7^{2{x^2} + 5x + 4}} = 49\) có tổng tất cả các nghiệm bằng:
Câu hỏi:
Phương trình \({7^{2{x^2} + 5x + 4}} = 49\) có tổng tất cả các nghiệm bằng:
A. 1.
B. \(\frac{5}{2}.\)
C. \( – 1.\)
D. \( – \frac{5}{2}.\)
Đáp án chính xác
Trả lời:
Đáp án D
Phương pháp:
Đưa về cùng cơ số: \({a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow f\left( x \right) = g\left( x \right)\;\left( {0 < a \ne 1} \right)\).
Cách giải:
Ta có \({7^{2{x^2} + 5x + 4}} = 49 = {7^2} \Leftrightarrow 2{x^2} + 5x + 4 = 2 \Leftrightarrow \left[ \begin{array}{l}x = – \frac{1}{2}\\x = – 2\end{array} \right..\)
Vậy tổng các nghiệm của phương trình là \( – \frac{1}{2} – 2 = – \frac{5}{2}.\)====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 2n + 5\). Số hạng \({u_4}\) bằng:
Câu hỏi:
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = 2n + 5\). Số hạng \({u_4}\) bằng:
A. 19.
B. 11.
C. 21.
D. 13.
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \({u_4} = 2.4 + 5 = 13\).====== **** mời các bạn xem câu tiếp bên dưới **** =====