Cho biểu thức  L = 1- z+ z2- z3+ …+ z2016- z2017  với . Biểu thức  L  có giá trị là

Câu hỏi:

Cho biểu thức  L = 1- z+ z²– z³+ …+ z²⁰¹⁶– z²⁰¹⁷  với 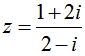. Biểu thức  L  có giá trị là

A. 1 – i.

Đáp án chính xác

B. 1 + i.

Trả lời:

Chọn  A.
+ Ta có: 

+ Khi đó: L = 1- z+ z²– z³+ …+ z²⁰¹⁶– z²⁰¹⁷

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z1; z2 số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?
   
   

   Câu hỏi:
   

   Cho các số phức z thỏa mãn |z – 2 – 4i| = 2. Gọi z_1; z₂ số phức có module lớn nhất và nhỏ nhất. Tổng phần ảo của hai số phức bằng?

   A. 8i

   B. 4

   C. -8

   D. 8

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Ta có 
   
   + Giá trị lớn nhất của |z| là  đạt được tại
   
   
   + Giá trị nhỏ nhất của |z| là , đạt được tại
   
   
   Vậy tổng phần ảo là: 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 – (1 + 3i) z – 2 + 2i = 0  và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức 
   
   

   Câu hỏi:
   

   Gọi z₁, z₂ lần lượt là hai nghiệm của phương trình z² – (1 + 3i) z – 2 + 2i = 0  và thỏa mãn | z₁| > | z₂|. Tìm giá trị của biểu thức 
   

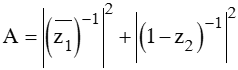
   A. 0,5

   B. 1,5

   Đáp án chính xác

   C. 1

   D. 2

   Trả lời:

   Chọn B.
   Phương trình đã cho tương đương với:
   ( z – 2i) ( z – 1 – i) = 0
   Suy ra: z = 2i hoặc z = 1 + i
   Do | z₁| > | z₂| nên ta có z₁ = 2i và z₂ = 1 + i
   Ta có 
   
   $={\left|\frac{1}{–2i}\right|}^2+{\left|\frac{1}{–i}\right|}^2={\left|\frac{i}{2}\right|}^2+{\left|i\right|}^2=\frac{1}{2}+1=\frac{3}{2}$= 1,5
    

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Gọi z1; z2  lần lượt là hai nghiệm của phương trình z2 – 4z + 7 = 0 .Tính giá trị của biểu thức
   
   

   Câu hỏi:
   

   Gọi z₁; z₂  lần lượt là hai nghiệm của phương trình z² – 4z + 7 = 0 .Tính giá trị của biểu thức

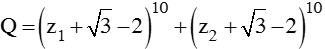
   A. 1

   B. 3

   C. 0

   Đáp án chính xác

   D. 5

   Trả lời:

   Chọn C.
   Phương trình đã cho tương đương với:
   ( z – 2) ² = -3 hay 
   Từ đó 
   Do Q là biểu thức đối xứng với z₁; z₂ nên không mất tính tổng quát, giả sử 
   Lúc đó: 
   
   
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho các số phức z thỏa mãn |z2 + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?
   
   

   Câu hỏi:
   

   Cho các số phức z thỏa mãn |z² + 4| = 2|z|. Kí hiệu M = max|z| và m = min|z|. Tìm module của số phức w = M + m?

   

   Đáp án chính xác

   

   

   

   Trả lời:

   Chọn A.
   Ta có 
   Giải bất phương trình trên với ẩn |z| ta được:
   
   Vậy 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho số phức z1; z2 thỏa mãn . Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z1 – z2 | là?
   
   

   Câu hỏi:
   

   Cho số phức z₁; z₂ thỏa mãn 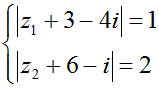. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu thức | z₁ – z₂ | là?

   A. 18

   B. $6\sqrt{2}$

   Đáp án chính xác

   C. 6

   D. $3\sqrt{2}$

   Trả lời:

   Chọn B.
   Ta có
   
   Do đó  và 
   
   Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất là 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====