Câu hỏi:
Cho ba số phức \({z_1},{\rm{ }}{z_2},{\rm{ }}{z_3}\) thỏa mãn \(\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1\); \(\left| {{z_1} – {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\) và \(z_1^2 = {z_2}{z_3}.\) Tính giá trị của \(\left| {{z_2} – {z_3}} \right| – \left| {{z_3} – {z_1}} \right|\).
A. \( – \sqrt 6 – \sqrt 2 – \sqrt 3 .\)
B. \( – \sqrt 6 – \sqrt 2 + \sqrt 3 .\)
C. \(\frac{{\sqrt 6 + \sqrt 2 – 2}}{2}\)
D. \(\frac{{ – \sqrt 6 – \sqrt 2 + 2}}{2}\)
Đáp án chính xác
Trả lời:
Đáp án D
Gọi M, N, P lần lượt là các điểm biểu diễn các số phức \({z_1},{z_2},{z_3}\).
Suy ra M, N, P thuộc đường tròn \(\left( {O;1} \right)\).
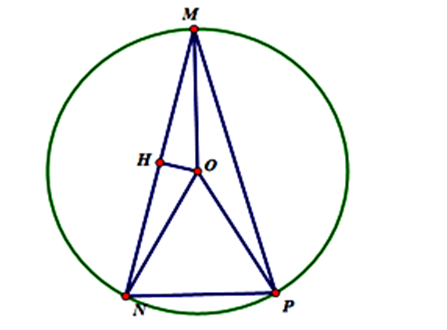
Ta có \(MN = \left| {{z_1} – {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\).
Kẻ \(OH \bot MN \Rightarrow MH = \frac{{MN}}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4} \Rightarrow \cos \widehat {OMN} = \frac{{MN}}{{OM}} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\( \Rightarrow \widehat {OMN} = {15^0} \Rightarrow \widehat {MON} = {150^0}\)
Ta có \(\left| {{z_3} – {z_1}} \right| = \left| {{z_1}} \right|.\left| {{z_3} – {z_1}} \right| = \left| {{z_3}{z_1} – z_1^2} \right| = \left| {{z_3}{z_1} – {z_3}{z_2}} \right| = \left| {{z_3}} \right|.\left| {{z_1} – {z_2}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2}\)
\( \Rightarrow MP = \left| {{z_3} – {z_1}} \right| = \frac{{\sqrt 6 + \sqrt 2 }}{2} \Rightarrow MN = MP = \frac{{\sqrt 6 + \sqrt 2 }}{2}.\)
Tương tự như trên \( \Rightarrow \widehat {MOP} = {150^0} \Rightarrow \widehat {NOP} = {360^0} – \left( {{{150}^0} + {{150}^0}} \right) = {60^0}\)
\( \Rightarrow \Delta NOP\) đều \( \Rightarrow NP = 1\)
\( \Rightarrow \left| {{z_2} – {z_3}} \right| = NP = 1 \Rightarrow \left| {{z_2} – {z_3}} \right| – \left| {{z_3} – {z_1}} \right| = 1 – \frac{{\sqrt 6 + \sqrt 2 }}{2} = \frac{{2 – \sqrt 6 – \sqrt 2 }}{2}.\)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
Câu hỏi:
Cho a là số thực dương tùy ý và \(a \ne 1.\) Mệnh đề nào dưới đây là đúng?
A. \({\log _3}a = {\log _a}3.\)
B. \({\log _3}a = \frac{1}{{{{\log }_3}a}}.\)
C. \({\log _3}a = \frac{1}{{{{\log }_a}3}}.\)
Đáp án chính xác
D. \({\log _3}a = – {\log _a}3.\)
Trả lời:
Đáp án C
Ta có \({\log _3}a = \frac{1}{{{{\log }_a}3}}\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z = – 1 – 2i\)?
Câu hỏi:
Điểm nào trong hình vẽ bên là điểm biểu diễn số phức \(z = – 1 – 2i\)?
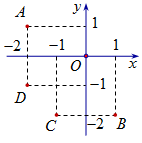
A. Điểm A.
B. Điểm B.
C. Điểm C.
Đáp án chính xác
D. Điểm D.
Trả lời:
Đáp án C
Điểm biểu diễn số phức \(z = – 1 – 2i\) có tọa độ \(\left( { – 1;2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {f\left( x \right)dx} = – 3.\) Tích phân \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
Câu hỏi:
Cho \(\int\limits_0^1 {f\left( x \right)dx} = 2\) và \(\int\limits_1^2 {f\left( x \right)dx} = – 3.\) Tích phân \(\int\limits_0^2 {f\left( x \right)dx} \) bằng
A. 5.
B. \( – 5.\)
C. 1.
D. \( – 1.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(\int\limits_0^2 {f\left( x \right)d{\rm{x}}} = \int\limits_0^1 {f\left( x \right)d{\rm{x}}} + \int\limits_1^2 {f\left( x \right)d{\rm{x}}} = – 1\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian Oxyz, cho hai điểm \(A\left( {2;3;4} \right),{\rm{ }}B\left( {6;2;2} \right).\) Tìm tọa độ của vectơ \(\overrightarrow {AB} .\)
Câu hỏi:
Trong không gian Oxyz, cho hai điểm \(A\left( {2;3;4} \right),{\rm{ }}B\left( {6;2;2} \right).\) Tìm tọa độ của vectơ \(\overrightarrow {AB} .\)
A. \(\overrightarrow {AB} = \left( {4;3;4} \right).\)
B. \(\overrightarrow {AB} = \left( {4; – 1; – 2} \right).\)
Đáp án chính xác
C. \(\overrightarrow {AB} = \left( { – 2;3;4} \right).\)
D. \(\overrightarrow {AB} = \left( {4; – 1;4} \right).\)
Trả lời:
Đáp án B
Ta có \(\overrightarrow {AB} = \left( {4; – 1; – 2} \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
Câu hỏi:
Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình vẽ ?
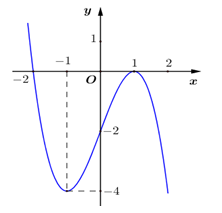
A. \(y = {x^3} – 3{x^2} – 2.\)
B. \(y = {x^3} – 3x – 2.\)
C. \(y = – {x^3} + 3{x^2} – 2.\)
D. \(y = – {x^3} + 3x – 2.\)
Đáp án chính xác
Trả lời:
Đáp án D
Ta có \(y\left( 1 \right) = 0 \Rightarrow \) Loại A và B. Mà \(y\left( { – 1} \right) = – 4\).====== **** mời các bạn xem câu tiếp bên dưới **** =====