Biểu thức sau có modul bằng bao nhiêu 

Câu hỏi:

Biểu thức sau có modul bằng bao nhiêu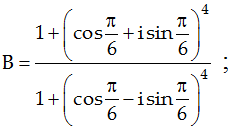 

A. 1

Đáp án chính xác

B. 2

C. 3

D. 4

Trả lời:

Chọn  A.
Ta có:


Số phức trên có modul là 1.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Biết z1; z2 là các số phức thỏa mãn điều kiện . Tìm |z1 + z2|
   
   

   Câu hỏi:
   

   Biết z₁; z₂ là các số phức thỏa mãn điều kiện 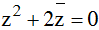. Tìm |z₁ + z₂|

   

   

   

   D. |z₁ + z₂| = 2

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Gọi z = x + yi thì $\overline{z}=x–yi$
   Phương trình đã cho trở thành:
   x² – y² + 2xyi + 2( x – yi) = 0
   Suy ra: x² – y² + 2x + ( 2xy – 2y)i = 0
   
   Với y = 0  thay vào phương trình (*) ta được: x² + 2x = 0 
   Với x = 1 thay vào phương trình (*) ta được:  y² = 3 
   Vậy  Suy ra: |z₁ + z₂| = 2.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Biết z1; z2  là số phức thỏa điều kiện z2 – |z|2 + 1 = 0. Tính 
   
   

   Câu hỏi:
   

   Biết z₁; z₂  là số phức thỏa điều kiện z² – |z|² + 1 = 0. Tính 

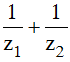
   A. –i

   B. i

   C. 1 + i

   D. 0

   Đáp án chính xác

   Trả lời:

   Chọn D.
   Đặt z = x + yi.  Phương trình z² – |z|² + 1 = 0 trở thành:
   x² – y² + 2xyi – ( x² + y²) + 1 = 0
   Suy ra: -2y² + 1+ 2xyi = 0
   
   Vậy số phức z cần tìm là:  .Suy ra 

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Biết z1; z2; z3; z4  là các số phức thỏa điều kiện . Tính | z1| + | z2| + | z3| + | z4|
   
   

   Câu hỏi:
   

   Biết z₁; z₂; z₃; z₄  là các số phức thỏa điều kiện .
   Tính | z₁| + | z₂| + | z₃| + | z₄|

   A. 3

   Đáp án chính xác

   B. 2

   

   

   Trả lời:

   Chọn A.
   Đặt z = x + yi . Phương trình  trở thành
   ( x – yi)² = i(x + yi)  hay x² – y² – 2xyi = -y + xi
   
   
   Vậy số phức z cần tìm là: z = 0 ; z = i;   
   Suy ra | z₁| + | z₂| + | z₃| + | z₄| = 3.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho số phức z thỏa điều kiện . Tìm khẳng định đúng
   
   

   Câu hỏi:
   

   Cho số phức z thỏa điều kiện 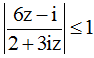. Tìm khẳng định đúng

   A. |z| ≥ 1

   B. |z|  ≤ 3

   C. |z| ≤ 1/3

   Đáp án chính xác

   D. |z| > 1/3

   Trả lời:

   Chọn  C.
   Ta có: 
   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Gọi z là số phức khác 0 sao cho  .Tìm khẳng định đúng
   
   

   Câu hỏi:
   

   Gọi z là số phức khác 0 sao cho 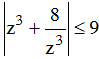 .Tìm khẳng định đúng

   

   Đáp án chính xác

   

   

   

   Trả lời:

   Chọn  A.
   Ta có:
   , mặt khác ta có:
   |z₁ + z₂| ≤ |z₁| + |z₂|.
   Do đó:
   
   Đặt  lúc đó ta được: a³ – 6a – 9 ≤ 0 hay ( a – 3) ( a² + 3a + 3) ≤ 0
   Suy ra: a ≤ 3.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====