Cho đồ thị hàm số y=fx   xác định trên khoảng a;b  như hình vẽ. Dựa vào hình vẽ hãy cho biết tại mỗi điểm   x1,x2,x3,x4. a, Hàm số có liên tục không? b, Hàm số có đạo hàm không?  

Câu hỏi:

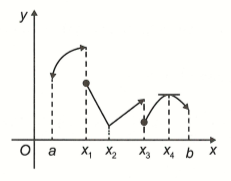
Cho đồ thị hàm số $y=f\left(x\right)$   xác định trên khoảng $\left(a;b\right)$  như hình vẽ.
Dựa vào hình vẽ hãy cho biết tại mỗi điểm   $x_1,x_2,x_3,x_4.$
a, Hàm số có liên tục không?
b, Hàm số có đạo hàm không?

 

Trả lời:

 
a, Hàm số gián đoạn tại các điểm $x_1,x_3$  vì đồ thị bị đứt tại các điểm đó. Hàm số liên tục tại $x_2,x_4$  vì đồ thị là đường liền nét khi đi qua các điểm đó.
b, Tại các điểm $x_1,x_3$  hàm số không có đạo hàm do hàm số gián đoạn tại các điểm $x_1,x_3.$
Hàm số không có đạo hàm tại $x_2$  vì đồ thị bị gãy (không có tiếp tuyến tại đó).
Hàm số có đạo hàm tại $x_4$  và  vì tại$f^{‘}\left(x_4\right)=0$  đồ thị hàm số có tiếp tuyến và tiếp tuyến song song với trục hoành (hệ số góc của tiếp tuyến bằng 0).

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Dùng định nghĩa tính đạo hàm của hàm số y=2×2+3  tại x0=2 .
   
   

   Câu hỏi:
   

   Dùng định nghĩa tính đạo hàm của hàm số $y=2x^2+3$  tại $x_0=2$ .

   Trả lời:

   Giả sử  là số gia của đối số tại .
   Ta có: $\Delta y=f\left(2+\Delta x\right)-f\left(2\right)=2{\left(2+\Delta x\right)}^2+3-\left({2.2}^2+3\right)$

   $=2\Delta x\left(\Delta x+4\right).$                 
   Tỉ số $\frac{\Delta y}{\Delta x}=\frac{2\Delta x\left(\Delta x+4\right)}{\Delta x}=2\Delta x+8$ .
   $\lim \Delta x\to 0\frac{\Delta y}{\Delta x}=\lim \Delta x\to 0\left(2\Delta x+8\right)=8.$

   Vậy $f^{‘}\left(2\right)=8.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Dùng định nghĩa tính đạo hàm của hàm số y=2x−1x+1  tại x0=3 .
   
   

   Câu hỏi:
   

   Dùng định nghĩa tính đạo hàm của hàm số $y=\frac{2x-1}{x+1}$  tại $x_0=3$ .

   Trả lời:

   Giả sử $\Delta x$  là số gia của đối số tại $x_0=3$ .
   Ta có: $\Delta y=f\left(3+\Delta x\right)-f\left(3\right)=\frac{2\left(3+\Delta x\right)-1}{3+\Delta x+1}-\frac{5}{4}=\frac{5+2\Delta x}{4+\Delta x}-\frac{5}{4}=\frac{3\Delta x}{4\left(4+\Delta x\right)};$
            $\frac{\Delta y}{\Delta x}=\frac{3\Delta x}{\Delta x.4\left(4+\Delta x\right)}=\frac{3}{4\left(4+\Delta x\right)}.$  
   Do đó $\lim \Delta x\to 0\frac{\Delta y}{\Delta x}=\lim \Delta x\to 0\frac{3\Delta x}{\Delta x.4\left(4+\Delta x\right)}=\lim \Delta x\to 0\frac{3}{4\left(4+\Delta x\right)}=\frac{3}{16}.$
   Vậy $f^{‘}\left(3\right)=\frac{3}{16}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Dùng định nghĩa tính đạo hàm của hàm số y=2x−1tại x0=1.
   
   

   Câu hỏi:
   

   Dùng định nghĩa tính đạo hàm của hàm số $y=\sqrt{2x-1}$tại $x_0=1.$

   Trả lời:

   Giả sử $\Delta x$  là số gia của đối số tại $x_0=1.$
   Ta có: $\Delta y=f\left(1+\Delta x\right)-f\left(1\right)=\sqrt{2\left(1+\Delta x\right)-1}-1=\frac{2\Delta x}{\sqrt{2\Delta x+1}+1};$
       $\frac{\Delta y}{\Delta x}=\frac{2\Delta x}{\Delta x\left(\sqrt{2\Delta x+1}+1\right)}=\frac{2}{\sqrt{2\Delta x+1}+1};$       
        $\lim \Delta x\to 0\frac{\Delta y}{\Delta x}=\lim \Delta x\to 0\frac{2}{\sqrt{2\Delta x+1}+1}=1$       .
   Vậy $f^{‘}\left(1\right)=1.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Dùng định nghĩa tính đạo hàm của hàm số y=sinx  tại x0=π3.
   
   

   Câu hỏi:
   

   Dùng định nghĩa tính đạo hàm của hàm số $y=\sin x$  tại $x_0=\frac{\pi }{3}.$

   Trả lời:

   Giả sử $\Delta x$  là số gia của đối số $x_0=\frac{\pi }{3}.$
   Ta có: $\Delta y=f\left(\frac{\pi }{3}+\Delta x\right)-f\left(\frac{\pi }{3}\right)=\sin \left(\frac{\pi }{3}+\Delta x\right)-\sin \frac{\pi }{3}=2\cos \left(\frac{\pi }{3}+\frac{\Delta x}{2}\right)\sin \frac{\Delta x}{2};$
           $\frac{\Delta y}{\Delta x}=\cos \left(\frac{\pi }{3}+\frac{\Delta x}{2}\right)\frac{\sin \frac{\Delta x}{2}}{\frac{\Delta x}{2}}.$   
   Do đó $\lim \Delta x\to 0\frac{\Delta y}{\Delta x}=\lim \Delta x\to 0\cos \left(\frac{\pi }{3}+\frac{\Delta x}{2}\right)\frac{\sin \frac{\Delta x}{2}}{\frac{\Delta x}{2}}.$
   Vì $\lim \Delta x\to 0\frac{\sin \frac{\Delta x}{2}}{\frac{\Delta x}{2}}=1$  nên $\lim \Delta x\to 0\frac{\Delta y}{\Delta x}=\lim \Delta x\to 0\cos \left(\frac{\pi }{3}+\frac{\Delta x}{2}\right)=\cos \frac{\pi }{3}=\frac{1}{2}$ .
   Vậy $f^{‘}\left(\frac{\pi }{3}\right)=\frac{1}{2}.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Chứng minh rằng hàm số fx=x−12,x≥0−x2,x
   
   

   Câu hỏi:
   

   Chứng minh rằng hàm số $f\left(x\right)=\left\{\begin{array}{l}{\left(x-1\right)}^2,x\ge 0\\ -x^2,x<0\end{array}\right.$   không có đạo hàm tại  nhưng có đạo
   hàm tại $x=2$  .

   Trả lời:

   Ta có $\lim x\to 0^{+}f\left(x\right)=\lim x\to 0^{+}{\left(x-1\right)}^2=1;\lim x\to 0^{-}f\left(x\right)=\lim x\to 0^{-}\left(-x^2\right)=0\Rightarrow \lim x\to 0^{+}f\left(x\right)\ne \lim x\to 0^{-}f\left(x\right).$

   Suy ra hàm số gián đoạn tại   nên không có đạo hàm tại đó.
   $\lim \Delta x\to 0\frac{f\left(2+\Delta x\right)-f\left(2\right)}{\Delta x}=\lim \Delta x\to 0\frac{{\left(1+\Delta x\right)}^2-1^2}{\Delta x}=\lim \Delta x\to 0\left(2+\Delta x\right)=2.$

   Vậy hàm số $y=f\left(x\right)$  có đạo hàm tại $x=2$  và $f^{‘}\left(2\right)=2.$

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====