Tứ giác ABCD là hình gì nếu AB→ = DC→ và AB→=DC→

Câu hỏi:

Tứ giác ABCD là hình gì nếu $\overrightarrow{AB} = \overrightarrow{DC} và \left|\overrightarrow{AB}\right|=\left|\overrightarrow{DC}\right|$

Trả lời:

 tứ giác ABCD là hình bình hành⇒ tứ giác ABCD là hình thoi.(Hình bình hành có hai cạnh kề bằng nhau là hình thoi)

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Cho lục giác đều ABCDEF tâm O. Hãy chỉ ra các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác.
   
   

   Câu hỏi:
   

   Cho lục giác đều ABCDEF tâm O. Hãy chỉ ra các vectơ bằng vectơ AB có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác.

   Trả lời:

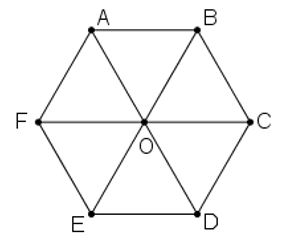   Các vecto bằng vecto $\overrightarrow{AB}$ là: $\overrightarrow{FO},\overrightarrow{ OC},\overrightarrow{ ED}$.Vậy các vecto có điểm đầu và điểm cuối là O hoặc các đỉnh của lục giác đều và bằng $\overrightarrow{AB}$ là: $\overrightarrow{FO},\overrightarrow{ OC},\overrightarrow{ ED}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?a, Hai vecto cùng hướng thì cùng phương.b, Hai vecto b→ và kb→ cùng phương.c, Hai vecto a→ và (-2)a→ cùng hướng.d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.
   
   

   Câu hỏi:
   

   Cho hai vectơ a và b đều khác vectơ 0. Các khẳng định sau đúng hay sai?a, Hai vecto cùng hướng thì cùng phương.b, Hai vecto b→ và kb→ cùng phương.c, Hai vecto a→ và (-2)a→ cùng hướng.d) Hai vector ngược hướng với vector thứ ba khác vectơ 0→ thì cùng phương.

   Trả lời:

   a) Đúngb) Đúngc) Said) Đúng

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC nội tiếp đường tròn tâm O. Hãy xác định các điểm M, N, P sao cho:

   Trả lời:

   a)  M là đỉnh còn lại của hình bình hành AOBM.+ AOBM là hình bình hành ⇒ AM = OBMà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)+ AOBM là hình bình hành ⇒ AM//BOTừ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.Mà  nên M là điểm chính giữa cung b) Chứng minh tương tự phần a) ta có:  N là điểm chính giữa cung BC.c)  P là điểm chính giữa cung CA.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho tam giác đều ABC có cạnh bằng a. Tính:
   
   

   Câu hỏi:
   

   Cho tam giác đều ABC có cạnh bằng a. Tính:

   Trả lời:

   Vẽ hình bình hành ABDC, gọi H là giao điểm của AD và BC.+ Hình bình hành ABDC có AB = AC ⇒ ABDC là hình thoi ⇒ AD ⊥ BC tại H.+ H là trung điểm BC ⇒ BH = BC/2 = a/2.+ ΔABH vuông tại H nên:+ H là trung điểm AD ⇒ AD = 2. AH = a√3.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho sáu điểm M, N, P, Q, R, S bất kỳ. Chứng minh rằng:
   
   

   Câu hỏi:
   

   Cho sáu điểm M, N, P, Q, R, S bất kỳ. Chứng minh rằng:

   Trả lời:

   Áp dụng quy tắc ba điểm ta có:

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====