Tính diện tích bề mặt của một miếng bánh mì kebab hình tam giác có hai cạnh lần lượt là 10cm và 12cm và góc được tạo bởi hai cạnh đó là 35°.

Câu hỏi:

Tính diện tích bề mặt của một miếng bánh mì kebab hình tam giác có hai cạnh lần lượt là 10cm và 12cm và góc được tạo bởi hai cạnh đó là 35°.

Trả lời:

Lời giải
Diện tích bề mặt miếng bánh mì kebab là:
S = \(\frac{1}{2}\).10.12.sin35° ≈ 34,4 (cm²).
Vậy diện tích bề mặt miếng bánh mì kebab khoảng 34,4 cm².

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Tính độ dài các cạnh chưa biết trong tam giác sau:
   
   

   Câu hỏi:
   

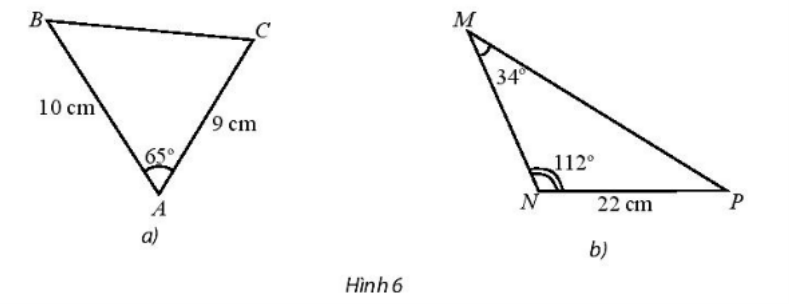
   Tính độ dài các cạnh chưa biết trong tam giác sau:
   

   Trả lời:

   Lời giải
   a) Áp dụng định lí côsin ta có:
   BC² = AB² + AC² – 2.AB.AC.cos\(\widehat {\rm{A}}\)
   BC² = 10² + 9² – 2.10.9.cos65°
   BC ² ≈ 104,929
   BC ≈ 10,24 (cm).
   Vậy BC ≈ 10,24 (cm).
   b) \(\widehat {\rm{P}}\)= 180° – 112° – 34° = 34°.
   Ta có: \(\widehat {\rm{P}}\) = \(\widehat {\rm{M}}\) ⇒ tam giác MNP cân tại N ⇒ MN = NP = 22 (cm)
   Áp dụng định lí sin ta có: \(\frac{{{\rm{MP}}}}{{{\rm{sinN}}}}{\rm{ = }}\frac{{{\rm{MN}}}}{{{\rm{sinP}}}}{\rm{ = }}\frac{{{\rm{NP}}}}{{{\rm{sinM}}}} = \frac{{22}}{{\sin 34^\circ }}\).
   ⇒ MP = \(\frac{{22}}{{\sin 34^\circ }}\).sin112° ≈ 36,48 (cm)
   Vậy MP ≈ 36,48 cm, MN = 22 cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Cho tam giác ABC biết cạnh a = 75 cm, \(\widehat {\rm{B}}\) = 80°, \(\widehat {\rm{C}}\)= 40°. Tính các góc, các cạnh còn lại của tam giác ABC.
   
   

   Câu hỏi:
   

   Cho tam giác ABC biết cạnh a = 75 cm, \(\widehat {\rm{B}}\) = 80°, \(\widehat {\rm{C}}\)= 40°.
   Tính các góc, các cạnh còn lại của tam giác ABC.

   Trả lời:

   Lời giải
   Ta có: \(\widehat {\rm{A}}\)= 180° – 80° – 40° = 60°.
   Áp dụng định lí sin ta có:
   \(\frac{{\rm{a}}}{{{\rm{sinA}}}}{\rm{ = }}\frac{{\rm{b}}}{{{\rm{sinB}}}}{\rm{ = }}\frac{{\rm{c}}}{{{\rm{sinC}}}}\) = \(\frac{{75}}{{\sin 60^\circ }}\)
   ⇒ b = \(\frac{{75}}{{\sin 60^\circ }}\). sin80° ≈ 85,29 (cm);
   ⇒ c = \(\frac{{75}}{{\sin 60^\circ }}\). sin40° ≈ 55,67 (cm).
   Vậy AC ≈ 85,29 cm; AB ≈ 55,67 cm và \(\widehat {\rm{A}}\)= 60°.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tính bán kính đường tròn ngoại tiếp tam giác ABC.
   
   

   Câu hỏi:
   

   Tính bán kính đường tròn ngoại tiếp tam giác ABC.

   Trả lời:

   Lời giải

   R = \(\frac{{\rm{a}}}{{{\rm{2sinA}}}}\) = \(\frac{{75}}{{2.\sin 60^\circ }}\) = 25\(\sqrt 3 \) (cm).
   Vậy R = 25\(\sqrt 3 \) cm.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm góc lớn nhất của tam giác ABC, biết a = 8, b = 12, c = 6.
   
   

   Câu hỏi:
   

   Tìm góc lớn nhất của tam giác ABC, biết a = 8, b = 12, c = 6.

   Trả lời:

   Lời giải
   Do b là cạnh lớn nhất nên B là góc lớn nhất.
   Theo định lí côsin: b² = a² + c² – 2accosB
   ⇒ cosB = \(\frac{{{{\rm{a}}^2} + {{\rm{c}}^2} – {{\rm{b}}^2}}}{{2{\rm{ac}}}}\) = \(\frac{{{8^2} + {6^2} – {{12}^2}}}{{2.8.6}}\)
   ⇒ cosB = \(\frac{{ – 11}}{{24}}\).
   ⇒ \(\widehat {\rm{B}}\) = 117°16’46’’.
   Vậy góc lớn nhất của tam giác ABC là \(\widehat {\rm{B}}\) = 117°16’46’’.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Tính khoảng cách giữa hai điểm P và Q của một hồ nước ( Hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400m và 600m người quan sát nhìn thấy một góc 76°.
   
   

   Câu hỏi:
   

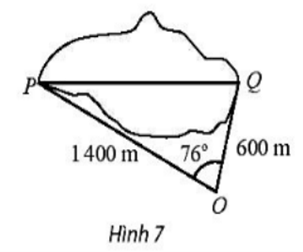
   Tính khoảng cách giữa hai điểm P và Q của một hồ nước ( Hình 7). Cho biết từ một điểm O cách hai điểm P và Q lần lượt là 1400m và 600m người quan sát nhìn thấy một góc 76°.
   

   Trả lời:

   Lời giải
   Áp dụng định lí côsin:
   PQ² = OP² + OQ² – 2.OP.OQ.cos\(\widehat {\rm{O}}\)
   PQ² = 1400² + 600² – 2.1400.600.cos76°
   PQ = \(\sqrt {{{1400}^2} + {{600}^2}–{\rm{ }}2.1400.600.{\rm{cos}}76^\circ } \)
   PQ ≈ 1383,32 (m).
   Vậy khoảng cách giữa hai điểm PQ là PQ ≈ 1383,32 (m).

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====