Hệ phương trình x2=3x−yy2=3y−xcó bao nhiêu nghiệm?

Câu hỏi:

Hệ phương trình $\left\{\begin{array}{c}{x}^2=3x-y\\ y^2=3y-x\end{array}\right.$có bao nhiêu nghiệm?

A. 3

B. 2

Đáp án chính xác

C. 1

D. 4

Trả lời:

$\left\{\begin{array}{c}{x}^2=3x-y\left(1\right)\\ y^2=3y-x\left(2\right)\end{array}\right.$Lấy (1) trừ (2) theo vế ta được:$x^2-y^2=4x-4y\iff \left(x-y\right)\left(x+y-4\right)=0\iff \left[\begin{array}{c}y=x\\ y=4-x\end{array}\right.$TH1: $\left\{\begin{array}{c}{x}^2=3x-y\\ y=x\end{array}\right.\iff \left\{\begin{array}{c}{x}^2-2x=0\\ y=x\end{array}\iff \left[\begin{array}{c}x=y=0\\ x=y=2\end{array}\right.\right.$TH2: $\left\{\begin{array}{c}{x}^2=3x-y\\ y=4-x\end{array}\iff \left\{\begin{array}{c}{x}^2-4x+4=0\\ y=4-x\end{array}\right.\right.\iff x=y=2$Vậy hệ có hai nghiệmĐáp án cần chọn là: B

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Hỏi có bao nhiêu giá trị m nguyên trong đoạn [0; 2017] để phương trình x2-4x-5-m=0 có hai nghiệm phân biệt?
   
   

   Câu hỏi:
   

   Hỏi có bao nhiêu giá trị m nguyên trong đoạn [0; 2017] để phương trình $\left|x^2–4\left|x\right|–5\right|–m=0$ có hai nghiệm phân biệt?

   A. 2016

   B. 2008

   C. 2009

   Đáp án chính xác

   D. 2017

   Trả lời:

   PT: $\left|x^2–4\left|x\right|–5\right|–m=0\iff \left|x^2–4\left|x\right|–5\right|=m\left(1\right)$Số nghiệm phương trình (1) bằng số giao điểm của đồ thị hàm số $y=\left|x^2–4\left|x\right|–5\right|\left(P\right)$ và đường thẳng $y=m$ (cùng phương Ox)Xét hàm số $y=x^2–4x–5\left(P_1\right)$ có đồ thị như hình 1. Xét hàm số $y=x^2–4\left|x\right|–5\left(P_2\right)$ là hàm số chẵn nên có đồ thị nhận Oy làm trục đối xứng.Mà $y=x^2–4\left|x\right|–5=x^2–4x–5$ nếu $x\ge 0$Suy ra đồ thị hàm số $\left(P_2\right)$ gồm hai phần:Phần 1: Giữ nguyên đồ thị hàm số $\left(P_1\right)$ phần bên phải Oy.Phần 2: Lấy đối xứng phần 1 qua trục Oy.Ta được đồ thị $\left(P_2\right)$ như hình 2.Xét hàm số $y=\left|x^2–4\left|x\right|–5\right|\left(P\right)$, ta có: $\left\{\begin{array}{c}{x}^2-4\left|x\right|-5(y\ge 0)\\ -\left(x^2-4\left|x\right|-5\right)(y<0)\end{array}\right.$Suy ra đồ thị hàm số (P) gồm hai phần:Phần 1: Giữ nguyên đồ thị hàm số $\left(P_2\right)$ phần trên Ox.Phần 2: Lấy đối xứng đồ thị hàm số $\left(P_2\right)$ phần dưới Ox qua trục Ox.Ta được đồ thị (P) như hình 3.Quan sát đồ thị hàm số (P) ta có:Phương trình |x² – 4 |x| − 5| − m = 0 (1) có hai nghiệm phân biệt $\iff \left\{\begin{array}{c}m>9\\ m=0\end{array}\right.$Mà $\left\{\begin{array}{c}m\in Z\\ m\in \left[0;2017\right]\end{array}\right.\Rightarrow m\in \left\{0;10;11;12;...;2017\right\}$Vậy có 2009 giá trị nguyên của m thỏa mãn.Đáp án cần chọn là: C

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Tìm m để phương trình x2-mx+m2-3=0 có hai nghiệm x1, x2 là độ dài các cạnh góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng 2 là
   
   

   Câu hỏi:
   

   Tìm m để phương trình $x^2–mx+m^2–3=0$ có hai nghiệm $x_1, x_2$ là độ dài các cạnh góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng 2 là

   A. $m\in \left(0;2\right)$
    

   B. $m=\pm \sqrt{2}$

   C. $m\in \left(–2;0\right)$

   D. $m\in \varnothing$

   Đáp án chính xác

   Trả lời:

   Phương trình $x^2–mx+m^2–3=0$ có hai nghiệm $x_1, x_2$ là độ dài các cạnh góc vuông của một tam giác vuông với cạnh huyền có độ dài bằng 2 khi và chỉ khi: $\left\{\begin{array}{c}\Delta =m^2-4m^2+12\ge 0\\ S=x_1+x_2=m>0\\ P=x_1.x_2>0\\ x_1^2+x_2^2=4\end{array}\right.\iff \left\{\begin{array}{c}3<m\le 4\\ m>0\\ {\left(x_1+x_2\right)}^2-2x_1{x}_2=4\end{array}\right.$$\iff \left\{\begin{array}{c}\sqrt{3}<m\le 2\\ m^2-2\left(m^2-3\right)=4\end{array}\right.\iff \left\{\begin{array}{c}\sqrt{3}<m\le 2\\ m^2=2\end{array}\right.\iff m\in \varnothing$Đáp án cần chọn là: D

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Tất cả các giá trị của tham số m để phương trình x2+1×2−2mx+1x+1=0 có nghiệm là:
   
   

   Câu hỏi:
   

   Tất cả các giá trị của tham số m để phương trình $\left(x^2+\frac{1}{x^2}\right)-2m\left(x+\frac{1}{x}\right)+1=0$ có nghiệm là:

   A. $m\in \left[\frac{3}{4};+\infty \right)$
    

   B. $m\in \left(-\infty ;\frac{3}{4}\right]\cup \left[\frac{3}{4};+\infty \right)$

   Đáp án chính xác

   C. $m\in \left(-\infty ;-\frac{3}{4}\right]$

   D. $m\in \left(-\frac{3}{4};\frac{3}{4}\right)$

   Trả lời:

   Ta có: $\left(x^2+\frac{1}{x^2}\right)-2m\left(x+\frac{1}{x}\right)+1=0$${\left(x+\frac{1}{x}\right)}^2-2m\left(x+\frac{1}{x}\right)-1=0\left(1\right)$ Đặt $x+\frac{1}{x}=t,\left|t\right|\ge 2$ ta được $t^2-2mt-1=0\left(2\right)$Phương trình (2) luôn có hai nghiệm $t_1<0<t_2$ $\left(do a,c=–1<0a\right)$ ⇒ phương trình (1) có nghiệm khi và chỉ khi phương trình (2) có ít nhất một nghiệm t sao cho $\left|t\right|\ge 2$, hay ít nhất một trong hai số 2; −2 phải nằm giữa hai nghiệm 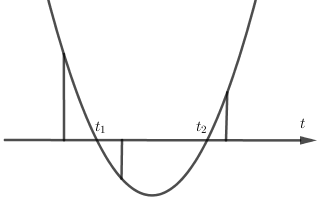$t_1,t_2$ hay $\left[\begin{array}{c}f\left(2\right)\le 0\\ f(-2)\le 0\end{array}\right.$$\iff \left[\begin{array}{c}3-4m\le 0\\ 3+4m\le 0\end{array}\right.\iff \left[\begin{array}{c}m\ge \frac{3}{4}\\ m\le -\frac{3}{4}\end{array}\right.$ Đáp án cần chọn là: B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Tìm tất cả các giá trị thực của m để phương trình x2−4x+6+3m=0 có nghiệm thuộc đoạn −1;3:
   
   

   Câu hỏi:
   

   Tìm tất cả các giá trị thực của m để phương trình $x^2-4x+6+3m=0$ có nghiệm thuộc đoạn $\left[-1;3\right]$:

   A. $\frac{2}{3}\le m\le \frac{11}{3}$
    

   B. $-\frac{11}{3}\le m\le -\frac{2}{3}$

   Đáp án chính xác

   C. $-1\le m\le -\frac{2}{3}$

   D. $-\frac{11}{3}\le m\le -1$

   Trả lời:

   Ta có: $x^2–4x+6+3m=0\iff 3m=–x^2+4x–6$Số nghiệm của phương trình $x^2–4x+6+3m=0$ là số giao điểm của đường thẳng $y=3m$ và parabol $y=–x^2+4x–6$Parabol $y=–x^2+4x–6$ có hoành độ đỉnh $x=2\in \left[–1;3\right]$, hệ số $a=–1<0$ nên đồng biến khi $x<2$ và nghịch biến khi $x>2$.Bảng biến thiên của hàm số $y=–x^2+4x–6$ tr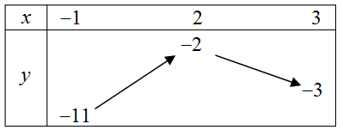ên đoạn $\left[–1;3\right]$: Từ bảng biến thiên ta thấy, nếu phương trình có nghiệm trên đoạn $\left[–1;3\right]$ thì đường thẳng $y=3m$ phải cắt parabol tại ít nhất 1 điểm có hoành độ thuộc đoạn $\left[–1;3\right]$.Phương trình có nghiệm thuộc đoạn $\left[–1;3\right]$$\iff –11\le 3m\le –2$$\iff -\frac{11}{3}\le m\le -\frac{2}{3}$Đáp án cần chọn là: B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Xác định m để phương trình m=x2-6x-7 có 4 nghiệm phân biệt.
   
   

   Câu hỏi:
   

   Xác định m để phương trình $m=\left|x^2–6x–7\right|$ có 4 nghiệm phân biệt.

   A. m ∈ (−16; 16).

   B. m ∈ (0; 16)

   Đáp án chính xác

   C. m ∈ ∅.

   D. m ∈ [0; 16].

   Trả lời:

   $m=\left|x^2–6x–7\right|$ là phương trình hoành độ giao điểm của đường thẳng y = m và đồ thị (C): $y=\left|x^2–6x–7\right|$Vẽ (P): $y=x^2–6x–7$, lấy đối xứng phần phía dưới Ox của (P) lên trên Ox và xóa đi phần phía dưới Ox (vì $y=\left|x^2–6x–7\right|$,$\forall x\in R$), ta được đồ thị (C).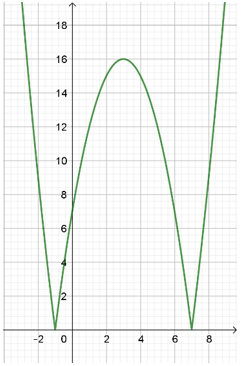Dựa vào đồ thị: phương trình $m=\left|x^2–6x–7\right|$ có 4 nghiệm phân biệt khi $m\in \left(0;16\right)$.Đáp án cần chọn là: B

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====