SBT Toán 9 Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai | Giải SBT Toán lớp 9

Giải SBT Toán 9 Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai

Bài 68 trang 16 SBT Toán 9 tập 1: Khử mẫu của mỗi biểu thức lấy căn và rút gọn ( nếu được): 

a) $\sqrt{\frac{2}{3}}$;

b) $\sqrt{{\frac{x}{5}}^2}$ với  $x\ge 0$;

c) $\sqrt{\frac{3}{x}}$ với $x>0$;

d) $\sqrt{x^2-{\frac{x}{7}}^2}$ với $x<0$.

Phương pháp giải:

Với $A,B$ mà $A.B\ge 0$ và $B\ne 0$ ta có:

$\sqrt{\frac{A}{B}}=\sqrt{\frac{AB}{B^2}}=\frac{\sqrt{AB}}{\left|B\right|}.$

Lời giải:

a)

$\sqrt{\frac{2}{3}}$ =  $\sqrt{\frac{2.3}{3^2}}=\frac{1}{3}\sqrt{6}$

 b)

$\sqrt{{\frac{x}{5}}^2}$ $=\sqrt{\frac{x^2}{5}}=\sqrt{\frac{x^2.5}{5^2}}=\frac{x}{5}\sqrt{5}$ (với $x\ge 0$)

 c)

$\sqrt{\frac{3}{x}}$ $=\sqrt{\frac{3x}{x^2}}=\frac{1}{\left|x\right|}\sqrt{3x}=\frac{1}{x}\sqrt{3x}$ (với $x>0$)

 d)

$\sqrt{x^2-{\frac{x}{7}}^2}$ $=\sqrt{\frac{7x^2-x^2}{7}}$

$=\sqrt{\frac{6x^2}{7}}$$=\sqrt{\frac{42x^2}{49}}$$=\frac{\left|x\right|}{7}\sqrt{42}=-\frac{x}{7}\sqrt{42}$ (với $x<0$)  

Bài 69 trang 16 SBT Toán 9 tập 1: Trục căn thức ở mẫu và rút gọn (nếu được): 

a) $\frac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}$;

b) $\frac{26}{5-2\sqrt{3}}$;

c) $\frac{2\sqrt{10}-5}{4-\sqrt{10}}$;

d) $\frac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}$. 

Phương pháp giải:

Áp dụng: 

$\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}$ với $B>0$. 

Lời giải:

a)

$\frac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}$ $=\frac{(\sqrt{5}-\sqrt{3})\sqrt{2}}{{(\sqrt{2})}^2}=\frac{\sqrt{10}-\sqrt{6}}{2}$ 

 b)

$\frac{26}{5-2\sqrt{3}}$ $=\frac{26(5+2\sqrt{3})}{(5-2\sqrt{3})(5+2\sqrt{3})}$ $=\frac{26(5+2\sqrt{3})}{25-12}$

$=\frac{26(5+2\sqrt{3})}{13}$ $=2(5+2\sqrt{3})=10+4\sqrt{3}$  

 c)

$\frac{2\sqrt{10}-5}{4-\sqrt{10}}$ $=\frac{2\sqrt{2.5}-\sqrt{5^2}}{2\sqrt{2^2}-\sqrt{2.5}}$

$=\frac{\sqrt{5}(2\sqrt{2}-\sqrt{5})}{\sqrt{2}(2\sqrt{2}-\sqrt{5})}=\frac{\sqrt{5}}{\sqrt{2}}=\frac{\sqrt{5}.\sqrt{2}}{{(\sqrt{2})}^2}$ $=\frac{\sqrt{10}}{2}$

 d)

$\frac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}$ $=\frac{3(\sqrt{3}{)}^2-2\sqrt{3}}{3\sqrt{3.2}-2\sqrt{2}}$

$=\frac{\sqrt{3}(3\sqrt{3}-2)}{\sqrt{2}(3\sqrt{3}-2)}=\frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{3.}\sqrt{2}}{{(\sqrt{2})}^2}$ $=\frac{\sqrt{6}}{2}$ 

Bài 70 trang 16 SBT Toán 9 tập 1: Rút gọn các biểu thức: 

a) $\frac{2}{\sqrt{3}-1}-\frac{2}{\sqrt{3}+1}$

b) $\frac{5}{12(2\sqrt{5}+3\sqrt{2})}$$-\frac{5}{12(2\sqrt{5}-3\sqrt{2})}$

c) $\frac{5+\sqrt{5}}{5-\sqrt{5}}+\frac{5-\sqrt{5}}{5+\sqrt{5}}$

d) $\frac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\frac{\sqrt{3}}{\sqrt{\sqrt{3}+1}+1}$ 

Phương pháp giải:

Quy đồng mẫu các phân thức.

Sử dụng hằng đẳng thức: $a^2-b^2=(a+b)(a-b)$ 

Sử dụng: $\sqrt{A}.\sqrt{B}=\sqrt{A.B}$ với $A\ge 0,B\ge 0$.

Lời giải:

a)

$\frac{2}{\sqrt{3}-1}-\frac{2}{\sqrt{3}+1}$ $=\frac{2(\sqrt{3}+1)-2(\sqrt{3}-1)}{(\sqrt{3}+1)(\sqrt{3}-1)}$

$=\frac{2\sqrt{3}+2-2\sqrt{3}+2}{3-1}=\frac{4}{2}=2$

 b)

$\frac{5}{12(2\sqrt{5}+3\sqrt{2})}-\frac{5}{12(2\sqrt{5}-3\sqrt{2})}$

$=\frac{5(2\sqrt{5}-3\sqrt{2})-5(2\sqrt{5}+3\sqrt{2})}{12(2\sqrt{5}+3\sqrt{2})(2\sqrt{5}-3\sqrt{2})}$ 

$\begin{array}{rl}& =\frac{10\sqrt{5}-15\sqrt{2}-10\sqrt{5}-15\sqrt{2}}{12(20-18)}\\ & =\frac{-30\sqrt{2}}{12.2}=-\frac{5\sqrt{2}}{4}\end{array}$

c)

$\frac{5+\sqrt{5}}{5-\sqrt{5}}+\frac{5-\sqrt{5}}{5+\sqrt{5}}$ $=\frac{{(5+\sqrt{5})}^2+{(5-\sqrt{5})}^2}{(5+\sqrt{5})(5-\sqrt{5})}$

$=\frac{25+10\sqrt{5}+5+25-10\sqrt{5}+5}{25-5}$ $=\frac{60}{20}=3$  

d)

$\frac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\frac{\sqrt{3}}{\sqrt{\sqrt{3}+1}+1}$

$=\frac{\sqrt{3}(\sqrt{\sqrt{3}+1}+1)-\sqrt{3}(\sqrt{\sqrt{3}+1}-1)}{(\sqrt{\sqrt{3}+1}+1)(\sqrt{\sqrt{3}+1}-1)}$

$\begin{array}{rl}& =\frac{\sqrt{3(\sqrt{3}+1)}+\sqrt{3}-\sqrt{3(\sqrt{3}+1)}+\sqrt{3}}{\sqrt{3}+1-1}\\ & =\frac{2\sqrt{3}}{\sqrt{3}}=2\end{array}$

Bài 71 trang 16 SBT Toán 9 tập 1: Chứng minh đẳng thức: 

$\sqrt{n+1}-\sqrt{n}=\frac{1}{\sqrt{n+1}+\sqrt{n}}$ với $n$ là số tự nhiên.  

Phương pháp giải:

Áp dụng: 

$\frac{A}{\sqrt{B}\pm \sqrt{C}}=\frac{A(\sqrt{B}\mp \sqrt{C})}{B-C}$ với $B,C\ge 0;B\ne C$.

Lời giải:

Ta có: 

$VP=\frac{1}{\sqrt{n+1}+\sqrt{n}}$ $=\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$

$=\frac{\sqrt{n+1}-\sqrt{n}}{{(\sqrt{n+1})}^2-{(\sqrt{n})}^2}$

$=\frac{\sqrt{n+1}-\sqrt{n}}{n+1-n}$$=\sqrt{n+1}-\sqrt{n}=VT$

(với $n$ là số tự nhiên) 

Vế trái bằng vế phải nên đẳng thức được chứng minh. 

Bài 72 trang 17 SBT Toán 9 tập 1: Xác định giá trị biểu thức sau theo cách thích hợp: 

$\frac{1}{\sqrt{2}+\sqrt{1}}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}$ 

Phương pháp giải:

Áp dụng: 

$\frac{A}{\sqrt{B}\pm \sqrt{C}}=\frac{A(\sqrt{B}\mp \sqrt{C})}{B-C}$ với $B,C\ge 0;B\ne C$.

Lời giải:

Ta có: 

$\frac{1}{\sqrt{2}+\sqrt{1}}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}$

$=\frac{\sqrt{2}-\sqrt{1}}{(\sqrt{2}+\sqrt{1})(\sqrt{2}-\sqrt{1})}$$+\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2)}(\sqrt{3}-\sqrt{2})}$$+\frac{\sqrt{4}-\sqrt{3}}{(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})}$

$=\frac{\sqrt{2}-\sqrt{1}}{2-1}$$+\frac{\sqrt{3}-\sqrt{2}}{3-2}$$+\frac{\sqrt{4}-\sqrt{3}}{4-3}$

$=\sqrt{2}-\sqrt{1}+\sqrt{3}-\sqrt{2}$$+\sqrt{4}-\sqrt{3}$

$=-\sqrt{1}+\sqrt{4}$$=-1+2=1$

Bài 73 trang 17 SBT Toán 9 tập 1: So sánh (không dùng bảng số hay máy tính bỏ túi).  

$\sqrt{2005}-\sqrt{2004}$ với $\sqrt{2004}-\sqrt{2003}$  

Phương pháp giải:

Áp dụng: 

$\frac{1}{\sqrt{A}+\sqrt{B}}$$=\frac{\sqrt{A}-\sqrt{B}}{A-B}\left(A,B\ge 0;A\ne B\right)$

Lời giải:

Ta có: $\frac{1}{\sqrt{2005}+\sqrt{2004}}$ $=\frac{\sqrt{2005}-\sqrt{2004}}{(\sqrt{2005}+\sqrt{2004})(\sqrt{2005}-\sqrt{2004})}$ 

$=\frac{\sqrt{2005}-\sqrt{2004}}{2005-2004}$$=\sqrt{2005}-\sqrt{2004}(1)$ 

Ta có: 

$\frac{1}{\sqrt{2004}+\sqrt{2003}}$ $=\frac{\sqrt{2004}-\sqrt{2003}}{(\sqrt{2004}+\sqrt{2003})(\sqrt{2004}-\sqrt{2003})}$

$=\frac{\sqrt{2004}-\sqrt{2003}}{2004-2003}$$=\sqrt{2004}-\sqrt{2003}(2)$

Vì $\sqrt{2005}+\sqrt{2004}>$$\sqrt{2004}+\sqrt{2003}$ nên:

$\frac{1}{\sqrt{2005}+\sqrt{2004}}<\frac{1}{\sqrt{2004}+\sqrt{2003}}$ (3)

Từ (1), (2), (3) suy ra: 

$\sqrt{2005}-\sqrt{2004}$ < $\sqrt{2004}-\sqrt{2003}$

Bài 74 trang 17 SBT Toán 9 tập 1: Rút gọn: 

$\frac{1}{\sqrt{1}-\sqrt{2}}-\frac{1}{\sqrt{2}-\sqrt{3}}+\frac{1}{\sqrt{3}-\sqrt{4}}$ $-\frac{1}{\sqrt{4}-\sqrt{5}}+\frac{1}{\sqrt{5}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{7}}$ $+\frac{1}{\sqrt{7}-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{9}}$   

Phương pháp giải:

Áp dụng:

$\frac{1}{\sqrt{A}-\sqrt{B}}$$=\frac{\sqrt{A}+\sqrt{B}}{A-B}\left(A,B\ge 0;A\ne B\right)$

Lời giải:

Ta có: 

$\frac{1}{\sqrt{1}-\sqrt{2}}-\frac{1}{\sqrt{2}-\sqrt{3}}+\frac{1}{\sqrt{3}-\sqrt{4}}$

 $-\frac{1}{\sqrt{4}-\sqrt{5}}+\frac{1}{\sqrt{5}-\sqrt{6}}-\frac{1}{\sqrt{6}-\sqrt{7}}$

 $+\frac{1}{\sqrt{7}-\sqrt{8}}-\frac{1}{\sqrt{8}-\sqrt{9}}$ 

$=\frac{\sqrt{1}+\sqrt{2}}{{(\sqrt{1})}^2-{(\sqrt{2})}^2}-\frac{\sqrt{2}+\sqrt{3}}{{(\sqrt{2})}^2-{(\sqrt{3})}^2}$

 $+\frac{\sqrt{3}+\sqrt{4}}{{\left(\sqrt{3}\right)}^2-{\left(\sqrt{4}\right)}^2}-\frac{\sqrt{4}+\sqrt{5}}{{\left(\sqrt{4}\right)}^2-{\left(\sqrt{5}\right)}^2}$

$+\frac{\sqrt{5}+\sqrt{6}}{{(\sqrt{5})}^2-{(\sqrt{6})}^2}-\frac{\sqrt{6}+\sqrt{7}}{{(\sqrt{6})}^2-{(\sqrt{7})}^2}$

 $+\frac{\sqrt{7}+\sqrt{8}}{{(\sqrt{7})}^2-{(\sqrt{8})}^2}-\frac{\sqrt{8}+\sqrt{9}}{{(\sqrt{8})}^2-{(\sqrt{9})}^2}$ 

$=\frac{\sqrt{1}+\sqrt{2}}{1-2}-\frac{\sqrt{2}+\sqrt{3}}{2-3}+\frac{\sqrt{3}+\sqrt{4}}{3-4}$

 $-\frac{\sqrt{4}+\sqrt{5}}{4-5}+\frac{\sqrt{5}+\sqrt{6}}{5-6}-\frac{\sqrt{6}+\sqrt{7}}{6-7}$

 $+\frac{\sqrt{7}+\sqrt{8}}{7-8}-\frac{\sqrt{8}+\sqrt{9}}{8-9}$ 

$=\frac{\sqrt{1}+\sqrt{2}}{-1}-\frac{\sqrt{2}+\sqrt{3}}{-1}+\frac{\sqrt{3}+\sqrt{4}}{-1}$

 $-\frac{\sqrt{4}+\sqrt{5}}{-1}+\frac{\sqrt{5}+\sqrt{6}}{-1}-\frac{\sqrt{6}+\sqrt{7}}{-1}$

 $+\frac{\sqrt{7}+\sqrt{8}}{-1}-\frac{\sqrt{8}+\sqrt{9}}{-1}$ 

$=\frac{\sqrt{1}-\sqrt{9}}{-1}$

$=\sqrt{9}-\sqrt{1}=3-1=2$   

Bài 75 trang 17 SBT Toán 9 tập 1: Rút gọn các biểu thức:

a) $\frac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}$ với  $x\ge 0,y\ge 0$ và  $x\ne y$

b) $\frac{x-\sqrt{3x}+3}{x\sqrt{x}+3\sqrt{3}}$ với $x\ge 0$ 

Phương pháp giải:

Áp dụng hằng đẳng thức: 

$a^3-b^3=(a-b)(a^2+ab+b^2)$

$a^3+b^3=(a+b)(a^2-ab+b^2)$

Lời giải:

a)

Với $x\ge 0,y\ge 0$ và $x\ne y,$ ta có: 

$\frac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=\frac{\sqrt{x^3}-\sqrt{y^3}}{\sqrt{x}-\sqrt{y}}$
$=\frac{(\sqrt{x}-\sqrt{y})(x+\sqrt{xy}+y)}{\sqrt{x}-\sqrt{y}}$

$=x+\sqrt{xy}+y$ 

 b)

Với $x\ge 0,$ ta có:

$\begin{array}{rl}& \frac{x-\sqrt{3x}+3}{x\sqrt{x}+3\sqrt{3}}=\frac{x-\sqrt{3x}+3}{\sqrt{x^3}+\sqrt{3^3}}\\ & =\frac{x-\sqrt{3x}+3}{(\sqrt{x}+\sqrt{3})(x-\sqrt{3x}+3)}\\ & =\frac{1}{\sqrt{x}+\sqrt{3}}\end{array}$

Bài 76 trang 17 SBT Toán 9 tập 1: Trục căn thức ở mẫu:

a) $\frac{1}{\sqrt{3}+\sqrt{2}+1}$

b) $\frac{1}{\sqrt{5}-\sqrt{3}+2}$  

Phương pháp giải:

Áp dụng: 

$\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}$ 

$\frac{A}{\sqrt{B}\pm C}=\frac{A(\sqrt{B}\mp C)}{B-C^2}$

(trong điều kiện các biểu thức có nghĩa)

Lời giải:

a)

$\begin{array}{rl}& \frac{1}{\sqrt{3}+\sqrt{2}+1}=\frac{1}{\sqrt{3}+(\sqrt{2}+1)}\\ & =\frac{\sqrt{3}-(\sqrt{2}+1)}{\left[\sqrt{3}+(\sqrt{2}+1)\right]\left[\sqrt{3}-(\sqrt{2}+1)\right]}\end{array}$

$=\frac{\sqrt{3}-\sqrt{2}-1}{3-{(\sqrt{2}+1)}^2}=\frac{\sqrt{3}-\sqrt{2}-1}{3-(2+2\sqrt{2}+1)}$ $=\frac{\sqrt{3}-\sqrt{2}-1}{-2\sqrt{2}}$ 

$=\frac{-\sqrt{2}(\sqrt{3}-\sqrt{2}-1)}{2{(\sqrt{2})}^2}$ $=\frac{-\sqrt{6}+2+\sqrt{2}}{4}$ 

 b)

$\frac{1}{\sqrt{5}-\sqrt{3}+2}$ $=\frac{1}{\sqrt{5}-(\sqrt{3}-2)}$$=\frac{\sqrt{5}+(\sqrt{3}-2)}{\left[\sqrt{5}-(\sqrt{3}-2)\right]\left[\sqrt{5}+(\sqrt{3}-2)\right]}$ 

$=\frac{\sqrt{5}+\sqrt{3}-2}{5-{(\sqrt{3}-2)}^2}$ $=\frac{\sqrt{5}+\sqrt{3}-2}{5-(3-4\sqrt{3}+4)}$ $=\frac{\sqrt{5}+\sqrt{3}-2}{4\sqrt{3}-2}$  

$=\frac{\sqrt{5}+\sqrt{3}-2}{2(2\sqrt{3}-1)}$ $=\frac{(\sqrt{5}+\sqrt{3}-2)(2\sqrt{3}+1)}{2\left[(2\sqrt{3}-1)(2\sqrt{3}+1)\right]}$ 

$=\frac{2\sqrt{15}+\sqrt{5}+6+\sqrt{3}-4\sqrt{3}-2}{2(12-1)}$
$=\frac{2\sqrt{15}+\sqrt{5}+4-3\sqrt{3}}{22}$

Bài 77 trang 17 SBT Toán 9 tập 1: Tìm $x$, biết: 

a) $\sqrt{2x+3}=1+\sqrt{2}$

b) $\sqrt{10+\sqrt{3}x}=2+\sqrt{6}$

c) $\sqrt{3x-2}=2-\sqrt{3}$

d) $\sqrt{x+1}=\sqrt{5}-3$ 

Phương pháp giải:

Áp dụng:

$\sqrt{A}=m\iff A=m^2$  (với $m\ge 0$) 

Lời giải:

a)

$\sqrt{2x+3}=1+\sqrt{2}$

$\begin{array}{l}\iff 2x+3=(1+\sqrt{2}{)}^2\\ \iff 2x+3=1+2\sqrt{2}+2\end{array}$

$\iff 2x=2\sqrt{2}\iff x=\sqrt{2}$

Vậy $x=\sqrt{2}$

 b)

$\sqrt{10+\sqrt{3}x}=2+\sqrt{6}$

$\iff 10+\sqrt{3}x=(2+\sqrt{6}{)}^2$

$\iff 10+\sqrt{3}x=4+4\sqrt{6}+6$$\iff \sqrt{3}x=4\sqrt{6}$

$\iff x=\frac{4\sqrt{6}}{\sqrt{3}}\iff x=4\sqrt{2}$ 

Vậy $x=4\sqrt{2}$

 c)

$\sqrt{3x-2}=2-\sqrt{3}$

$\begin{array}{l}\iff 3x-2=(2-\sqrt{3}{)}^2\\ \iff 3x-2=4-4\sqrt{3}+3\end{array}$

$\iff 3x=9-4\sqrt{3}\iff x=\frac{9-4\sqrt{3}}{3}$

Vậy $x=\frac{9-4\sqrt{3}}{3}$

 d)

$\sqrt{x+1}=\sqrt{5}-3$

Ta có:

$\sqrt{5}<\sqrt{9}$ $\iff \sqrt{5}<3\iff \sqrt{5}-3<0$

Không có giá trị nào của $x$ để $\sqrt{x+1}=\sqrt{5}-3$.

Bài 78 trang 17 SBT Toán 9 tập 1: Tìm tập hợp các giá trị $x$ thỏa mãn điều kiện sau và biểu diễn tập hợp đó trên trục số:

a) $\sqrt{x-2}\ge \sqrt{3}$

b) $\sqrt{3-2x}\le \sqrt{5}$ 

Phương pháp giải:

Áp dụng:

Với $A\ge 0;B\ge 0$ ta có: 

$\sqrt{A}\ge \sqrt{B}\iff A\ge B$ 

Lời giải:

a)

Điều kiện: $x-2\ge 0\iff x\ge 2$

Ta có: $\sqrt{x-2}\ge \sqrt{3}\iff x-2\ge 3\iff x\ge 5$

Giá trị $x\ge 5$ thỏa mãn điều kiện. 

b)

Điều kiện: $3-2x\ge 0\iff 3\ge 2x\iff x\le 1,5$

Ta có:  

$\sqrt{3-2x}\le \sqrt{5}\iff 3-2x\le 5$

$\iff -2x\le 2\iff x\ge -1$

Kết hợp với điều kiện ta có: $-1\le x\le 1,5$

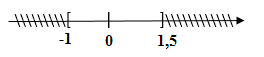
Bài 79 trang 17 SBT Toán 9 tập 1: Cho các số $x$ và $y$ có dạng: $x=a_1\sqrt{2}+b_1$ và $x=a_2\sqrt{2}+b_2$, trong đó $a_1,a_2,b_1,b_2$ là các số hữu tỉ. Chứng minh: 

a)  $x+y$ và $x.y$ cũng có dạng $a\sqrt{2}+b$ với $a$ và $b$ là số hữu tỉ.

b) $\frac{x}{y}$ với $y\ne 0$ cũng có dạng $a\sqrt{2}+b$ với $a$ và $b$ là số hữu tỉ.   

Phương pháp giải:

Biến đổi, nhóm các hạng tử để đưa về dạng $a\sqrt{2}+b$ với $a$ và $b$ là số hữu tỉ.

Với $B>0$ ta có: $\frac{A}{\sqrt{B}}=\frac{A\sqrt{B}}{B}$ 

Với $B\ge 0,B\ne C^2$ ta có: $\frac{A}{\sqrt{B}\pm C}=\frac{A(\sqrt{B}\mp C)}{B-C^2}$

Lời giải:

a)

Ta có: 

$x+y=(a_1\sqrt{2}+b_1)+(a_2\sqrt{2}+b_2)$

$=(a_1+a_2)\sqrt{2}+(b_1+b_2)$

Vì $a_1,a_2,b_1,b_2$ là các số hữu tỉ nên $a_1+a_2,b_1+b_2$ cũng là số hữu tỉ.

Lại có: 

$xy=(a_1\sqrt{2}+b_1)(a_2\sqrt{2}+b_2)$

$=2a_1{a}_2+a_1{b}_2\sqrt{2}+a_2{b}_1\sqrt{2}+b_1{b}_2$

$=(a_1{b}_2+a_2{b}_1)\sqrt{2}+(2a_1{a}_2+b_1{b}_2)$

Vì $a_1,a_2,b_1,b_2$ là các số hữu tỉ nên $a_1{b}_2+a_2{b}_1$, $2a_1{a}_2+b_1{b}_2$ cũng là số hữu tỉ. 

b)

Ta có:

$\begin{array}{rl}& \frac{x}{y}=\frac{a_1\sqrt{2}+b_1}{a_2\sqrt{2}+b_2}\\ & =\frac{(a_1\sqrt{2}+b_1)(a_2\sqrt{2}-b_2)}{{(a_2\sqrt{2})}^2-{b_2}^2}\end{array}$

$=\frac{2a_1{a}_2-a_1{b}_2\sqrt{2}+a_2{b}_1\sqrt{2}-b_1{b}_2}{2{a_2}^2-{b_2}^2}$

$=\frac{a_2{b}_1\sqrt{2}-a_1{b}_2\sqrt{2}+2a_1{a}_2-b_1{b}_2}{2{a_2}^2-{b_2}^2}$

$=\sqrt{2}\frac{a_2{b}_1-a_1{b}_2}{2{a_2}^2-{b_2}^2}+\frac{2a_1{a}_2-b_1{b}_2}{2{a_2}^2-{b_2}^2}$

Vì $y\ne 0$ nên $a_2$ và $b_2$ không đồng thời bằng 0 

Suy ra: $2{a_2}^2-{b_2}^2$ $\ne 0$

(Nếu $2{a_2}^2-{b_2}^2=0$ thì  $\sqrt{2}=\frac{b_2}{a_2}$  

Điều này mâu thuẫn với $\sqrt{2}$ là số vô tỉ)

Vậy $\frac{a_2{b}_1-a_1{b}_2}{2{a_2}^2-{b_2}^2}$; $\frac{2a_1{a}_2-b_1{b}_2}{2{a_2}^2-{b_2}^2}$ đều là số hữu tỉ. 

Bài tập bổ sung (trang 18 SBT Toán 9)

Bài 7.1 trang 18 SBT Toán 9 tập 1: Với $x<0;y<0$ biểu thức $x\sqrt{\frac{x}{y^3}}$ được biến đổi thành

(A) $\frac{x}{y^3}\sqrt{xy}$

(B) $\frac{x}{y}\sqrt{xy}$

(C) $-\frac{x}{y^3}\sqrt{xy}$

(D) $-\frac{x}{y}\sqrt{xy}$  

Hãy chọn đáp án đúng. 

Phương pháp giải:

Áp dụng: 

Với $A\ge 0;B>0$

$\sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}$

Lời giải:

Ta có: 

$x\sqrt{\frac{x}{y^3}}=x\sqrt{\frac{xy}{y^4}}$

Do $x<0;y<0$ nên $xy>0$

$x\sqrt{\frac{xy}{y^4}}=x\frac{\sqrt{xy}}{\sqrt{y^4}}=\frac{x}{y^2}\sqrt{xy}$

Vậy chọn đáp án (A).

Bài 7.2 trang 18 SBT Toán 9 tập 1: Giá trị của $\frac{6}{\sqrt{7}-1}$ bằng 

(A) $\sqrt{7}-1$

(B) $1-\sqrt{7}$

(C) $-\sqrt{7}-1$

(D) $\sqrt{7}+1$

Hãy chọn đáp án đúng. 

Phương pháp giải:

Áp dụng: Với $B\ge 0;B\ne C^2,$ ta có:

$\frac{A}{\sqrt{B}\pm C}=\frac{A(\sqrt{B}\mp C)}{B-C^2}$ 

Lời giải:

Ta có:

$\frac{6}{\sqrt{7}-1}=\frac{6.(\sqrt{7}+1)}{{\left(\sqrt{7}\right)}^2-1^2}$$=\frac{6.\left(\sqrt{7}+1\right)}{6}=\sqrt{7}+1$

Vậy đáp án (D)