Tài liệu Bài tập Góc nội tiếp hình học toán 9 gồm các nội dung chính sau:
I. Phương pháp giải
– tóm tắt lý thuyết ngắn gọn.
II. Bài tập
– gồm 12 bài tập vận dụng có đáp án và lời giải chi tiết giúp học sinh tự rèn luyện cách giải các dạng Bài tập Góc nội tiếp hình học toán 9.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BÀI TẬP GÓC NỘI TIẾP
I. Phương pháp giải
1.Định nghĩa góc nội tiếp
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó. Cung nằm giữa hai cạnh của góc được gọi là cung bị chắn
Một góc muốn được công nhận là góc nội tiếp đường tròn thì góc đó phải đạt được hai yêu cầu
*Yêu cầu 1 : Đỉnh của góc phải nằm trên đường tròn
*Yêu cầu 2: Hai cạnh của góc phải chứa hai dây cung của đường tròn đó
Ví dụ ở các hình vẽ sau :
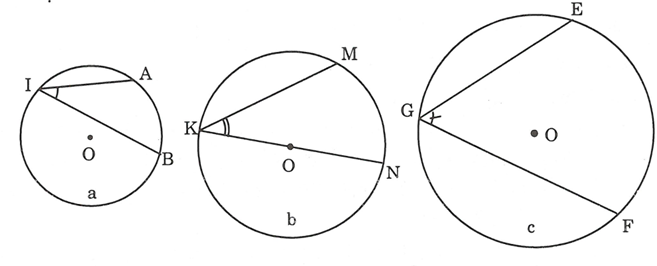
Các góc ở các hình a, b, c là các góc nội tiếp
Các góc ở các hình từ 1 đến 6 không phải là các góc nội tiếp và không đạt đủ hai yêu cầu của góc nội tiếp đường tròn
2.Định lí
Trong một đường tròn số đo của góc nội tiếp bằng nửa số đo của cung bị chắn
3.Hệ quả :Trong một đường tròn:
a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau
c) Các góc nội tiếp (nhỏ hơn hoặc bằng ) có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung
d) Góc nội tiếp chắn nửa đường tròn là góc vuông
II. Bài tập
Bài 1: (15/75/SGK T2)
Các khẳng định sau đây đúng hay sai ?
a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau
b) Trong một đường tròn các góc nội tiếp bằng nhau thì cùng chắn một cung
Giải
a) Khẳng định ở câu a) là khẳng định đúng (theo hệ quả 2)
b) Khẳng định ở câu b) là khẳng định sai.Ví dụ : Tam giác cân nội tiếp đường tròn có hai góc nội tiếp bằng nhau nhưng chắn hai cung khác nhau (hai cung này có số đo bằng nhau)
Bài 2: (16/75/SGK T2)
Xem hình 19 ( Hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C)
a) Biết . Tính
b) Nếu thì có số đo là bao nhiêu ?
Xem thêm