Giải SGK Toán 9 Bài tập ôn cuối năm

Giải bài tập Toán lớp 9 Bài tập ôn cuối năm

A. Phần đại số

Bài 1 trang 131 SGK Toán lớp 9 tập 2: Xét các mệnh đề sau:

Những mệnh đề nào là sai?

Hãy chọn câu trả lời đúng trong các câu A, B, C, D dưới đây:

A. Chỉ có mệnh đề I sai;

B. Chỉ có mệnh đề II sai;

C. Các mệnh đề I và IV sai;

D. Không có mệnh đề nào sai.

Lời giải:

Mệnh đề I sai vì không có căn bậc hai của số âm

Mệnh đề IV sai vì $\sqrt{100}=10$ (căn bậc hai số học)

Các mệnh đề II, III là đúng

Vậy ta chọn đáp án C.

Bài 2 trang 131 SGK Toán lớp 9 tập 2: Rút gọn các biểu thức:

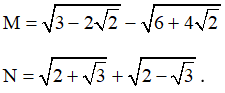
Lời giải:

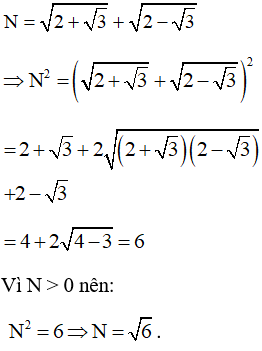
Bài 3 trang 132 SGK Toán lớp 9 tập 2: Giá trị của biểu thức $\frac{2\left(\sqrt{2}+\sqrt{6}\right)}{3\sqrt{2+\sqrt{3}}}$ bằng:

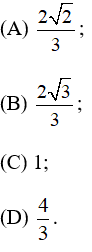
Hãy chọn câu trả lời đúng.

Lời giải:

Ta có:

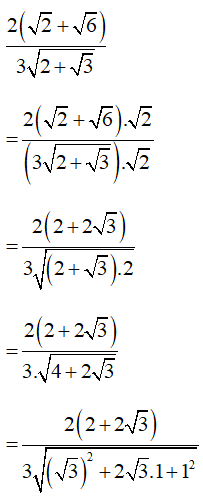
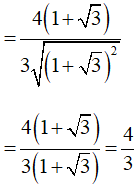
Vậy ta chọn đáp án D.

Bài 4 trang 132 SGK Toán lớp 9 tập 2: Nếu $\sqrt{2+\sqrt{x}}=3$ thì x bằng:

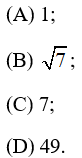
Hãy chọn câu trả lời đúng.

Lời giải:

Điều kiện xác định của biểu thức ta có: $x\ge 0$

Ta có:

$\sqrt{2+\sqrt{x}}=3$

$\iff {\left(\sqrt{2+\sqrt{x}}\right)}^2=3^2$ (do hai vế đều dương)

$\iff 2+\sqrt{x}=9\iff \sqrt{x}=7$

$\iff {\left(\sqrt{x}\right)}^2=7^2$ (do hai vế đều dương)

$\iff x=49$ (thỏa mãn điều kiện)

Vậy ta chọn đáp án (D)

Bài 5 trang 132 SGK Toán lớp 9 tập 2: Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào biến: 

$\left(\frac{2+\sqrt{x}}{x+2\sqrt{x}+1}-\frac{\sqrt{x}-2}{x-1}\right).$$\frac{x\sqrt{x}+x-\sqrt{x}-1}{\sqrt{x}}$

Lời giải:

$\left(\frac{2+\sqrt{x}}{x+2\sqrt{x}+1}-\frac{\sqrt{x}-2}{x-1}\right).$$\frac{x\sqrt{x}+x-\sqrt{x}-1}{\sqrt{x}}$

(Điều kiện: $x\ge 0, x\ne 1$)

$=\left[\frac{2+\sqrt{x}}{{\left(\sqrt{x}+1\right)}^2}-\frac{\sqrt{x}-2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right].\frac{x\left(\sqrt{x}+1\right)-\left(\sqrt{x}+1\right)}{\sqrt{x}}$

$=$$\frac{\left(2+\sqrt{x}\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{{\left(\sqrt{x}+1\right)}^2\left(\sqrt{x}-1\right)}$$.\frac{\left(\sqrt{x}+1\right)\left(x-1\right)}{\sqrt{x}}$

$=\frac{x+\sqrt{x}-2-\left(x-\sqrt{x}-2\right)}{\left(\sqrt{x}+1\right)\left(x-1\right)}.\frac{\left(x-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}$

$=\frac{x+\sqrt{x}-2-x+\sqrt{x}+2}{\sqrt{x}}=\frac{2\sqrt{x}}{\sqrt{x}}=2$

Vậy giá trị của biểu thức đã cho luôn bằng 2 và không phụ thuộc cái giá trị của biến x.

Bài 6 trang 132 SGK Toán lớp 9 tập 2:Cho hàm số y = ax + b. Tìm a và b, biết rằng đồ thị của hàm số đã cho thỏa mãn một trong các điều kiện sau:

a) Đi qua hai điểm A(1; 3) và B(– 1; –1).

b) Song song với đường thẳng y = x + 5 và đi qua điểm C(1; 2).

Lời giải:

a)

Gọi (d) là độ thị hàm số y = ax + b

Vì A (1; 3) thuộc (d) nên ta có: 3 = a + b

Vì B (–1; –1) thuộc (d) nên ta có: –1 = –a + b

Ta có hệ phương trình:

$\left\{\begin{array}{l}a+b=3\\ -a+b=-1\end{array}\right.\iff \left\{\begin{array}{l}a+b+(-a)+b=3+(-1)\\ a+b=3\end{array}\right.\iff \left\{\begin{array}{l}2b=2\\ a=3-b\end{array}\right.\iff \left\{\begin{array}{l}b=1\\ a=2\end{array}\right.$

Vậy a = 2; b = 1.

b)

Gọi (d) là độ thị hàm số y = ax + b

Vì (d) song song với (d’): y = x + 5 nên ta có: a = 1, b$\ne$5

Ta được (d): y = x + b

Vì C(1; 2) thuộc (d) nên ta có: 2 = 1 + b $\iff$ b = 1 (thỏa mãn)

Vậy a = 1; b = 1.

Bài 7 trang 132 SGK Toán lớp 9 tập 2: Cho hai đường thẳng:

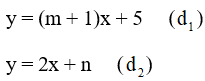
Với giá trị nào của m và n thì:

Lời giải:

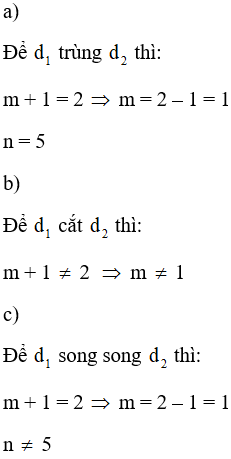
Bài 8 trang 132 SGK Toán lớp 9 tập 2: Chứng minh rằng khi k thay đổi, các đường thẳng (k + 1)x – 2y = 1 luôn đi qua một điểm cố định. Tìm điểm cố định đó.

Lời giải:

Khi x = 0 thì ta có: (k + 1).0 – 2y = 1  $\Rightarrow y=\frac{-1}{2}$

Do đó, các đường thẳng (k + 1)x – 2y = 1 luôn đi qua một điểm cố định là $\left(0;\frac{-1}{2}\right)$ với mọi số thực k.

Bài 9 trang 133 SGK Toán lớp 9 tập 2: Giải các hệ phương trình:

Lời giải:

a)

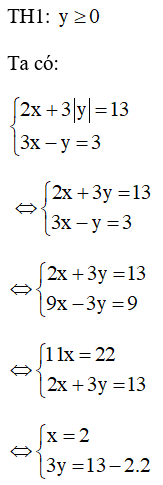
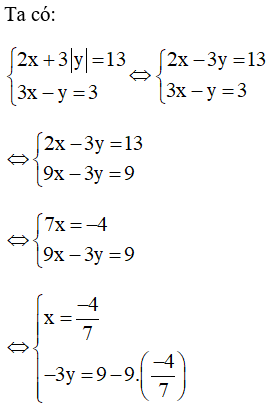
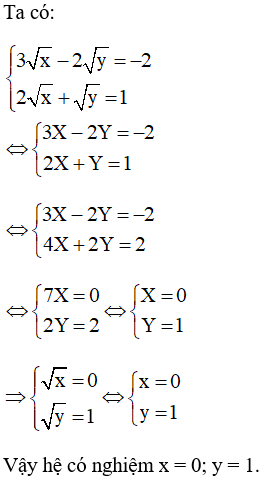
Bài 10 trang 133 SGK Toán lớp 9 tập 2: Giải các hệ phương trình:

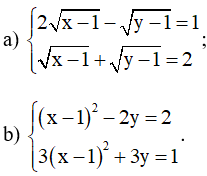
Lời giải:

a)

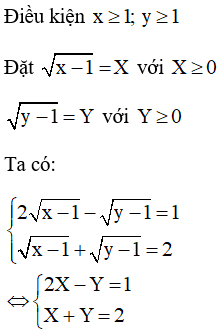
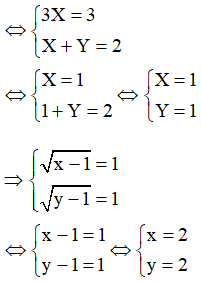
Vậy hệ có nghiệm x = 2; y = 2.

b)

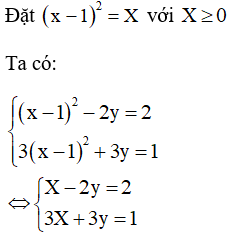
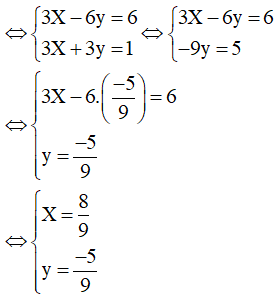
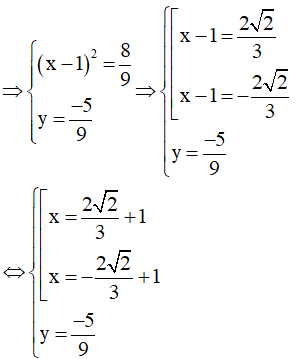
Vậy hệ phương trình có nghiệm $\left\{\begin{array}{l}{x}_1=1+\frac{2\sqrt{2}}{3}\\ y_1=\frac{-5}{9}\end{array}\right.$ và $\left\{\begin{array}{l}{x}_2=1-\frac{2\sqrt{2}}{3}\\ y_2=\frac{-5}{9}\end{array}\right.$.

Bài 11 trang 133 SGK Toán lớp 9 tập 2: Hai giá sách có 450 cuốn. Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ hai sẽ bằng $\frac{4}{5}$ số sách ở giá thứ nhất. Tính số sách lúc đầu trong mỗi giá.

Lời giải:

Gọi số sách ở giá thứ nhất là x ( cuốn)

Số sách ở giá thứ hai là y (cuốn), (x, y $\in {\mathrm{\mathbb{N}}}^{*}$ ; x > 50, x < 450, y < 450)

Hai giá sách có tất cả 450 cuốn nên ta có:  x+ y = 450 (1)

Khi chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ nhất khi đó là x – 50 và số sách ở giá thứ hai là y + 50

Theo đề bài nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách ở giá thứ hai sẽ bằng $\frac{4}{5}$ số sách ở giá thứ nhất, nên ta có:

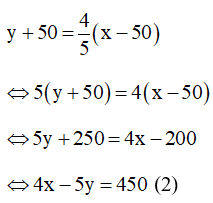
Từ (1) và (2) ta có hệ phương trình:

$\begin{array}{l}\left\{\begin{array}{l}x+y=450\\ 4x-5y=450\end{array}\right.\\ \iff \left\{\begin{array}{l}4x+4y=1800\\ 4x-5y=450\end{array}\right.\\ \iff \left\{\begin{array}{l}9y=1350\\ x+y=450\end{array}\right.\\ \iff \left\{\begin{array}{l}y=150\\ x=300\end{array}\right.\end{array}$

Vậy số sách ở giá thứ nhất là 300 quyển, giá thứ hai là 150 quyển.

Bài 12 trang 133 SGK Toán lớp 9 tập 2: Quãng đường AB gồm một đoạn lên dốc dài 4km và một đoạn xuống dốc dài 5km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc, xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.

Lời giải:

Gọi vận tốc lúc lên dốc và lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)

Lúc đi từ A đến B: Đoạn lên dốc dài 4km và đoạn xuống dốc dài 5km

Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km

Thời gian đi lên dốc là $\frac{4}{x}$( h) , thời gian xuống dốc là: $\frac{5}{y}$ (h)

Theo đề bài thời gian đi A đến B là 40 phút = $\frac{2}{3}\mathrm{h}$ nên ta có:

$\frac{4}{x}+\frac{5}{y}=\frac{2}{3}$  (1)

Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km

Thời gian đi lên dốc là $\frac{5}{x}$ (h), thời gian xuống dốc là $\frac{4}{y}$ (h)

Theo đầu bài thời gian đi A đến B là 41 phút = $\frac{41}{60}h$ nên ta có:

$\frac{5}{x}+\frac{4}{y}=\frac{41}{60}$ (2)

Từ (1) và (2) ta có hệ phương trình:

$\left\{\begin{array}{l}\frac{4}{x}+\frac{5}{y}=\frac{2}{3}\\ \frac{5}{x}+\frac{4}{y}=\frac{41}{60}\end{array}\right.$

Đặt $X=\frac{1}{x};Y=\frac{1}{y}$, hệ phương trình trở thành:

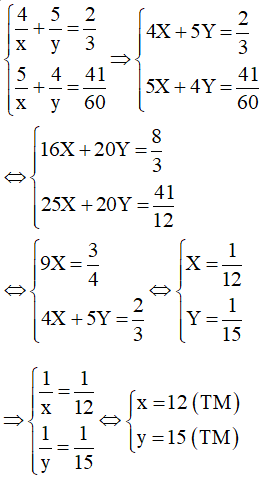
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

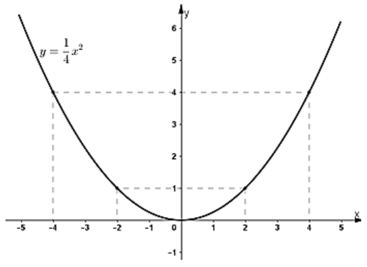
Bài 13 trang 133 SGK Toán lớp 9 tập 2: Xác định hệ số a của hàm $y=a{x}^2$, biết rằng đồ thị của nó đi qua điểm A(–2; 1).Vẽ đồ thị của hàm số đó.

Lời giải:

Đồ thị hàm số $y=a{x}^2$ đi qua A (–2; 1) nên ta có:

$1=a{\left(-2\right)}^2\iff 4a=1\iff a=\frac{1}{4}$

Vậy hàm số cần vẽ đồ thị là:

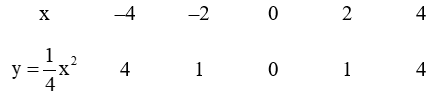
Bài 14 trang 133 SGK Toán lớp 9 tập 2: Gọi $x_1,x_2$ là hai nghiệm của phương trình $3x^2-ax-b=0$. Tổng $x_1+x_2$ bằng:

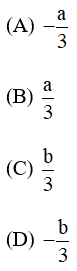
Hãy chọn câu trả lời đúng.

Lời giải:

Xét phương trình $3x^2-ax-b=0$ có hai nghiệm  $x_1,x_2$

Áp dụng hệ thức Vi–ét ta có: $x_1+x_2=-\left(\frac{-a}{3}\right)=\frac{a}{3}$

Vậy ta chọn đáp án (B)

Bài 15 trang 133 SGK Toán lớp 9 tập 2: Hai phương trình $x^2+ax+1=0$ và $x^2-x-a=0$ có một nghiệm thực chung khi a bằng:

(A) 0 ;    

(B) 1 ;    

(C) 2 ;    

(D) 3

Hãy chọn câu trả lời đúng.

Lời giải:

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:

Thay a = –1 vào phương trình $x^2-x-a=0$ ta có: $x^2-x+1=0$

Phương trình này vô nghiệm nên ta loại a = –1

Thay x = –1 vào phương trình $x^2-x-a=0$ ta có:

${(-1)}^2-(-1)+a=0\Rightarrow a=2$

Vậy với a = 2 thì phương trình có nghiệm chung là x = – 1

Vậy ta chọn đáp án (C)

Bài 16 trang 133 SGK Toán lớp 9 tập 2: Giải các phương trình:

a) $2x^3-x^2+3x+6=0$

b) $x(x+1)(x+4)$$(x+5)=12$

Lời giải:

a)

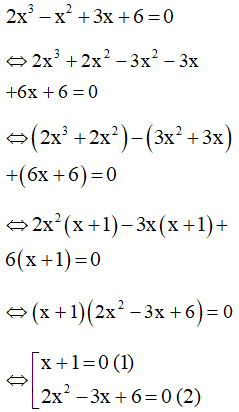
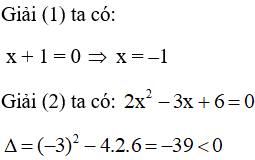
Do đó, (2) vô nghiệm

Vậy $2x^3-x^2+3x+6=0$ có duy nhất một nghiệm x = –1.

b)

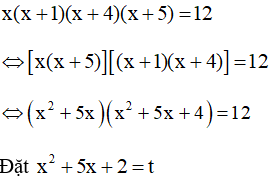
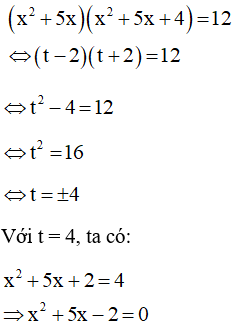
Giải phương trình $x^2+5x-2=0$ có:

$\Delta =5^2-\mathrm{4.1.}(-2)=33$ > 0

Do đó phương trình $x^2+5x-2=0$ có hai nghiệm phân biệt:

$x_1=\frac{-5+\sqrt{33}}{2};x_2=\frac{-5-\sqrt{33}}{2}$

Với y = –4, ta có: 

$x^2+5x+2=-4\Rightarrow x^2+5x+6=0$

Giải phương trình $x^2+5x+6=0$, ta có:

$\Delta =5^2-\mathrm{4.1.6}=1$ > 0

Do đó phương trình $x^2+5x+6=0$ có hai nghiệm phân biệt:

$x_3=\frac{-5+\sqrt{1}}{2}=-2;x_4=\frac{-5-\sqrt{1}}{2}=-3$

Vậy phường trình $x(x+1)(x+4)(x+5)=12$ có tập nghiệm là:

$S=\left\{-2;-3;\frac{-5+\sqrt{33}}{2};\frac{-5+\sqrt{33}}{2}\right\}$

Bài 17 trang 133 SGK Toán lớp 9 tập 2: Một lớp học có 40 học sinh được xếp ngồi đều nhau trên các ghế băng. Nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh. Tính số ghế băng lúc đầu.

Lời giải:

Gọi số ghế băng lúc đầu là x ( ghế băng), ( x $\in {\mathrm{\mathbb{N}}}^{*}$, x > 2)

Số học sinh ngồi trên mỗi ghế là $\frac{40}{x}$ (học sinh)

Khi bớt đi 2 ghế băng thì còn lại x – 2 ( ghế băng) và khi đó, mỗi ghế có $\frac{40}{x-2}$ học sinh ngồi

Theo giả thiết, nếu ta bớt đi 2 ghế băng thì mỗi ghế còn lại phải xếp thêm 1 học sinh nên ta có phương trình:

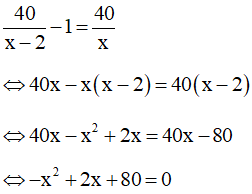
Giải phương trình $-x^2+2x+80=0$ có:

$\Delta =2^2-4.\left(-1\right).80=324$ > 0

Do đó, phương trình $-x^2+2x+80=0$ có hai nghiệm phân biệt:

$x_1=\frac{-2+\sqrt{324}}{2.(-1)}=-8$ (loại)

$x_2=\frac{-2-\sqrt{324}}{2.(-1)}=10$ (TM)

Vậy lúc đầu có 10 ghế băng.

Bài 18 trang 133 SGK Toán lớp 9 tập 2: Cạnh huyền của một tam giác vuông bằng 10cm. Hai cạnh góc vuông có độ dài hơn kém nhau 2cm. Tính độ dài các cạnh góc vuông của tam giác vuông đó.

Lời giải:

Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x (cm), y (cm) ( 0 < y < x < 10)

Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 (1).

Theo định lý Py–ta–go ta có:

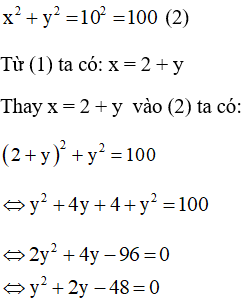
Giải phương trình $y^2+2y-48=0$ có:

$\Delta =2^2-\mathrm{4.1.}(-48)=196$ > 0

Do đó, phương trình $y^2+2y-48=0$ có hai nghiệm phân biệt:

$x_1=\frac{-2+\sqrt{196}}{2.1}=6$ (TM)

$x_2=\frac{-2-\sqrt{196}}{2.1}=-8$ (loại)

Vậy y = 6 $\Rightarrow x=2+y=2+6=8$

Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.

B. Phần hình học

Bài 1 trang 134 SGK Toán lớp 9 tập 2: Chu vi hình chữ nhật ABCD là 20cm. Hãy tìm giá trị nhỏ nhất của độ dài đường chéo AC.

Lời giải:

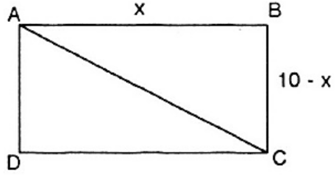
Gọi độ dài một cạnh của hình chữ nhật là x (x > 0, cm)

Nửa chu vi hình chữ nhật là: 20 : 2 = 10 (cm)

Độ dài cạnh còn lại của hình chữ nhật là : 10 – x (cm).

Xét tam giác ABC vuông tại B (do ABCD là hình chữ nhật)

Theo định lý Pytago ta có:

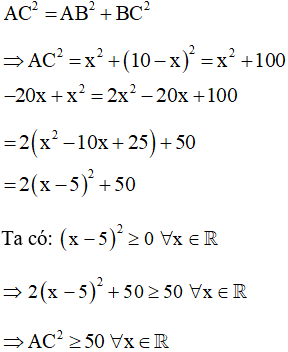
Vậy đường chéo AC nhỏ nhất là $5\sqrt{2}$cm khi ABCD là hình vuông cạnh bằng 5cm.

Bài 2 trang 134 SGK Toán lớp 9 tập 2: Tam giác ABC có $\widehat{B}={45}^o$, góc $\widehat{C}={30}^o$. Nếu AC = 8 thì AB bằng:

Hãy chọn câu trả lời đúng.

Lời giải:

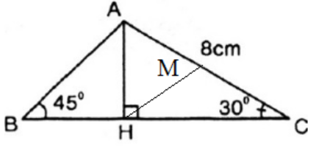
Kẻ AH vuông góc với BC tại H

M là trung điểm của AC

Xét tam giác AHC vuông tại H (do AH vuông góc với BC tại H)

HM là đường trung tuyến ứng với cạnh huyền

$\Rightarrow HM=AM=CM=\frac{1}{2}AC=\frac{1}{2}.8=4$

Xét tam giác AHM có: 

HM = AM (chứng minh trên)

Do đó, tam giác AHM cân tại M

Có: $\widehat{HAM}={60}^o$

Do đó, tam giác AHM đều

$\Rightarrow AH=AM=4$

Xét tam giác AHB vuông tại H (do AH vuông góc với BC tại H)

Có: $\widehat{ABH}={45}^o$

Do đó, tam giác AHB vuông cân tại H

Bài 3 trang 134 SGK Toán lớp 9 tập 2: Cho tam giác ABC vuông ở C có đường trung tuyến BN vuông góc với đường trung tuyến CM, cạnh BC = a. Tính độ dài đường trung tuyến BN.

Lời giải:

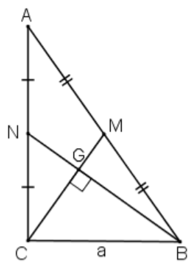
Gọi G là trọng tâm tam giác ABC

$\Rightarrow BG=\frac{2}{3}BN$ (tính chất trọng tâm)

Xét tam giác BCN vuông tại C (do tam giác ABC vuông tại C) có đường cao CG (do CM vuông góc với BN tại G)

Áp dụng hệ thức lượng trong tam giác vuông ta có:

$B{C}^2=BG.BN=\frac{2}{3}BN.BN=\frac{2}{3}B{N}^2\Rightarrow a^2=\frac{2}{3}B{N}^2\Rightarrow B{N}^2=\frac{3}{2}{a}^2\Rightarrow BN=\frac{\sqrt{3}}{\sqrt{2}}a$

Bài 4 trang 134 SGK Toán lớp 9 tập 2: Nếu tam giác ABC vuông tại C và có sinA = $\frac{2}{3}$ thì tanB bằng:

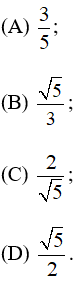
Hãy chọn câu trả lời đúng.

Lời giải:

Xét tam giác ABC vuông tại C

Có:

$\sin A=\frac{BC}{AB}=\frac{2}{3}\Rightarrow AB=\frac{3BC}{2}$

Áp dụng định lý Py–ta–go ta có:

$A{B}^2=A{C}^2+B{C}^2\Rightarrow A{C}^2=A{B}^2-B{C}^2={\left(\frac{3BC}{2}\right)}^2-B{C}^2=\frac{5}{4}B{C}^2\Rightarrow AC=\frac{\sqrt{5}}{2}BC$

Ta  có: $\tan B=\frac{AC}{BC}=\frac{\frac{\sqrt{5}}{2}BC}{BC}=\frac{\sqrt{5}}{2}$

Vậy ta chọn đáp án (D).

Bài 5 trang 134 SGK Toán lớp 9 tập 2: Tam giác ABC vuông tại C có AC = 15cm. Đường cao CH chia AB thành hai đoạn AH và HB. Biết HB = 16cm. Tính diện tích tam giác ABC.

Lời giải:

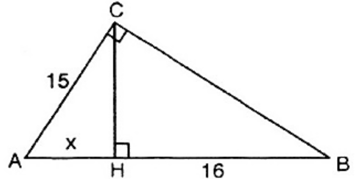
Đặt AH = x (x > 0)

Xét tam giác ABC vuông tại C có đường cao CH

Áp dụng hệ thức lượng trong tam giác vuông ta có:

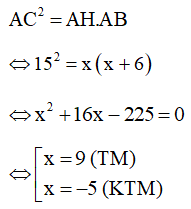
Vậy AH = 9 (cm)

Xét tam giác ACH vuông tại H (do AH là đường cao)

Áp dụng định lý Py–ta–go ta có:

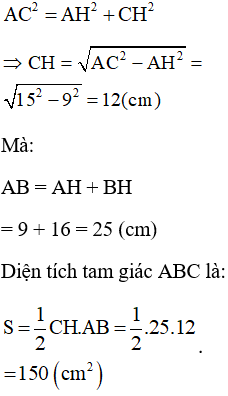
Bài 6 trang 134 SGK Toán lớp 9 tập 2: Một hình chữ nhật cắt đường tròn như hình 121 biết AB = 4, BC = 5, DE = 3 (với cùng đơn vị đo). Độ dài EF bằng:

(A) 6;

(B) 7;

(C) $\frac{20}{3}$;

(D) 8.

Hãy chọn câu trả lời đúng.

Lời giải:

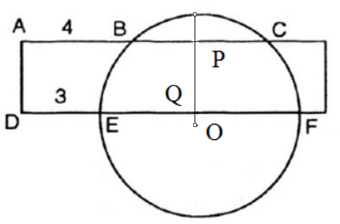
Gọi O là tâm đường tròn. Từ O kẻ bán kính vuông góc với BC, cắt BC ở P, cắt EF ở Q. Ta có:

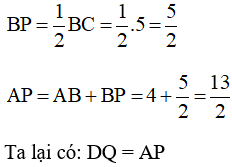
Bài 7 trang 134 SGK Toán lớp 9 tập 2: Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho $\widehat{DOE}={60}^o$.

a) Chứng minh tích BD.CE không đổi.

b) Chứng minh BOD $\backsim$ OED. Từ đó suy ra tia DO là tia phân giác của $\widehat{BDE}$.

c) Vẽ đường tròn tâm O tiếp xúc với AB. Chứng minh rằng đường tròn này luôn tiếp xúc với DE.

Lời giải:

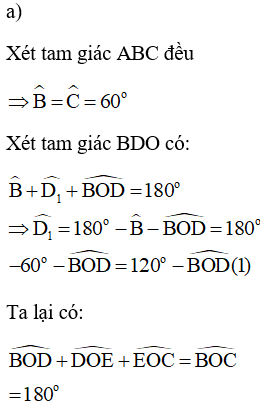
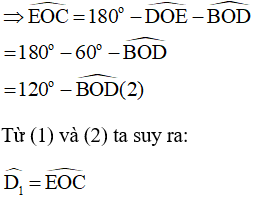
Từ (1) và (2) ta suy ra: $\widehat{D_1}=\widehat{EOC}$

Xét tam giác BOD và tam giác CEO có:

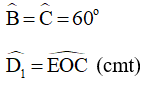
Do đó, tam giác BOD đồng dạng với tam giác CEO (góc – góc)

 $\Rightarrow \frac{BO}{CE}=\frac{BD}{CO}$$\Rightarrow BD.CE=BO.CO=\frac{B{C}^2}{4}$ (luôn không đổi)

b)

Ta có, tam giác BOD đồng dạng với tam giác CEO

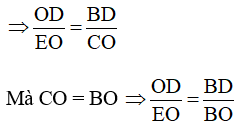
Xét tam giác BOD và tam giác OED có:

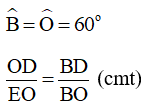
Do đó, tam giác BOD và tam giác OED  đồng dạng (cạnh – góc – cạnh)

$\Rightarrow \widehat{BDO}=\widehat{ODE}$

Do đó, DO là tia phân giác của $\widehat{BDE}$

c)

Gọi đường tròn tâm O tiếp xúc với AB có bán kính R.

Gọi H, K là chân đường vuông góc hạ từ O đến DE và AB

Do đó, R = OK

O thuộc đường phân giác DO của $\widehat{BDE}$

$\Rightarrow OH=OK=R$

Mà DE vuông góc với OH tại H

Do đó, DE tiếp xúc với (O; R) (đcpcm)

Bài 8 trang 134 SGK Toán lớp 9 tập 2: Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài (R > r). Hai tiếp tuyến chung AB và A’B’ của hai đường tròn (O), (O’) cắt nhau tại P (A và A’ thuộc đường tròn (O’), B và B’ thuộc đường tròn (O)). Biết PA = AB = 4 cm. Tính diện tích hình tròn (O’).

Lời giải:

(O; R) và (O’; R’) tiếp xúc ngoài với nhau

$\Rightarrow$OO’ = R + r.

Ta có:

O’A vuông góc với BP , OB vuông góc với BP

$\Rightarrow$O’A // OB

Do đó, tam giác PAO đồng dạng với tam giác PBO (định lý Ta–lét)

$\Rightarrow \frac{O‘A}{OB}=\frac{O‘P}{OP}$$=\frac{AP}{BP}=\frac{4}{8}=\frac{1}{2}$

$\Rightarrow OB=2O‘A\Rightarrow R=2r$ và $OP=2O‘P$$\Rightarrow O‘P=OO‘=R+r=3r$

Tam giác O’AP vuông tại A (do BP là tiếp tuyến của (O’) tại A)

Áp dụng định lý Py–ta–go ta có:

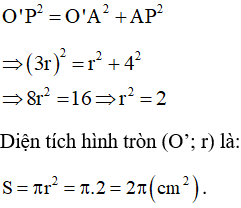
Bài 9 trang 135 SGK Toán lớp 9 tập 2: Cho tam giác ABC nội tiếp đường tròn (O’) và ngoại tiếp đường tròn (O). Tia AO cắt đường tròn (O’) tại D. Ta có:

(A) CD = BD = O’D;

(B) AO = CO = OF;

(C) CD = CO = BD;  

(D) CD = OD = BD.

Hãy chọn câu trả lời đúng.

Lời giải:

AB, AC tiếp xúc với đường tròn (O), AD đi qua O nên ta có:

$\widehat{CAD}=\widehat{BAD}=\alpha$ (tính chất giao nhau của hai tiếp tuyến)

AC, BC tiếp xúc với đường tròn (O) nên ta có:

$\widehat{ACO}=\widehat{BCO}=\beta$ (tính chất giao nhau của hai tiếp tuyến)

Xét đường tròn (O’)

Góc BAD là góc nội tiếp chắn cung nhỏ BD

Góc CAD là góc nội tiếp chắn cung nhỏ CD

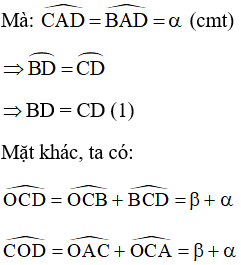
(góc ngoài của tam giác AOC)

Bài 10 trang 135 SGK Toán lớp 9 tập 2: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các cung nhỏ AB, BC, CA có số đo lần lượt là $x+{75}^o,2x+{35}^o,3x-{22}^o$. Một góc của tam giác ABC có số đo là:

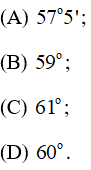
Hãy chọn câu trả lời đúng.

Lời giải:

Các cung AB, BC, CA tạo thành đường tròn, do đó:

Các góc của tam giác ABC là:

$\widehat{A}=\frac{1}{2}\left(2x+{25}^o\right)$$=\frac{1}{2}\left({2.47}^o+{25}^o\right)={59}^{o}30‘$ (tính chất góc nội tiếp chắn một cung)

$\widehat{B}=\frac{1}{2}\left(3x+{22}^o\right)$$=\frac{1}{2}\left({3.47}^o+{22}^o\right)={59}^{o}30‘$ (tính chất góc nội tiếp chắn một cung)

$\widehat{C}=\frac{1}{2}\left(x+{75}^o\right)$$=\frac{1}{2}\left({47}^o+{75}^o\right)={61}^o$ (tính chất góc nội tiếp chắn một cung)

Vậy ta chọn đáp án (C)

Bài 11 trang 135 SGK Toán lớp 9 tập 2: Từ một điểm P ở ngoài đường tròn (O), kẻ cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho: sđ$\stackrel{⏜}{BQ}={42}^o$ và sđ$\stackrel{⏜}{QD}={38}^o$. Tính tổng $\widehat{BPD}+\widehat{AQC}$.

Lời giải:

Góc BPD là góc có đỉnh nằm ngoài đường tròn chắn hai cung BD và AC

Góc AQC là góc nội tiếp chắn cung AC

Bài 12 trang 135 SGK Toán lớp 9 tập 2: Một hình vuông và một hình tròn có chu vi bằng nhau. Hỏi hình nào có diện tích lớn hơn ?

Lời giải:

Gọi cạnh hình vuông là a, bán kính đường tròn là R

Ta có: $4a=2\pi R\Rightarrow a=\frac{\pi R}{2}$

Lập tỉ số diện tích của hình vuông và hình tròn ta có: $\frac{S_{hv}}{S_{ht}}=\frac{a^2}{\pi R^2}=\frac{{\left(\frac{\pi R}{2}\right)}^2}{\pi R^2}=\frac{\pi }{4}<1$

Vậy hình tròn có diện tích lớn hơn hình vuông có cùng chu vi.

Bài 13 trang 135 SGK Toán lớp 9 tập 2: Cho đường tròn (O), cung BC có số đo bằng ${120}^0$, điểm A di chuyển trên cung lớn BC. Trên tia đối tia AB lấy điểm D sao cho AD = AC. Hỏi điểm D di chuyển trên đường nào?

Lời giải:

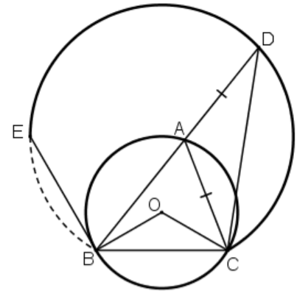
Ta có: Góc BAC là góc nội tiếp chắn cung BC

$\Rightarrow \widehat{BAC}=\frac{1}{2}sd\stackrel{⏜}{BC}$$=\frac{1}{2}{.120}^o={60}^o$

Mà $\widehat{DAC}+\widehat{BAC}={180}^o$ (hai góc kề bù)

$\Rightarrow \widehat{DAC}={180}^o-$$\widehat{BAC}={180}^o-{60}^o={120}^o$

Xét tam giác ADC có: AD = AC (cùng bằng bán kính đường tròn tâm A)

$\Rightarrow \widehat{D}=\widehat{ACD}=\frac{{180}^o-\widehat{CAD}}{2}$$=\frac{{180}^o-{120}^o}{2}={30}^o$

Hay $\widehat{BDC}={30}^o$ luôn không đổi. Do đó, D nằm trên cung chứa góc ${30}^o$ dựng trên đoạn BC. Khi A ≡ C thì D ≡ C, khi A ≡ B thì D ≡ E (BE là tiếp tuyến của đường tròn (O) tại B).

Vậy khi A di chuyển trên cung lớn BC thì D di chuyển trên cung CE thuộc cung chứa góc ${30}^o$ dựng trên BC.

Bài 14 trang 135 SGK Toán lớp 9 tập 2: Dựng tam giác ABC, biết BC = 4cm, $\widehat{A}={60}^o$, bán kính đường tròn nội tiếp tam giác bằng 1cm.

Lời giải:

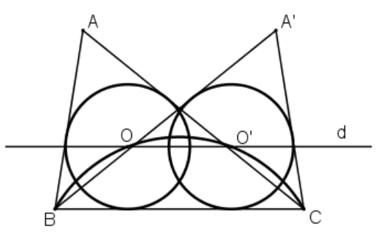
Cách dựng:

+ Dựng BC = 4cm

+ Dựng đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.

+ Dựng cung m chứa góc ${120}^0$ trên đoạn BC.

+ (d) cắt cung m tại O.

+ Dựng đường tròn tâm O, bán kính 1cm.

+ Kẻ tiếp tuyến từ B và C đến (O; 1cm).

Hai tiếp tuyến cắt nhau tại A. Có ΔABC là tam giác cần dựng.

Vì d cắt m tại hai điểm nên bài toán có hai nghiệm hình tam giác ABC và tam giác A’BC như hình vẽ.

Chứng minh:

Theo cách dựng có BC = 4cm . O thuộc cung ${120}^0$ dựng trên đoạn BC

$\Rightarrow \widehat{BOC}={120}^o$

A là giao của hai tiếp tuyến

Do đó, (O; 1cm) tiếp xúc với AB và AC

Mà khoảng cách từ O đến BC = 1cm.

Do đó, (O; 1cm) cũng tiếp xúc với BC

Do đó, (O; 1cm) là đường tròn nội tiếp tam giác ABC

Đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu

Bài 15 trang 135 SGK Toán lớp 9 tập 2: Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh:

a) $B{D}^2=AD.CD$;

b) Tứ giác BCDE là tứ giác nội tiếp;

c) BC song song với DE.

Lời giải:

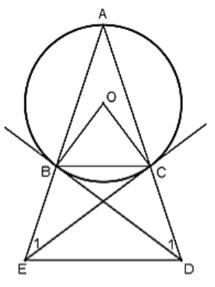
a)

Góc BAC là góc nội tiếp chắn cung BC

Góc CBD là góc tạo bởi tia tiếp tuyến BD và dây cung BC

$\Rightarrow \widehat{BAC}=\widehat{CBD}=\frac{1}{2}sd\stackrel{⏜}{BC}$

Xét tam giác ABD và tam giác BCD có:

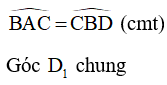
Do đó, tam giác ABD và tam giác BCD đồng dạng (góc – góc)

$\Rightarrow \frac{BD}{CD}=\frac{AD}{BD}\Rightarrow B{D}^2=AD.CD$

b)

Tam giác ABC cân tại A nên ta có: AB = AC $\Rightarrow \stackrel{⏜}{AB}=\stackrel{⏜}{AC}$

Góc $D_1$ là góc có đỉnh bên ngoài đường tròn chắn cung AB và cung BC nên ta có:

$\widehat{E_1}=\frac{1}{2}\left(sd\stackrel{⏜}{AC}-sd\stackrel{⏜}{BC}\right)$

Do đó, góc D và góc E cùng nhìn BC dưới 1 góc bằng nhau

Do đó, BCDE là tứ giác nội tiếp

c)

BCDE là tứ giác nội tiếp (cmt)

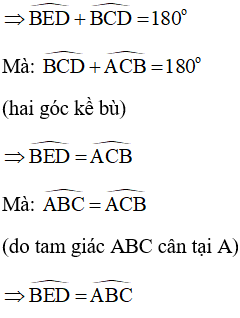
Mà góc BED và góc ABC là hai góc đồng vị, do đó, BC // DE.

Bài 16 trang 135 SGK Toán lớp 9 tập 2: Một mặt phẳng chứa trụ OO’ của một hình trụ; phần mặt phẳng nằm trong hình trụ là một hình chữ nhật có chiều dài 3cm, chiều rộng 2cm.Tính diện tích xung quanh và thể tích hình trụ đó.

Lời giải:

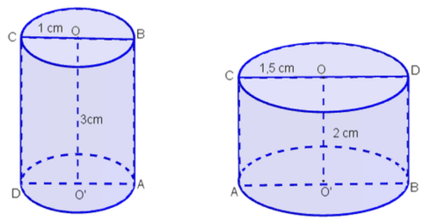
Xét hai trường hợp

TH1: Đường cao hình trụ là h = 3cm, đường kính đáy trụ bằng 2cm

Bán kính đáy của hình trụ là: R = 2 : 2 = 1 (cm)

Diện tích xung quanh hình trụ là: $S_{xq}=2\pi Rh$$=2\pi \mathrm{.1.3}=6\pi \left(c{m}^2\right)$

Thể tích hình trụ là: $V=\pi R^{2}h=\pi {.1}^2.3=3\pi \left(c{m}^3\right)$

TH2: Đường cao hình trụ là h = 2cm, đường kính đáy trụ bằng 3cm

Bán kính đáy của hình trụ là: R = 3 : 2 = 1,5 (cm)

Diện tích xung quanh hình trụ là: $S_{xq}=2\pi Rh=2\pi .1,5.2$$=6\pi \left(c{m}^2\right)$

Thể tích hình trụ là: $V=\pi R^{2}h=\pi .1,5^2.2$$=4,5\pi \left(c{m}^3\right)$.

Bài 17 trang 135 SGK Toán lớp 9 tập 2: Khi quay tam giác ABC vuông ở A một vòng quanh cạnh góc vuông AC cố định, ta được một hình nón. Biết rằng BC = 4dm, $\widehat{ACB}={30}^o$. Tính diện tích xung quanh và thể tích hình nón.

Lời giải:

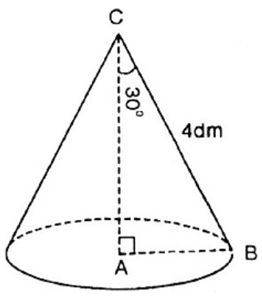
Xét tam giác ABC vuông tại A có:

$AB=BC.\sin C=BC.\sin {30}^o=4.\frac{1}{2}=2 \left(dm\right)$

$AC=BC.cosC=BC.cos{30}^o=4.\frac{\sqrt{3}}{2}=2\sqrt{3} \left(dm\right)$

Diện tích xung quanh hình nón là:

$S_{xq}=\pi AB.BC=\pi \mathrm{.2.4}=8\pi \left(d{m}^2\right)$

Thể tích hình nón là: 

$V=\frac{1}{3}\pi .A{B}^2.AC=\frac{1}{3}\pi {.2}^2.2\sqrt{3}=\frac{8}{\sqrt{3}}\pi \left(d{m}^3\right)$

Bài 18 trang 135 SGK Toán lớp 9 tập 2: Một hình cầu có số đo diện tích (đơn vị: $m^2$) bằng số đo thể tích (đơn vị: $m^3$). Tính bán kính hình cầu, diện tích mặt cầu và thể tích hình cầu.

Lời giải:

Gọi bán kính của hình cầu là R

Vậy diện tích mặt cầu và thể tích khối cầu có bán kính R = 3m là: $S=4\pi R^2=4\pi {.3}^2=36\pi \left(m^2\right)$