50 Bài tập Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích của hình nón, hình nón cụt (có đáp án)- Toán 9

Bài tập Toán 9 Chương 4 Bài 2: Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích của hình nón, hình nón cụt

A. Bài tập Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích của hình nón, hình nón cụt

I. Bài tập trắc nghiệm

Câu 1: Cho hình nón có bán kính đáy R = 3(cm) và chiều cao h = 4(cm). Diện tích xung quanh của hình nón là:

A. 25π (cm2)

B. 12π (cm2)

C. 20π (cm2)

D. 15π (cm2)

Lời giải:

Chọn đáp án D.

Câu 2: Cho hình nón có đường kính đáy d = 10 cm và diện tích xung quanh 65π (cm2) . Tính thể tích khối nón:

A. 100π (cm3)

B. 120π (cm3)

C. 300π (cm3)

D. 200π (cm3)

Lời giải:

Chọn đáp án A.

Câu 3: Cho hình nón có chiều cao h = 10cm và thể tích V = 1000π (cm3). Tính diện tích toàn phần của hình nón:

Lời giải:

Ta có:

Chọn đáp án B.

Câu 4: Một chiếc xô hình nón cụt làm bằng tôn để đựng nước. Các bán kính đáy là 10cm và 5cm, chiều cao là 20cm. Tính dung tích của xô:

Lời giải:

Ta có:

Chọn đáp án A.

Câu 5: Cho tam giác ABC vuông tại A có: BC = 20cm; AC = 12cm. Quay tam giác ABC cạnh AB ta được một hình nón có thể tích là:

A. 2304π (cm3)

B. 1024π (cm3)

C. 786π (cm3)

D. 768π (cm3)

Lời giải:

Chọn đáp án D.

Câu 6: Cho một hình nón có bán kính đáy r = 5cm và đường sinh 13cm. Tính thể tích hình nón

A. 100π

B. 30π

C. 300π

D. 325π

Lời giải:

Ta có:

Chọn đáp án A.

Câu 7: Cho hình nón có thể tích 100π và chu vi đáy là 10π. Tính độ dài đường sinh

A. 12

B. 20

C.13

D. 14

Lời giải:

Chọn đáp án C.

Câu 8: Cho hình nón có bán kính đáy là r = 10 cm và đường sinh dài 26 cm. Tính chiều cao của hình nón

A. 12 cm

B. 24 cm

C. 20 cm

D. 16cm

Lời giải:

Ta có:

Chọn đáp án B.

Câu 9: Cho hình nón có diện tích đáy là 9π cm2, đường sinh 5cm. Tính chiều cao của hình nón?

A. 3cm

B.5cm

C. 7cm

D. 4cm

Lời giải:

Chọn đáp án D.

Câu 10: Một hình nón có đường sinh gấp 2 lần bán kính đường tròn đáy. Tìm khẳng định đúng?

A. h = √3r

B. h = 2r C .h = r

D. h = √2r

Lời giải:

Ta có:

Chọn đáp án A.

Câu 11: Cho hình thang vuông ABDC vuông tại A và B, biết cạnh AB = BC = 3m, AD = 5m. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh AB

Lời giải:

Kẻ CH ⊥ BD tại H. Khi đó ACHB là hình vuông nên

CH = AB = AC = BH = 3cm ⇒ HD = 4 – 3 = 1cm

Xét tam giác vuông CHD ta có CD2 = CH2 + HD2 = 32 + 12 = 10 ⇒ CD = √10 

Khi quay hình thang vuông ABDC quanh cạnh AB ta được hình nón cụt có bán kính đáy nhỏ AC, bán kính đáy lớn BD, đường sinh CD và chiều cao AB

Khi đó diện tích xung quanh hình nón cụt là

Đáp án cần chọn là: B

Câu 12: Cho hình thang vuông ABCD vuông tại A và B, biết cạnh AB = BC = 4,5 cm, AD = 7,5cm. Tính diện tích xung quanh hình nón cụt tạo thành khi quay hình thang quanh cạnh AB

Lời giải:

Kẻ CH ⊥ BD tại H. Khi đó ACHB là hình vuông nên

CH = AB = AC = BH = 4,5cm ⇒ HD = 6 – 4,5 = 1,5cm

Xét tam giác vuông CHD ta có CD2 = CH2 + HD2 = 4,52 + 1,52 = 22,5

Khi quay hình thang vuông ABDC quanh cạnh AB ta được hình nón cụt có bán kính đáy nhỏ AC, bán kính đáy lớn BD, đường sinh CD và chiều cao AB

Khi đó diện tích xung quanh hình nón cụt là

Đáp án cần chọn là: C

Câu 13: Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên hai lần thì diện tích xung quanh của hình nón đó

A. Tăng 4 lần                                    

B. Giảm 4 lần

C. Tăng 2 lần                                    

D. Không đổi

Lời giải:

Ta có đường sinh mới l’2 = (2R)2 + (2h)2 = 4 (R2 + h2) = (2l)2 ⇒ l’ = 2l

Khi đó diện tích xung quanh mới S’xq =  (2R). (2l) = 4. Rl = 4Sxq

Vậy diện tích xung quanh của hình nón tăng 4 lần

Đáp án cần chọn là: A

Câu 14: Nếu ta tăng bán kính đáy và chiều cao của một hình nón lên ba lần thì diện tích xung quanh của hình nón đó

A. Tăng 3 lần                                    

B. Giảm 3 lần

C. Tăng 9 lần                                    

D. Không đổi

Lời giải:

Ta có đường sinh mới l’2 = (3R)2 + (3h)2 = 9(R2 + h2) = (3l)2 ⇒ l’ = 3l

Khi đó diện tích xung quanh mới S’xq =  (3R). (3l) = 9. Rl = 9Sxq

Vậy diện tích xung quanh của hình nón tăng 9 lần

Đáp án cần chọn là: C

Câu 15: Cho tam giác ABC đều cạnh a, đường trung tuyến AM. Quay tam giác ABC quanh cạnh AM. Tính diện tích toàn phần của hình nón tạo thành

Lời giải:

Xét tam giác ABC đều có AM vừa là đường trung tuyến, đường cao, đường phân giác nên ta có 

Khi quay tam giác ABC quanh cạnh AM ta được hình nón đỉnh A, bán kính đáy là MC, đường sinh AC và chiều cao AM

Diện tích toàn phần của hình nón là:

Đáp án cần chọn là: B

II. Bài tập tự luận có lời giải

Câu 1: Một hình nón có bán kính đáy bằng và diện tích xung quanh là . Tính thể tích của hình nón đó.

Lời giải:

Ta có Sxq = πRl. Theo giả thiết ta có: Sxq = 65π (cm2) ⇒ πRl = 65π (cm2)

Khi đó ta có:

III. Bài tập vận dụng

Câu 1: Cho hình nón như hình bên:

Biết rằng đáy là hình tròn có bán kính bằng 3cm, đường sinh có độ dài là 5cm. Hãy tính diện tích xung quanh, diện tích toàn phần và thể tích của hình nón đó.

Câu 2: Cho hình nón cụt như hình vẽ

Biết rằng bán kính của đáy nhỏ là r = 3cm, bán kính của đáy lớn là R = 6cm, độ dài AB = 4cm. Hãy tính diện tích xung quanh và thể tích của hình nón cụt

B. Lý thuyết Hình nón – Hình nón cụt – Diện tích xung quanh và thể tích của hình nón, hình nón cụt

1. Hình nón

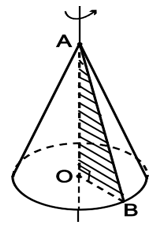
Khi quay tam giác vuông AOC một vòng quanh cạnh OA cố định thì được một hình nón.

– Điểm A được gọi đỉnh của hình nón.

– Hình tròn (O) được gọi là đáy của hình nón.

– Mỗi vị trí của AC được gọi là một đường sinh của hình nón.

– Đoạn AO được gọi là đường cao của hình nón.

2. Diện tích và thể tích của hình nón

Đặt AC = l; l là đường sinh.

Cho hình nón có bán kính đáy R và đường sinh l, chiều cao h.

– Diện tích xung quanh: S_xq = πRl.

– Diện tích toàn phần: S_tp = πRl + πR².

– Thể tích: $V=\frac{1}{3}\pi R^{2}h$.

Ví dụ 1. Một hình nón có đường cao bằng 24 cm và thể tích bằng 800π cm3. Tính diện tích toàn phần của hình nón này.

Lời giải:

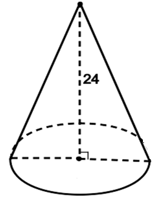
Gọi R là bán kính và h là chiều cao của hình nón.

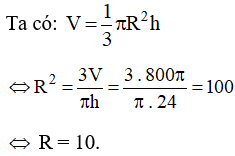
Do đó bán kính của hình nón là 10 cm.

Đường sinh của hình nón là:

$S{B}^2=\sqrt{S{O}^2+O{B}^2}$$=\sqrt{{24}^2+{10}^2}=26\left(cm\right)$

Diện tích toàn phần của hình nón là:

Stp = πR(l + R) = π . 10 (26 + 10) = 360π (cm²).

3. Hình nón cụt

Khi cắt hình nón bởi một mặt phẳng song song với đáy thì phần hình nón nằm giữa mặt phẳng nói trên và mặt phẳng đáy được gọi là một hình nón cụt.

– Hai hình tròn (O) và (O’) được gọi là hai đáy.

– Đoạn OO’ được gọi là trục. Độ dài OO’ là chiều cao.

– Đoạn AC được gọi là đường sinh.

4. Diện tích và thể tích hình nón cụt

Cho hình nón cụt có các bán kính đáy R và r, chiều cao h, đường sinh l.

– Diện tích xung quanh: S_xq = π (R + r) l.

– Thể tích: $V=\frac{1}{3}\pi h(R^2+Rr+r^2)$.

Ví dụ 2. Một hình nón đỉnh S có bán kính đáy bằng 9 cm và chiều cao SO = 21,6 cm. Cắt hình nón bởi một mặt phẳng song song với đáy tạo ra một hình nón cụt có chiều cao 12 cm. Tính diện tích xung quanh của hình nón cụt.

Lời giải:

Xét mặt cắt qua trục của hình nón là ∆SAB cân tại S.

Trong mặt phẳng SAB có O’C // OB.

Theo định lý Ta – lét ta có $\frac{O‘C}{OB}=\frac{SO‘}{SO}$.

Do đó $\frac{O‘C}{9}=\frac{9,6}{21,6}\Rightarrow$ O’C = 4 (cm).

Trong mặt phẳng SAB vẽ $CH\perp AB$, ta được:

CH = OO’ = 12 cm, BH = 9 – 4 = 5 (cm).

Suy ra BC = $\sqrt{B{H}^2+C{H}^2}$$=\sqrt{{12}^2+5^2}=13$ (cm)

Diện tích xung quanh của hình nón cụt là:

Sxq = π(R₁ + R₂)l = π(9 + 4) . 13 = 169π (cm²)

Vậy diện tích xung quanh của hình nón cụt là 169π cm².

Xem thêm