Lý thuyết Toán lớp 8 Bài 6: Hình thoi
A. Lý thuyết Hình thoi
1. Khái niệm
Hình thoi là tứ giác có bốn cạnh bằng nhau.
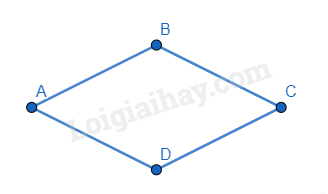
2. Tính chất
– Các cạnh đối song song
– Các góc đối bằng nhau
– Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
– Hai đường chéo là các đường phân giác của các góc ở đỉnh.
Dấu hiệu nhận biết hình thoi
– Hình bình hành có hai cạnh kề bằng nhau là hình thoi.
– Hình bình hành có hai đường chéo vuông góc với nhau là hình thoi.
– Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi.
Ví dụ:
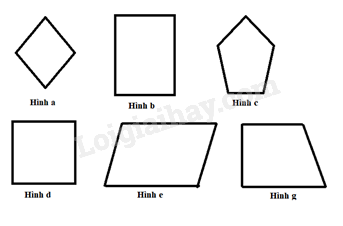
Hình a, d là hình thoi.

B. Bài tập Hình thoi
Bài 1. Cho hình thoi có độ dài hai đường chéo là 24 cm và 10 cm. Tính độ dài cạnh hình thoi.
Hướng dẫn giải
Giả sử hình thoi có hai đường chéo cắt nhau tại H và AC = 10 cm, BD = 24 cm.
Do ABCD là hình thoi nên:
AC ⊥ BD
Xét tam giác AHB vuông tại H:
AB2 = AH2 + HB2 = 52 + 122 = 169
Do đó AB = 13 cm.
Bài 2. Cho tam giác ABC vuông ở A, trung tuyến AM. Gọi D là trung điểm của AB, M’ là điểm đối xứng với M qua D. Tứ giác AMBM’ là hình gì?
Hướng dẫn giải
Vì M’ đối xứng M qua D nên DM = DM’
M là trung điểm BC
D là trung điểm AB
Suy ra MD là đường trung bình của ΔABC.
Suy ra MD // AC.
Mặt khác ΔABC vuông ở A nên AB ⊥ AC.
Do đó AB ⊥ DM hay AB ⊥ MM’.
Vì D là trung điểm của AB và MM’ nên tứ giác AMBM’ là hình bình hành.
Mà AB ⊥ MM’ nên AMBM’ là hình thoi.
Vậy AMBM’ là hình thoi.
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 2: Tứ giác
Lý thuyết Bài 3: Hình thang cân
Lý thuyết Bài 4: Hình bình hành
Lý thuyết Bài 5: Hình chữ nhật
Lý thuyết Bài 6: Hình thoi
Lý thuyết Bài 7: Hình vuông