Lý thuyết Toán lớp 8 Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều
A. Lý thuyết Hình chóp tam giác đều – Hình chóp tứ giác đều
1. Hình chóp tam giác đều
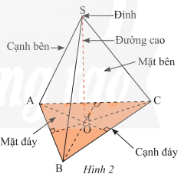
Hình chóp tam giác đều có:
– Đáy là tam giác đều.
– 3 cạnh bên bằng nhau.
– 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
– 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.
– Chân đường cao trùng với tâm của đáy.
2. Hình chóp tứ giác đều

Hình chóp tứ giác đều có:
– Đáy là hình vuông.
– 4 cạnh bên bằng nhau.
– 4 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.
– 4 cạnh đáy bằng nhau là bốn cạnh của hình vuông đáy.
– Chân đường cao trùng với giao điểm của hai đường chéo của mặt đáy.

B. Bài tập Hình chóp tam giác đều – Hình chóp tứ giác đều
Bài 1.Phát biểu sau đúng hay sai? Nếu sai hãy sửa lại để có phát biểu đúng.
a) Hình chóp tam giác đều có các mặt bên và mặt đáy là các tam giác cân.
b) Hình chóp tam giác đều có 3 mặt bên là các tam giác cân.
c) Hình chóp tứ giác đều có đáy là hình chữ nhật.
d) Hình chóp tứ giác đều có 1 đỉnh, 4 mặt bên và 1 mặt đáy.
Hướng dẫn giải
|
Phát biểu |
Đúng/ Sai |
Sửa lại để có phát biểu đúng (Đối với phát biểu sai) |
|
a) Hình chóp tam giác đều có các mặt bên và mặt đáy là các tam giác cân. |
Sai |
Hình chóp tam giác đều có mặt đáy là tam giác đều và các mặt bên là các tam giác cân. |
|
b) Hình chóp tam giác đều có 3 mặt bên là các tam giác cân. |
Đúng |
|
|
c) Hình chóp tứ giác đều có đáy là hình chữ nhật. |
Sai |
Hình chóp tứ giác đều có đáy là hình vuông. |
|
d) Hình chóp tứ giác đều có 1 đỉnh, 4 mặt bên và 1 mặt đáy. |
Đúng |
Bài 2.Cho hình chóp tam giác đều S.ABC có cạnh bên SC = 9 cm, cạnh đáy AB = 4 cm. Hãy cho biết:
a) Mặt bên và đỉnh của hình chóp.
b) Độ dài các cạnh bên và cạnh đáy còn lại của hình chóp.
c) Số đo mỗi góc của mặt đáy.
Hướng dẫn giải
a) Hình chóp tam giác đều S.ABC có 3 mặt bên là SAB, SAC, SBC và đỉnh S.
b) Vì ba mặt bên SAB, SBC, SCA là các tam giác cân bằng nhau nên SA = SB = SC
Mà SC = 9 cm, suy ra SA = SB = 9 cm.
Vì mặt đáy ABC là tam giác đều nên AB = BC = CA
Mà AB = 4 cm, suy ra BC = AC = 4 cm.
c) Vì mặt đáy ABC là tam giác đều nên
Bài 3.Cho hình chóp tứ giác đều O.DEGH có cạnh bên OD = 10 cm và cạnh đáy DE = 7 cm. Hãy cho biết:
a) Mặt bên, mặt đáy và đường cao của hình đó. Mặt đáy và các mặt bên của hình chóp là hình gì?
b) Độ dài các cạnh bên và cạnh đáy còn lại của hình đó
c) Số đo mỗi góc của mặt đáy.
Hướng dẫn giải
a) Hình chóp tứ giác đều O.DEGH có 4 mặt bên là ODE, OEG, OGH, OHD; mặt đáy là DEGH.
Gọi I là giao điểm của hai đường chéo của mặt đáy.
Khi đó OI là đường cao của hình chóp tứ giác đều O.DEGH.
b) Vì bốn mặt bên ODE, OEG, OGH, OHD là các tam giác cân bằng nhau nên OD = OE = OG = OH.
Mà OD = 10 cm, suy ra OE = OG = OH = 10 cm.
Vì mặt đáy DEGH là hình vuông nên DE = EG = GH = HD
Mà DE = 7 cm, suy ra EG = GH = HD = 7 cm.
c) Vì mặt đáy DEGH là hình vuông nên
Bài 4.Trong các tấm bìa dưới đây, tấm bìa nào gấp được thành hình chóp tứ giác đều, hình chóp tam giác đều?
Hướng dẫn giải
Hình chóp tam giác đều có tất cả các mặt đều là tam giác, bao gồm 1 mặt đáy là tam giác đều và 3 mặt bên là tam giác cân.
Hình chóp tứ giác đều có 5 mặt, bao gồm 1 mặt đáy là hình vuông và 4 mặt bên là tam giác cân.
Khi đó tấm bìa hình b và hình c không gấp được hình chóp tam giác đều và hình chóp tứ giác đều.
Hình a) khi gấp lại thì được một hình chóp tứ giác đều.
Hình d) có 4 mặt đều là tam giác đều, tuy nhiên không gấp được hình chóp tam giác đều.
Video bài giảng Toán 8 Hình chóp tam giác đều – Hình chóp tứ giác đều – Chân trời sáng tạo
Xem thêm các bài tóm tắt Lý thuyết Toán lớp 8 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 7: Nhân, chia phân thức
Lý thuyết Bài 1: Hình chóp tam giác đều – Hình chóp tứ giác đều
Lý thuyết Bài 2: Diện tích xung quanh và thể tích của hình chóp tam giác đều, hình chóp tứ giác đều
Lý thuyết Bài 1: Định lí Pythagore
Lý thuyết Bài 2: Tứ giác
Lý thuyết Bài 3: Hình thang – Hình thang cân