50 Bài tập Tính chất cơ bản của phân thức đại số (có đáp án)- Toán 8

Bài tập Toán 8 Chương 2 Bài 2: Tính chất cơ bản của phân thức

A. Bài tập Tính chất cơ bản của phân thức.

I. Bài tập trắc nghiệm

Bài 1: Cho phân thức $\frac{2}{\left(x–1\right)}$, nhân cả tử và mẫu với đa thức (x + 1) ta được phân thức mới là ?

Nhân cả tử và mẫu với đa thức (x + 1) ta được phân thức mới là

Ta có

(áp dụng hằng đẳng thức A² – B² = ( A – B )( A + B ) )

Chọn đáp án C.

Bài 2: Với giá trị nào của x thì hai phân thức $\frac{(x – 2)}{(x^2 – 5x + 6)}$ và $\frac{1}{\left(x–3\right)}$ bằng nhau ?

A. x = 2   

B. x = 3

C. x ≠ 2, x ≠ 3.   

D. x = 0.

Lời giải:

+ Giá trị của phân thức $\frac{\left(x–2\right)}{\left(x^2–5x+6\right)}$ được xác định khi và chỉ khi x² – 5x + 6 ≠ 0

⇔ ( x – 3 )( x – 2 ) ≠ 0 hay x ≠ 2,x ≠ 3.

+ Giá trị của phân thức $\frac{1}{\left(x–3\right)}$ được xác định khi và chỉ khi x – 3 ≠ 0 hay x ≠ 3.

Với x ≠ 2,x ≠ 3 ta có:

Vậy với x ≠ 2,x ≠ 3 ta có: $\frac{\left(x–2\right)}{\left(x^2–5x+6\right)}$ = $\frac{1}{\left(x–3\right)}$

Chọn đáp án C.

Bài 3: Phân thức $\frac{2}{\left(x+3\right)}$ bằng với phân thức nào dưới đây ?

Lời giải:

+

⇒ Đáp án A sai.

+

⇒ Đáp án B sai.

+

⇒ Đáp án C đúng.

+

⇒ Đáp án D sai.

Chọn đáp án C.

Bài 4: Điền vào chỗ trống đa thức sao cho:

   A. x² – 4x.

   B. x² + 4x.

   C. x² + 4.

   D. x² – 4.

Lời giải:

Gọi A là đa thức cần tìm thỏa mãn A( x – 4 ) = x( $x^2$ – 16 )

Ta có: A( x – 4 ) = x( x – 4 )( x + 4 ) ⇒ A = x( x + 4 ) = $x^2$ + 4x

Chọn đáp án B.

Bài 5: Dùng quy tắc đổi dấu, hãy điền đa thức thích hợp vào chỗ trống để được đẳng thức:

   A. 2y- x     B. x – 2y

   C. 2y + x     D. – 2y – x

Áp dụng quy tắc đổi dấu ta có:

Vậy đa thức cần điền là x – 2y

Chọn đáp án B

Bài 6: Áp dụng tính chất cơ bản của phân số, điền đa thức thích hợp vào chỗ trống

A. 2y(x – y)    

B. y(x + y)

C. 2x(x + y)    

D. 2y (x + y)

Lời giải:

Ta có:

Vậy đa thức cần điền vào chỗ trống là 2y(x+ y)

Chọn đáp án D

Bài 7: Điền đa thức thích hợp vào chỗ trống sau:

 A. 5xy    

B.5x

C. 5y   

D. 5x²y

Lời giải:

Ta có:

Vậy đa thức cần điền là: 5xy

Chọn đáp án A

Bài 8: Điền đa thức thích hợp vào chỗ trống sau:

A. 10x – 10y    

B. 10 – 10x

C. 10.(1 – xy)   

D. Đáp án khác

Lời giải:

Ta có:

Vậy đa thức cần điềm vào chỗ chấm là: 10(1 – xy )

Chọn đáp án C

Bài 9: Tìm a biết:

A. a = 2    

B. a = 1

C. a = 4    

D. a = – 2

Lời giải:

Mà  nên a = 2

Chọn đáp án A

Bài 10: Dùng quy tắc đổi dấu, điền đa thức thích hợp vào chỗ trống

A. x – 1    

B. xy – 1

C. x(y – 1)    

D. x(x – 1)

Lời giải:

Chọn đáp án D

II. Bài tập tự luận

Bài 1: Cho A = . Có bao nhiêu giá trị của x để A = 0?

Lời giải

Ta có

x⁴ – 10x² + 9 = x⁴ – x² – 9x² + 9 = x²(x² – 1) – 9(x² – 1) = (x² – 1)(x² – 9)

Vậy có hai giá trị của x thỏa mãn đề bài x = 2; x = -2.

Bài 2: Cho B = . Có bao nhiêu giá trị của x để B = 0.

Lời giải

Ta có: x⁴ – 4x² = x²(x – 4) = x²(x – 2)(x + 2)

Điều kiện:

Vậy có bốn giá trị của x thỏa mãn đề bài x = 4; x = -4; x = 1; x = -1.

Bài 3: Với x ≠ y, hãy viết phân thức  dưới dạng phân thức có tử là x² – y²?

Lời giải

Ta có:

Bài 4: Với x ≠ y, hãy viết phân thức  dưới dạng phân thức có mẫu là x⁵y²(x – y)?

Lời giải

Nhân cả tử và mẫu của phân thức  với x⁴y²(x – y) ta được:

Ta có:

Bài 5: Dùng tính chất cơ bản của phân thức, hãy tìm đa thức C biết ?

Lời giải

Vậy C = x(x + 2).

Bài 6: Hãy dùng tính chất cơ bản của phân thức để điền một đa thức thích hợp vào chỗ trống

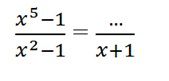
Lời giải:

Vế phải là kết quả phép chia tử của vế trái x⁵ – 1 cho x – 1.

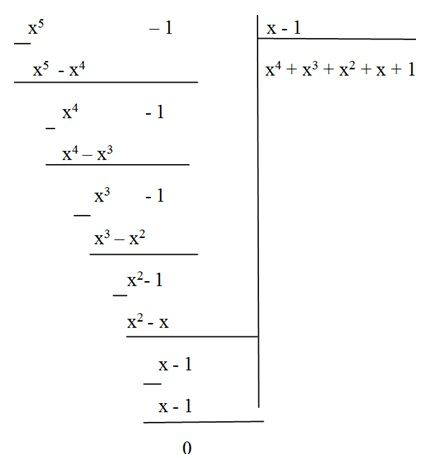
Vậy phải điền x⁴ + x³ + x² + x + 1 vào chỗ trống.

Bài 7

Cho phân thức $\frac{x}{3}$. Hãy nhân cả tử và mẫu của phân thức này với x + 2 rồi so sánh phân thức vừa nhận được với phân thức đã cho.

Lời giải

Nhân tử số: x.(x + 2) = x² + 2x

Nhân mẫu số: 3.(x +2) = 3x + 6

⇒ x(3x + 6) = 3(x² + 2x) = 3x² + 6x

Vậy :

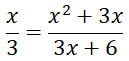
Bài 8: Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết:

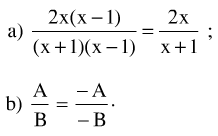
Lời giải:

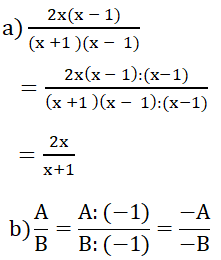
Bài 9

Hãy nhắc lại tính chất cơ bản của phân số.

Lời giải

– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì được một phân số bằng phân số đã cho.

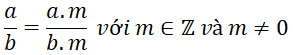
– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì được một phân số bằng phân số đã cho.

Bài 10: Trong tờ nháp của một bạn có ghi các phép rút gọn phân thức như hình sau:

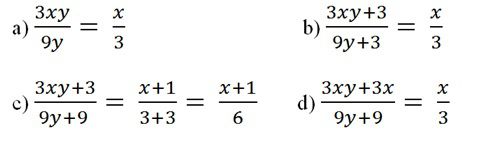
Theo em câu nào đúng, câu nào sai? giải thích.

Lời giải:

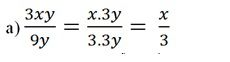
Đúng vì rút gọn sau khi đã chia cả tử và mẫu của vế trái cho 3y.

b) Vế phải chứng tỏ đã chia mẫu ở vế trái cho 3y + 1 vì 9y + 3 = 3(3y + 1).

Nhưng tử của của vế trái không có nhân tử 3y + 1. Vì vậy phép rút gọn này sai.

c) Sai, vì y không phải là nhân tử chung của tử và mẫu của vế trái.

d) Đúng, vì đã rút gọn phân thức ở vế trái với nhân tử chung là 3(y + 1).

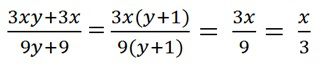
III. Bài tập vận dụng

Bài 1: Viết các thương sau dưới dạng phân thức:

a) 5 : (x + 3)                  b) (a + 25) : 7

Bài 2: Cho phân thức $\frac{x}{3}$.

Hãy nhân tử và mẫu của phân thức này với x + 2.

Xét xem hai phân thức $\frac{x}{3}$ và $\frac{x(x+2)}{3(x+2)}$ có bằng nhau không?

Bài 3: Cho phân thức $\frac{3x^{2}y}{6x{y}^3}$

Hãy chia cả tử và mẫu phân thức này cho 3xy;

Xét xem hai phân thức và có bằng nhau không?

Bài 4: Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao: 

$\frac{2x(x-1)}{(x+1)(x-1)}=\frac{2x}{x+1}$;       $\frac{A}{B}=\frac{-A}{-B}$

Bài 5: Dùng quy tắc đổi dấu hãy điền một đa thức thích hợp vào chỗ trống (….) trong mỗi đẳng thức sau:

$\frac{3}{x-5}=\frac{...}{5-x}$;      $\frac{x-1}{5x}=\frac{1-x}{...}$

Bài 6: Dùng tính chất cơ bản của phân thức, hãy điền đa thức thích hợp vào chỗ trống (…) trong mỗi đẳng thức sau:

a) $\frac{x-x^2}{5x^2-5}$=$\frac{x}{Q}$

b) $\frac{Q}{x-y}$=$\frac{3x^2-3xy}{3(y-x{)}^2}$

Bài 7: Hãy viết phân thức $\frac{3}{x-2}$ dưới dạng phân thức có mẫu số lần lượt là:

a) $x^2-2x$         b) $x^2-4$         

c) $6-3x$              d)$(x-2{)}^2$

Bài 8: Dùng tính chất cơ bản của phân thức, hãy viết mỗi phân thức sau dưới dạng phân thức có mẫu số là $12x^{2}y$:

a) $\frac{1}{6x^2}$     b) $\frac{5}{3xy}$   

c) $\frac{7x}{4y}$         d) $\frac{5}{12x}$

Bài 9: Hãy biểu diễn đa thức $3x-y$ dưới dạng phân thức có mẫu số lần lượt là:

a) 7                      b) x               

c) $9x+y$            d) $3x-y$

Bài 10: Hãy viết phân thức $\frac{3}{x-2}$ dưới dạng phân thức có mẫu số lần lượt là:

a) $x^2-2x$         b) $x^2-4$         

c) $6-3x$              d)$(x-2{)}^2$

B.Lý thuyết Tính chất cơ bản của phân thức

1. Tính chất cơ bản của phân thức

+ Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

 (M là một đa thức khác đa thức 0)

+ Nếu chia cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

 (M là một đa thức khác đa thức 0)

Ví dụ: Cho phân thức (2x)/(x + 2). Nhân cả tử và mẫu với đa thức ( x – 1 ), so sánh phân thức nhận được với phân thức đã cho ?

Hướng dẫn:

Ta có phân thức mới là 

Ta có  = (2x)/(x + 2) vì 2x( x – 1 ).( x + 2 ) = 2x.( x + 2 )( x – 1 ).

2. Quy tắc đổi dấu

Nếu đổi dấu cả tử và mẫu của một phân thức thì nhận được phân thức mới bằng phân thức đã cho.

Ta có thể viết như sau: 

Ví dụ: Ta có phân thức . Đổi dấu cả tử và mẫu ta được phân thức mới, so sánh phân thức mới với phân thức đã cho

Hướng dẫn:

Ta có phân thức mới nhận được là.

Ta có: = vì x. – ( x + 1 ) = – x.( x + 1 ).

Xem thêm