50 Bài tập Phương trình tích (có đáp án)- Toán 8

Bài tập Toán 8 Chương 3 Bài 4: Phương trình tích

A. Bài tập Phương trình tích

I. Bài tập trắc nghiệm

Bài 1: Nghiệm của phương trình ( x + 2 )( x – 3 ) = 0 là?

   A. x = – 2.   B. x = 3.

   C. x = – 2; x = 3.   D. x = 2.

Lời giải:

Ta có: ( x + 2 )( x – 3 ) = 0 ⇔ 

Vậy nghiệm của phương trình là x = – 2; x = 3.

Chọn đáp án C.

Bài 2: Tập nghiệm của phương trình ( 2x + 1 )( 2 – 3x ) = 0 là?

   A. S = { – $\frac{1}{2}$ }.   B. S = { – $\frac{1}{2}$; $\frac{3}{2}$ }

   C. S = { – $\frac{1}{2}$; $\frac{2}{3}$ }.   D. S = { $\frac{3}{2}$ }.

Lời giải:

Ta có: ( 2x + 1 )( 2 – 3x ) = 0 ⇔ 

Vậy tập nghiệm của phương trình S = { – $\frac{1}{2}$; $\frac{2}{3}$ }.

Chọn đáp án C.

Bài 3: Nghiệm của phương trình 2x( x + 1 ) = x² – 1 là?

A. x = – 1.   

B. x = ± 1.

C. x = 1.   

D. x = 0.

Lời giải:

Ta có: 2x( x + 1 ) = x² – 1 ⇔ 2x( x + 1 ) = ( x + 1 )( x – 1 )

⇔ ( x + 1 )( 2x – x + 1 ) = 0 ⇔ ( x + 1 )( x + 1 ) = 0

⇔ ( x + 1 )2 = 0 ⇔ x + 1 = 0 ⇔ x = – 1.

Vậy phương trình có nghiệm là x = – 1.

Chọn đáp án A.

Bài 4: Giá trị của m để phương trình ( x + 2 )( x – m ) = 4 có nghiệm x = 2 là?

A. m = 1.   

B. m = ± 1.

C. m = 0.   

D. m = 2.

Lời giải:

Phương trình ( x + 2 )( x – m ) = 4 có nghiệm x = 2, thay x = 2 vào phương trình đã cho

Khi đó ta có: ( 2 + 2 )( 2 – m ) = 4 ⇔ 4( 2 – m ) = 4

⇔ 2 – m = 1 ⇔ m = 1.

Vậy m = 1 là giá trị cần tìm.

Chọn đáp án A.

Bài 5: Giá trị của m để phương trình x³ – x² = x + m có nghiệm x = 0 là?

A. m = 1.   

B. m = – 1.

C. m = 0.   

D. m = ± 1.

Lời giải:

Thay x = 0 vào phương trình x³ – x² = x + m.

Khi đó ta có: 0³ – 0² = 0 + m ⇔ m = 0.

Vậy m = 0 là giá trị cần tìm.

Chọn đáp án C.

Bài 6: Giải phương trình: x² – 5x + 6 = 0

A. x = 3 hoặc x = 2

B. x= -2 hoặc x = -3

C. x = 2 hoặc x = -3

D. x = -2 hoặc x = 3

Lời giải:

Chọn đáp án A

Bài 7: Số nghiệm của phương trình x² + 6x + 10 = 0

A. 1

B. 2

C. 0

D. Vô nghiệm

Lời giải:

Chọn đáp án D

Bài 8: Giải phương trình:

Lời giải:

Chọn đáp án B

Bài 9: Giải phương trình : 3x² + 6x – 9 = 0

A. x = 1

B. x = 1 hoặc x = -3

C. x = 1 hoặc x = -2

D. x = -3 hoặc x = -2

Lời giải:

Chọn đáp án B

Bài 10: Giải phương trình: 3(x – 2) + x² – 4 = 0

A. x = 1 hoặc x = 2

B. x = 2 hoặc x = -5

C. x = 2 hoặc x = – 3

D. Đáp án khác

Lời giải:

Vậy nghiệm của phương trình đã cho là x = 2 hoặc x = – 5

Chọn đáp án B

II. Bài tập tự luận có lời giải

Bài 1: Tích các nghiệm của phương trình x³ + 4x² + x – 6 = 0 là?

Lời giải

Ta có

x³ + 4x² + x – 6 = 0

⇔ x³ – x² + 5x² – 5x + 6x – 6 = 0

⇔ x(x – 1) + 5x(x – 1) + 6(x – 1) = 0

⇔ (x – 1)(x² + 5x + 6) = 0

⇔ (x – 1)(x² + 2x + 3x + 6) = 0

⇔ (x – 1)[x(x + 2) + 3(x + 2)] = 0

⇔ (x – 1)(x + 2)(x + 3)= 0

Vậy S = {1; -2; -3} nên tích các nghiệm là 1.(-2).(-3) = 6

Bài 2 Tích các nghiệm của phương trình x³ – 3x² – x + 3 = 0 là?

Lời giải

Ta có x³ – 3x² – x + 3 = 0

⇔ (x³ – 3x²⁾ – (x – 3) = 0

⇔ x(x² – 3) – (x – 3)= 0

⇔ (x – 3)(x² – 1) = 0

⇔ (x – 3)(x – 1)(x + 1) = 0

Vậy S = {1; -1; 3} nên tích các nghiệm là 1.(-1).3 = -3

Bài 3 Nghiệm lớn nhất của phương trình (x² – 1)(2x – 1) = (x² – 1)(x + 3) là?

Lời giải

Ta có (x² – 1)(2x – 1) = (x² – 1)(x + 3)

⇔ (x² – 1)(2x – 1) – (x² – 1)(x + 3) = 0

⇔ (x² – 1)(2x – 1 – x – 3) = 0

⇔ (x² – 1)(x – 4) = 0

Vậy tập nghiệm của phương trình S = {-1; 1; 4}

Nghiệm lớn nhất của phương trình là x = 4

Bài 4 Số nghiệm của phương trình: (x² + 9)(x – 1) = (x² + 9)(x + 3) là?

Lời giải

Ta có (x² + 9)(x – 1) = (x² + 9)(x + 3)

⇔ (x² + 9)(x – 1) – (x² + 9)(x + 3) = 0

⇔ (x² + 9)(x – 1 – x – 3) = 0

⇔ (x² + 9)(-4) = 0

⇔ x² + 9 = 0 ⇔ x² = -9 (vô nghiệm)

Vậy tập nghiệm của phương trình S = Ø hay phương trình không có nghiệm

Bài 5 Nghiệm nhỏ nhất của phương trình (2x + 1)² = (x – 1)² là?

Lời giải

Ta có (2x + 1)² = (x – 1)²

⇔ (2x + 1 + x – 1)(2x + 1 – x + 1) = 0

⇔ 3x(x + 2) = 0

Vậy tập nghiệm của phương trình S = {0; -2}

Nghiệm nhỏ nhất là x = -2

Bài 6 Giải các phương trình:

a) (3x – 2)(4x + 5) = 0

b) (2,3x – 6,9)(0,1x + 2) = 0

c) (4x + 2)(x²+ 1) = 0

d) (2x + 7)(x – 5)(5x + 1) = 0

Lời giải:

 

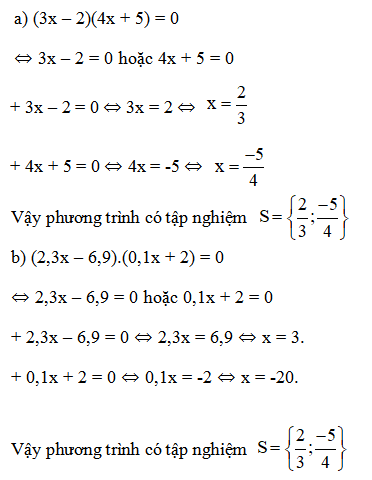
Bài 7 Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:

a) 2x(x – 3) + 5(x – 3) = 0;

b) (x²– 4) + (x – 2)(3 – 2x) = 0;

c) x³– 3x²+ 3x – 1 = 0;

d) x(2x – 7) – 4x + 14 = 0;

e) (2x – 5)²– (x + 2)²= 0;

f) x²– x – (3x – 3) = 0.

Lời giải:

a) 2x(x – 3) + 5(x – 3) = 0

⇔ (2x + 5)(x – 3) = 0

⇔ 2x + 5 = 0 hoặc x – 3 = 0

+ 2x + 5 = 0 ⇔2x = -5 ⇔ x = –$\frac{5}{2}$

+ x – 3 = 0 ⇔x = 3.

Vậy phương trình có tập nghiệm

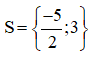
b) (x²– 4) + (x – 2)(3 – 2x) = 0

⇔ (x – 2)(x + 2) + (x – 2)(3 – 2x) = 0

⇔ (x – 2)[(x + 2) + (3 – 2x)] = 0

⇔ (x – 2)(5 – x) = 0

⇔ x – 2 = 0 hoặc 5 – x = 0

+ x – 2 = 0 ⇔ x = 2

+ 5 – x = 0 ⇔ x = 5.

Vậy tập nghiệm của phương trình là S = {2; 5}.

c) x³– 3x²+ 3x – 1 = 0

⇔ (x – 1)³ = 0 (Hằng đẳng thức)

⇔ x – 1 = 0

⇔ x = 1.

Vậy tập nghiệm của phương trình là S={1}.

d) x(2x – 7) – 4x + 14 = 0

⇔ x(2x – 7) – 2(2x – 7) = 0

⇔(x – 2)(2x – 7) = 0

⇔ x – 2 = 0 hoặc 2x – 7 = 0

+ x – 2 = 0 ⇔ x = 2.

+ 2x – 7 = 0 ⇔ 2x = 7 ⇔ x = $\frac{7}{2}$

Vậy tập nghiệm của phương trình là:

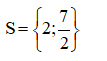
e) (2x – 5)²– (x + 2)²= 0

⇔ [(2x – 5) + (x + 2)].[(2x – 5) – (x + 2)]= 0

⇔ (3x – 3)(x – 7) = 0

⇔ 3x – 3 = 0 hoặc x – 7 = 0

+ 3x – 3 = 0 ⇔3x = 3 ⇔ x = 1.

+ x – 7 = 0 ⇔ x = 7.

Vậy phương trình có tập nghiệm S = {1; 7}.

f) x²– x – (3x – 3) = 0

⇔ x(x – 1) – 3(x – 1) = 0

⇔ (x – 3)(x – 1) = 0

⇔ x – 3 = 0 hoặc x – 1 = 0

+ x – 3 = 0 ⇔ x = 3

+ x – 1 = 0 ⇔ x = 1.

Vậy phương trình có tập nghiệm S = {1; 3}.

Bài 8 Phân tích đa thức P(x) = (x² – 1) + (x + 1)(x – 2) thành nhân tử.

Lời giải

P(x) = (x²– 1) + (x + 1)(x – 2)

P(x) = (x – 1) (x+1) + (x + 1)(x – 2)

P(x) = (x + 1) (x – 1 + x – 2)

P(x) = (x +1) (2x – 3)

Bài 9 Hãy nhớ lại một tính chất của phép nhân các số, phát biểu tiếp các khẳng định sau:

Trong một tích nếu có một thừa số bằng 0 thì …; ngược lại, nếu tích bằng 0 thì ít nhất một trong các thừa số của tích …

Lời giải

Trong một tích nếu có 1 thừa số bằng 0 thì tích bằng 0; ngược lại, nếu tích bằng 0 thì ít nhất 1 trong các thừa số của tích bằng 0

Bài 10 Giải phương trình:

(x – 1)(x² + 3x – 2) – (x³ – 1) = 0.

Lời giải

(x – 1)(x² + 3x – 2) – (x³ – 1) = 0

⇔ (x – 1)(x² + 3x – 2) – (x – 1)(x² + x + 1) = 0

⇔ (x – 1)[(x² + 3x – 2) – (x² + x + 1)] – 0

⇔ (x – 1)(2x – 3) = 0

⇔ x – 1 = 0 hoặc 2 – 3 = 0

x – 1 = 0 ⇔x = 1

2x – 3 = 0 ⇔x = $\frac{3}{2}$

Vậy tập nghiệm của phương trình là S = {1;$\frac{3}{2}$}

III. Bài tập vận dụng

Bài 1 Phân tích đa thức P(x) = (x² – 1) + (x + 1)(x – 2) thành nhân tử.

Bài 2 Hãy nhớ lại một tính chất của phép nhân các số, phát biểu tiếp các khẳng định sau: Trong một tích nếu có một thừa số bằng 0 thì …; ngược lại, nếu tích bằng 0 thì ít nhất một trong các thừa số của tích …

Bài 3 Giải phương trình: (x – 1)(x² + 3x – 2) – (x³ – 1) = 0.

Bài 4 Giải phương trình (x³ + x²) + (x² + x) = 0.

Bài 5 Giải các phương trình:

a) (3x – 2)(4x + 5) = 0

b) (2,3x – 6,9)(0,1x + 2) = 0

c) (4x + 2)(x² + 1) = 0

d) (2x + 7)(x – 5)(5x + 1) = 0

Bài 6 Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:

Bài 7 Giải các phương trình:

a) x(2x – 9) = 3x(x – 5)

b, 0,5x(x – 3) = (x – 3)(1,5x – 1)

c) 3x – 15 = 2x(x – 5)

d) 

Bài 8 Giải các phương trình:

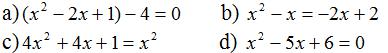
Bài 9 Giải các phương trình:

a) 2x³ + 6x² = x² + 3x

b) (3x – 1)(x² + 2) = (3x – 1)(7x – 10)

Bài 10 Giải các phương trình:

a) $(3x-2)(4x+5)=0$

b) $(2,3x-6,9)(0,1x+2)=0$

c) $(4x+2)(x^2+1)=0$

d) $(2x+7)(x-5)(5x+1)=0$

B. Lý thuyết Phương trình tích

Chú ý rằng:

1. Phương trình   $A\left(x\right).B\left(x\right)=0\iff \left[\begin{array}{l}A\left(x\right)=0\\ B\left(x\right)=0\end{array}\right.$

2. Mở rộng, phương trình $A\left(x\right).B\left(x\right)\dots M\left(x\right)=0\iff \left[\begin{array}{l}A\left(x\right)=0\\ B\left(x\right)=0\\ \dots \\ M\left(x\right)=0\end{array}\right.$