50 Bài tập Phân tích đa thức thành nhân tử bằng phương pháp hằng đẳng thức (có đáp án)- Toán 8

Bài tập Toán 8 Chương 1 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp hằng đẳng thức

A. Bài tập Phân tích đa thức thành nhân tử bằng phương pháp hằng đẳng thức 

Bài 1: Phân tích đa thức thành nhân tử

          a) $x^2-x+\frac{1}{4}$                                        b) $2x^3-12x^2+24x-16$

          c) ${\left(x+y\right)}^3-{\left(x-y\right)}^3$                              c) $2x^4+2x^2+2$

Lời giải:       

  a) Ta có: $x^2-x+\frac{1}{4}=x^2-2\frac{1}{2}x+\frac{1}{4}={\left(x-\frac{1}{2}\right)}^2$

          b) Ta có: $2x^3-12x^2+24x-16=2\left(x^3-6x^2+12x-8\right)$

          $=2\left(x^3-3.x^2.2+\mathrm{3.4.}x-2^3\right)=2{\left(x-2\right)}^3$        

          c) Ta có: ${\left(x+y\right)}^3-{\left(x-y\right)}^3$

            $=\left(x^3+3x^{2}y+3x{y}^2+y^3\right)-\left(x^3-3x^{2}y+3x{y}^2-y^3\right)$      

         $=6x^{2}y+2y^3=2y\left(3x^2+y^2\right)$

d) Ta có: $2x^4+2x^2+2=2\left(x^4+x^2+1\right)=2\left(x^4+2x^2+1-x^2\right)$

$=2\left({\left(x^2+1\right)}^2-x^2\right)=2\left(\left(x^2+1-x\right)\left(x^2+1+x\right)\right)$

Bài 2: Phân tích đa thức thành nhân tử

          a)  $x^4+4$                                             b) $x^3+6x^2-16$

          c)  $\frac{1}{36}{a}^2-\frac{1}{4}{b}^2$                                     d) $x^2+2x-y^2+2y$

Lời giải:   

          a) Ta có: $x^4+4=x^4+4x^2+4-4x^2={\left(x^2+4\right)}^2-4x^2$

           $=\left(x^2+4-2x\right)\left(x^2+4+2x\right)=\left(x^2-2x+4\right)\left(x^2+2x+4\right)$       

          b) Ta có: $x^3+6x^2-16=x^3+6x^2+12x+8-12x-24$

           $={\left(x+2\right)}^3-12\left(x+2\right)=\left(x+2\right)\left({\left(x+2\right)}^2-12\right)=\left(x+2\right)\left(x^2+4x-8\right)$       

          c) Ta có: $\frac{1}{36}{a}^2-\frac{1}{4}{b}^2={\left(\frac{1}{6}a\right)}^2-{\left(\frac{1}{2}b\right)}^2=\left(\frac{1}{6}a+\frac{1}{2}b\right).\left(\frac{1}{6}a-\frac{1}{2}b\right)$

Bài 3: Phân tích các đa thức sau thành nhân tử:

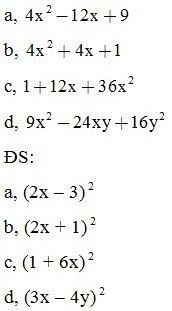
Bài 4: Phân tích các đa thức sau thành nhân tử:

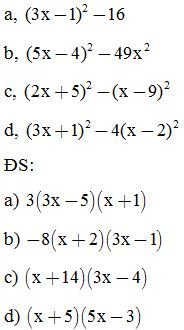
Bài 5: Phân tích các đa thức sau thành nhân tử:

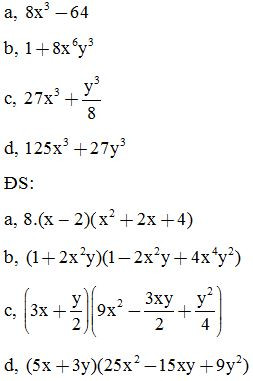
Bài 6: Phân tích các đa thức sau thành nhân tử:

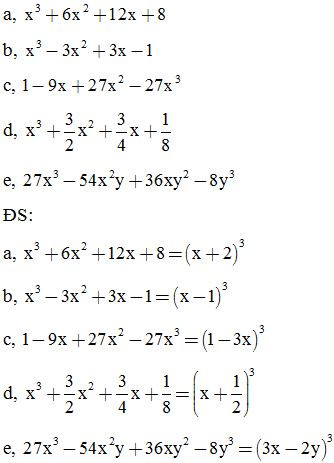
Bài 7: Phân tích các đa thức sau thành nhân tử:

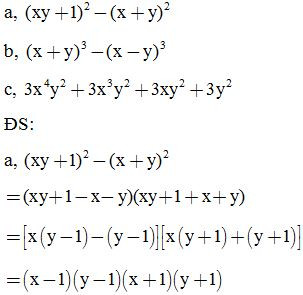
Bài 8: Phân tích các đa thức sau thành nhân tử

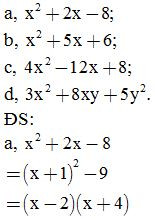
Bài 9: Tìm x, biết

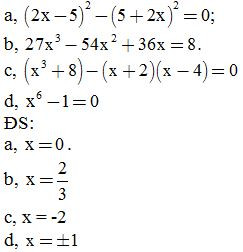
Bài 10: Chứng minh

a, $2^9-1$ chia hết cho 73

b, $5^6-{10}^4$ chia hết cho 9

c, ${\left(n+3\right)}^2-{\left(n-1\right)}^2$ chia hết cho 8 với mọi số tự nhiên n

d, ${\left(n+6\right)}^2-{\left(n-6\right)}^2$ chia hết cho 24 với mọi số tự nhiên n

ĐS:

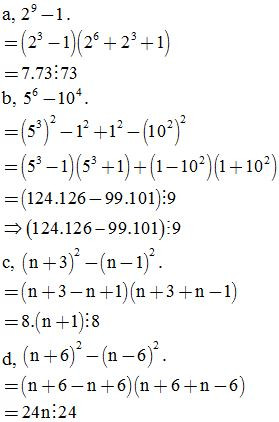
Bài 11: Tính nhanh

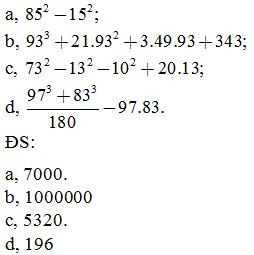
B. Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp hằng đẳng thức 

Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

 

 Khi áp dụng phương pháp dùng hằng đẳng thức để phân tích đa thức thành nhân tử, ta cần lưu ý:

– Trước tiên nhận xét xem các hạng tử của đa thức có chứa nhân tử chung không, nếu có thì áp dụng phương pháp đặt thành nhân tử chung.

– Nếu không thì ta có thể sử dụng các hằng đẳng thức sau đây để phân tích đa thức thành nhân tử:

1) (A + B)² = A² + 2AB + B²

2) (A – B)² = A² – 2AB + B²

3) A² –  B² = (A – B)(A + B)

4) (A + B)³ = A³ + 3A²B + 3AB² + B³

5) (A – B)³ = A³ – 3A²B + 3AB² – B³

6) A³ + B³ = (A + B)(A² – AB + B²)

7) A³ – B³ = (A – B)(A² + AB + B²)

 

Ví dụ: Phân tích đa thức x³ + 3x² + 3x – 7 thành nhân tử.

Lời giải:

x³ + 3x² + 3x – 7

= x³ + 3x² + 3x + 1  – 8

= (x + 1)³ – 2³

= (x + 1 – 2)[(x + 1)² + 2.(x + 1) + 2²]

= (x – 1)(x² + 2x + 1 + 2x + 2 + 4)

= (x – 1)(x² + 4x + 7).

Xem thêm