Bài tập Toán 8 Chương 4 Bài 1: Liên hệ giữa thứ tự và phép cộng
A. Bài tập Liên hệ giữa thứ tự và phép cộng
I. Bài tập trắc nghiệm
Bài 1: Trong các khẳng định sau đây, khẳng định nào đúng?
4 + ( – 3 ) ≤ 5 ( 1 )
6 + ( – 2 ) ≤ 7 + ( – 2 ) ( 2 )
24 + ( – 5 ) > 25 + ( – 5 ) ( 3 )
A. ( 1 ),( 2 ),( 3 )
B. ( 1 ),( 3 )
C. ( 1 ),( 2 )
D. ( 2 ),( 3 )
Lời giải:
+ Ta có: -3 < 1 nên 4 + (-3) < 4 + 1 hay 4 + (-3) < 5
Khẳng định ( 1 ) đúng.
+ Ta có: 6 < 7 nên 6 + (-2) < 7 + (-2)
Khẳng định ( 2 ) đúng.
+ Ta có: 24 < 25 ⇒ 24 + ( – 5 ) < 25 + ( – 5 )
→ Khẳng định ( 3 ) sai.
Chọn đáp án C.
Bài 2: Cho a – 3 > b – 3. So sánh hai số a và b
A. a ≥ b
B. a < b
C. a > b
D. a ≤ b
Lời giải:
Ta có a – 3 > b – 3 ⇒ ( a – 3 ) + 3 > ( b – 3 ) + 3 ⇔ a > b
Chọn đáp án C.
Bài 3: Cho a > b. So sánh 5 – a với 5 – b
A. 5 – a ≥ 5 – b.
B. 5 – a > 5 – b.
C. 5 – a ≤ 5 – b.
D. 5 – a < 5 – b.
Lời giải:
Ta có: a > b ⇒ – a < – b ⇔ 5 + ( – a ) < 5 + ( – b ) hay 5 – a < 5 – b.
Chọn đáp án D.
Bài 4: Một Ampe kế có giới hạn đo là 25 ampe. Gọi x( A ) là số đo cường độ dòng điện có thể đo bằng Ampe kế. Khẳng định nào sau đây đúng?
A. x ≤ 25
B. x < 25
C. x > 25
D. x ≥ 25
Lời giải:
Một Ampe kế đo cường độ dòng điện thì cường độ dòng điện tối đa mà Ampe đo được là giới hạn đo của ampe kế đó.
Khi đó: x ≤ 25
Chọn đáp án A.
Bài 5: Cho a > b, c > d. Khẳng định nào sau đây đúng?
A. a + d > b + c
B. a + c > b + d
C. b + d > a + c
D. a + b > c + d
Lời giải:
Theo giả thiết ta có: a > b, c > d ⇒ a + c > b + d.
Chọn đáp án B.
Bài 6: Cho a < b. So sánh: a + (-3) và b + 3
A. a + (-3) = b + 3
B. a + (-3) > b +3
C. a + (-3) < b +3
D. Không so sánh được.
Lời giải:
* Ta có: a < b nên a + (-3) < b + (-3) (1)
Lại có: – 3 < 3 nên b +(-3) < b +3 (2)
* Từ (1) và (2) suy ra a + (-3) < b +3
Chọn đáp án C
Bài 7: Cho a + 2 < b – 3 . So sánh a và b?
A. a < b
B. a > b
C. a = b
D. Chưa thể kết luận
Lời giải:
Ta có : a + 2 < b – 3 nên a + 2+ (-2) < b – 3 + (-2)
Hay a < b – 5 (1)
Lại có: -5 < 0 nên b – 5 < b (2)
Từ (1) và (2) suy ra: a < b
Chọn đáp án A
Bài 8: Cho các khẳng định sau:
(1): 3 + ( -10) < 4 + (- 10)
(2): (-2) + (-15) > (-2) + (-13)
(3): 4 – 9 < -5 – 9
Hoỉ có bao nhiêu khẳng định đúng?
A. 0
B. 1
C. 2
D. 3
Lời giải:
(1): Vì 3 < 4 nên 3 + ( -10) < 4 + (- 10)
Do đó (1) đúng.
(2): vì (- 15) < (-13) nên (-2) + (-15) < (-2) + (-13)
Suy ra (2) sai
(3): Ta có: 4 > – 5 nên 4+ (-9) > – 5 + (- 9) hay 4 – 9 > -5 – 9
Suy ra (3) sai
Vậy chỉ có 1 khẳng định đúng
Chọn đáp án B
Bài 9: Cho a < b – 1. So sánh a và b.
A. Chưa thể kết luận
B. a = b
C. a > b
D. a < b
Lời giải:
Ta có: -1 < 0 nên b + (-1) < b + 0 hay b – 1 < b (1)
Lại có: a < b – 1 (giả thiết ) (2 )
Từ (1) và (2) suy ra: a < b
Chọn đáp án D
Bài 10: Ta có:
(1) -2000 < -2001
(2) suy ra: -2000 + a < -2001 + a
Bài giải trên có sai không? Nếu sai thì sai từ bước mấy?
A. Bài giải đúng
B. Sai bước 1
C. Sai bước 2
D. Tùy giá trị của a.
Lời giải:
Ta có: -2000 > -2001 nên bước (1) sai
Chọn đáp án B
II. Bài tập tự luận có lời giải
Bài 1: Cho a > b khi đó?
Lời giải
Từ a > b, cộng -b vào hai vế ta được a – b > b – b, tức là a – b > 0.
Bài 2 Cho a > 1 > b, chọn khẳng định không đúng?
Lời giải
Từ a > b, cộng -b vào hai vế ta được a – b > b – b, tức là a – b > 0.
Do đó D đúng, B sai.
Ngoài ra A, C đúng vì:
Cộng cả hai vế của bất đẳng thức a > 1 với (-1) ta được:
a + (-1) > 1 + (-1) hay a – 1 > 0.
Cộng cả hai vế của bất đẳng thức 1 > b với -b ta được:
1 + (-b) > b + (-b) hay 1 – b > 0.
Đáp án cần chọn là: B
Bài 3 So sánh m và n biết m – = n?
Lời giải
Ta có: m – = n ⇒ m – n =
⇒ m – n > 0 ⇒ m > n.
Bài 4 So sánh m và n biết m + = n?
Lời giải
Ta có: m + = n ⇒ m – n = –
⇒ m – n < 0 ⇒ m < n.
Bài 5 Cho a + 8 < b. So sánh a – 7 và b – 15?
Lời giải
Cộng cả hai vế của bất đẳng thức a + 8 < b với (-15) ta được
a + 8 < b ⇒ a + 8 – 15 < b – 15 ⇒ a – 7 < b – 15
Bài 6 Cho a – 3 < b. So sánh a + 10 và b + 13?
Lời giải
Cộng cả hai vế của bất đẳng thức a – 3 < b với 13 ta được:
a – 3 < b ⇒ a – 3 + 13 < b + 13 ⇒ a + 10 < b + 13.
Bài 7 Mỗi khẳng định sau đúng hay sai? Vì sao?
a) (-2) + 3 ≥ 2;
b) -6 ≤ 2.(-3);
c) 4 + (-8) < 15 + (-8);
d) x2+ 1 ≥ 1.
Lời giải:
(Kí hiệu: VP = vế phải; VT = vế trái)
a) Ta có: (-2) + 3 = 1
Vì 1 < 2 nên (-2) + 3 < 2.
Do đó khẳng định (-2) + 3 ≥ 2 là sai.
b) Ta có: 2.(-3) = -6
⇒ Khẳng định -6 ≤ 2.(-3) là đúng.
c) Ta có: 4 + (-8) = -4
15 + (-8) = 7
Vì -4 < 7 nên 4 + (-8) < 15 + (-8)
Do đó khẳng định c) đúng
d) Với mọi số thực x ta có: x2≥ 0
⇒ x2 + 1 ≥ 1
⇒ Khẳng định d) đúng với mọi số thực x.
Bài 8 Cho a < b, hãy so sánh:
a) a + 1 và b + 1 ;
b) a – 2 và b – 2
Lời giải:
a) a < b
⇒ a + 1 < b + 1
(Cộng cả hai vế của BĐT với 1).
c) a < b
⇒ a + (-2) < b + (-2)
(Cộng cả hai vế của BĐT với -2).
hay a – 2 < b – 2.
Bài 9 So sánh a và b nếu:
a) a – 5 ≥ b – 5 ; b) 15 + a ≤ 15 + b
Lời giải:
a) Vì a – 5 ≥ b – 5
=> a – 5 + 5 ≥ b – 5 + 5 (cộng 5 vào hai vế)
=> a ≥ b
b) 15 + a ≤ 15 + b
=> 15 + a + (-15) ≤ 15 + b (-15) (cộng -15 vào hai vế)
=> a ≤ b
III. Bài tập vận dụng
Bài 1 Một biển báo giao thông với nền trắng, số 20 màu đen, viền đỏ (xem minh họa ở hình bên) cho biết vận tốc tối đa mà các phương tiện giao thông được đi trên quãng đường có biển quy định là 20km/h. Nếu một ô tô đi trên đường đó có vận tốc là a (km/h) thì a phải thỏa mãn điều kiện nào trong các điều kiện sau? a > 20 ; a < 20 ; a ≤ 20 ; a ≥ 20
Bài 2 So sánh a và b nếu:
a) a – 5 ≥ b – 5 ; b) 15 + a ≤ 15 + b
Bài 3 Cho a < b, hãy so sánh:
a) a + 1 và b + 1 ;
b) a – 2 và b – 2
Bài 4 Mỗi khẳng định sau đúng hay sai? Vì sao?
a) (-2) + 3 ≥ 2;
b) -6 ≤ 2.(-3);
c) 4 + (-8) < 15 + (-8);
d) x2 + 1 ≥ 1.
Bài 5 Dựa vào thứ tự và 3, hãy so sánh + 2 và 5.
Bài 6 So sánh – 2004 + (- 777) và – 2005 + (- 777) mà không tính giá trị của từng biểu thức.
a) Khi cộng – 3 và cả hai vế của bất đẳng thức – 4 < 2 thì được bất đẳng thức nào ?
b) Dự đoán kết quả: Khi cộng số c vào cả hai vế của bất đẳng thức – 4 < 2 thì được bất đẳng thức nào ?
Bài 7 So sánh a và b nếu:
a)
b)
Bài 8 Cho tam giác ABC. Các khẳng định sau đúng hay sai?
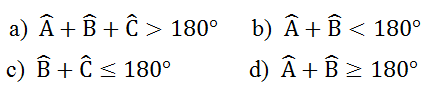
a) So sánh (-2).3 và -4,5.
b) Từ kết quả câu a) hãy suy ra các bất đẳng thức sau:
(-2).30 < -45 ; (-2).3 + 4,5 < 0
B. Lý thuyết Liên hệ giữa thứ tự và phép cộng
1. Thứ tự trên tập hợp số
– Mối quan hệ giữa các tập hợp
– Biểu đồ Venn
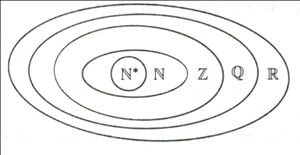
– So sánh hai số a và b trên tập số thực
|
Ký hiệu |
Cách đọc |
|
a = b |
a bằng b |
|
a > b |
a lớn hơn b |
|
a < b |
a nhỏ hơn b |
|
a ≥ b |
a lớn hơn hoặc bằng b hoặc a không nhỏ hơn b |
|
a ≤ b |
a nhỏ hơn hoặc bằng b hoặc a không lớn hơn b |
Chú ý: với mọi A;
với mọi A;
với mọi A là số thực
với mọi A là số thực
2. Bất đẳng thức
– Hệ thức dạng được gọi là bất đẳng thức; trong đó a và b lần lượt được gọi là vế trái và vế phải.
– Khi cộng cùng một số vào cả hai vế của một bất đẳng thức, ta được bất đẳng thức mới cùng chiều và bất đẳng thức đã cho, cụ thể như sau:
+ Nếu a > b thì a + c > b + c;
+ Nếu a < b thì a + c < b + c;
+ Nếu a ≥ b thì a + c ≥ b + c;
+ Nếu a ≤ b thì a + c ≤ b + c.