Vở bài tập Toán 7 Bài 3: Hai tam giác bằng nhau – Cánh diều

Giải VBT Toán lớp 7 Bài 3: Hai tam giác bằng nhau

I. Kiến thức trọng tâm

Câu 1 trang 77 vở bài tập Toán lớp 7 Tập 2:

– Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng………. và các góc tương ứng………….

– Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta kí hiệu là: ………………………

(Hình 20)

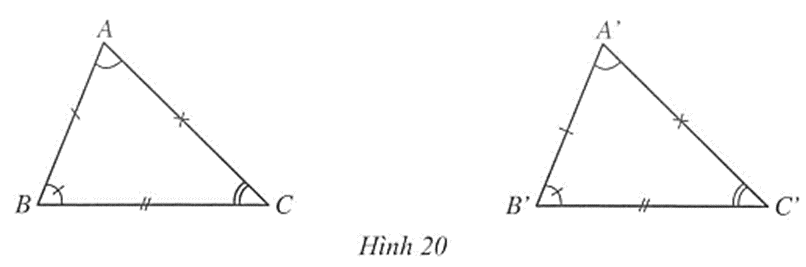
Quy ước: Khi viết hai tam giác bằng nhau, tên đỉnh của hai tam giác đó phải viết theo đúng thứ tự tương ứng với sự bằng nhau.

+ Nếu AB = A’B’, BC = B’C’, CA = C’A’ và $\hat{A}=\widehat{A‘}$, $\hat{B}=\widehat{B‘}$, $\hat{C}=\widehat{C‘}$ thì ∆ABC = …

+ Nếu ∆ABC = ∆A’B’C’ thì AB = …., …. = B’C’, CA = …. và ….= $\widehat{A‘}$, $\hat{B}$=…., …= $\hat{C}‘$

Lời giải:

– Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau.

– Khi hai tam giác ABC và A’B’C’ bằng nhau thì ta kí hiệu là: ∆ABC = ∆A’B’C’.

+ Nếu AB = A’B’, BC = B’C’, CA = C’A’ và $\hat{A}=\widehat{A‘}$, $\hat{B}=\widehat{B‘}$, $\hat{C}=\widehat{C‘}$ thì ∆ABC = ∆A’B’C’.

+ Nếu ∆ABC = ∆A’B’C’ thì AB = A’B’, BC = B’C’, CA = C’A’ và $\hat{A}=\widehat{A‘}$, $\hat{B}=\widehat{B‘}$, $\hat{C}=\widehat{C‘}$.

II. Luyện tập

• Câu 1 trang 77 vở bài tập Toán lớp 7 Tập 2:Cho ∆ABC = ∆MNP, AC = 4 cm, $\widehat{\mathrm{MPN}}$ = 45^o. Tính độ dài cạnh MP và số đo góc ACB.

  Lời giải:

  Vì ∆ABC = ∆MNP nên

  AC = MP (hai cạnh tương ứng); $\widehat{\mathrm{ACB}}$ = $\widehat{\mathrm{MPN}}$(hai góc tương ứng)

  Mà AC = 4 cm và $\widehat{\mathrm{MPN}}$ = 45^o nên MP = 4 cm, $\widehat{\mathrm{ACB}}$= 45^o.

• III. Bài tập

  • Câu 1 trang 77 vở bài tập Toán lớp 7 Tập 2:Cho biết ∆ABC = ∆DEG, AB = 3cm, BC = 4 cm, CA = 6 cm. Tính độ dài các cạnh của tam giác DEG

    Lời giải:

    Vì ∆ABC = ∆DEG nên AB = DE, BC = EG, CA = GD

    Mà AB = 3cm, BC = 4 cm, CA = 6 cm nên DE = 3 cm, EG = 4 cm, GD = 6 cm.

  • Câu 2 trang 77 vở bài tập Toán lớp 7 Tập 2:Cho ∆PQR = ∆IHK, $\hat{P}$ = 71^o, $\hat{Q}$ = 49^o. Tính số đo góc K của tam giác IHK.

    Lời giải:

    Ta có: $\hat{P}$+ $\hat{Q}$+ $\hat{R}$= 180^o (tổng ba góc của một tam giác), $\hat{P}$ = 71^o, $\hat{Q}$ = 49^o.

    Suy ra: $\hat{R}$= 180^o – ( $\hat{P}$+ $\hat{Q}$ ) = 180^o – (71^o + 49^o) = 60^o

    Do ∆PQR = ∆IHK nên $\hat{R}$= $\hat{K}$(hai góc tương ứng). Suy ra $\hat{K}$= 60^o.

  • Câu 3 trang 78 vở bài tập Toán lớp 7 Tập 2:Cho ∆ABC = ∆MNP và $\hat{A}$+ $\hat{N}$= 125^o. Tính số đo góc P.

    Lời giải:

    Vì ∆ABC = ∆MNP nên $\hat{A}$= $\hat{M}$( hai góc tương ứng)

    Do $\hat{A}$+ $\hat{N}$= $\hat{M}$+ $\hat{N}$Mà $\hat{A}$+ $\hat{N}$= 125^o nên $\hat{M}$+ $\hat{N}$= 125^o.

    Ta có $\hat{M}$+ $\hat{N}$+ $\hat{P}$= 180^o (tổng ba góc của một tam giác)

    Suy ra 125^o + $\hat{P}$= 180^o vì thế $\hat{P}$= 180^o – 125^o = 55^o.

  • Câu 4 trang 78 vở bài tập Toán lớp 7 Tập 2:Cho tam giác ABC và điểm M thuộc cạnh BC thoả mãn ∆AMB = ∆AMC (Hình 21). Chứng minh rằng:

    a) M là trung điểm của đoạn thẳng BC;

    b) Tia AM là tia phân giác của góc BAC và AM $\perp$ BC.

    Lời giải:

    Vì ∆AMB = ∆AMC nên: MB = MC (hai cạnh tương ứng);

    $\widehat{\mathrm{BAM}}$= $\widehat{\mathrm{CAM}}$, $\widehat{\mathrm{AMB}}$= $\widehat{\mathrm{AMC}}$(hai góc tương ứng)

    a) Do điểm M nằm giữa hai điểm B, C và MB = MC nên M là trung điểm của đoạn thẳng BC.

    b) Do tia AM nằm trong góc BAC và $\widehat{\mathrm{BAM}}$= $\widehat{\mathrm{CAM}}$nên tia AM là tia phân giác của góc BAC

    Ta có $\widehat{\mathrm{AMB}}$+ $\widehat{\mathrm{AMC}}$= 180^o (hai góc kề bù) và $\widehat{\mathrm{AMB}}$= $\widehat{\mathrm{AMC}}$nên $\widehat{\mathrm{AMB}}$= $\widehat{\mathrm{AMC}}$= 90^o.

    Vậy AM $\perp$ BC.

  • Câu 5 trang 78 vở bài tập Toán lớp 7 Tập 2: Cho Hình 22, ở đó ∆OAB = ∆OCD. Chứng minh a // b.

    

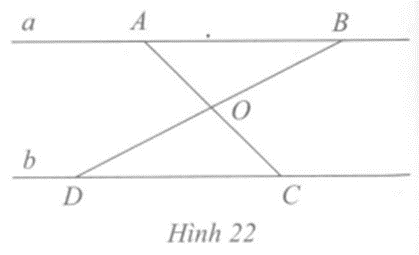
    Lời giải:

    Ta có ∆OAB = ∆OCD nên $\widehat{\mathrm{OAB}}$= $\widehat{\mathrm{OCD}}$

    Lại có $\widehat{\mathrm{OAB}}$và $\widehat{\mathrm{OCD}}$là hai góc so le trong

    Suy ra a // b.