Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Phân loại và phương pháp giải bài tập vectơ trong không gian, quan hệ vuông góc
BÀI 1. VECTO TRONG KHÔNG GIAN
A. Kiến thức cơ bản cần nắm
I. Định nghĩa và các phép toán về vectơ trong không gian
Cho đoạn thẳng trong không gian. Nếu ta chọn điểm đầu là A, điểm cuối là B ta có một vectơ, được kí hiệu là \[\overrightarrow {AB} \].
Định nghĩa
Vectơ trong không gian là một đoạn thẳng có hướng. Kí hiệu \[\overrightarrow {AB} \] chỉ vectơ có điểm đầu là A, điểm cuối B. Vectơ còn được kí hiệu là \[\overrightarrow a ,\overrightarrow b ,\overrightarrow x ,\overrightarrow y \],…
Các khái niệm có liên quan đến vectơ như giá của vectơ, độ dài của vectơ, sự cùng phương, cùng hướng của hai vectơ, vectơ – không, sự bằng nhau của hai vectơ, … được định nghĩa tương tự như trong mặt phẳng.
II. Điều kiện đồng phẳng của ba vectơ
1. Khái niệm về sự đồng phẳng của ba vectơ trong không gian
Trong không gian cho ba vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] đều khác vectơ – không. Nếu từ một điểm O bất kì ta vẽ \[\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c \] thì có thể xả ra hai trường hợp:
Trường hợp các đường thẳng OA, OB, OC không cùng nằm trong một mặt phẳng, khi đó ta nói rằng vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] không đồng phẳng.
Trường hợp các đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng thi ta nói ba vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \]đồng phẳng.
Trong trường hợp này giá của các vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \]luôn luôn song song với một mặt phẳng.
a) Ba vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] không đồng phẳng

b) Ba vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] đồng phẳng

Chú ý. Việc xác định sự đồng phẳng hoặc không đồng phẳng của ba vectơ nói trên không phụ thuộc vào việc chọn điểm O.
Từ đó ta có định nghĩa sau đây:
2. Định nghĩa
Trong không gian ba vectơ được gọi là đồng phẳng nếu các giá của chúng cùng song song với một mặt phẳng.
3. Điều kiện để ba vectơ đồng phẳng
Từ định nghĩa ba vectơ đồng phẳng và từ định lí về sự phân tích (hay biểu thị) một vectơ theo hai vectơ hai vectơ không cùng phương trong hình học phẳng chúng ta có thể chứng minh được định lí sau đây:
Định lí 1
Trong không gian cho hai vectơ \[\overrightarrow a ,\overrightarrow b \] không cùng phương và vectơ \[\overrightarrow c \]. Khi đó ba vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \] đồng phẳng khi và chỉ khi có cặp số m, n sao cho \[\overrightarrow c = m\overrightarrow a + n\overrightarrow b \]. Ngoài ra cặp số m, n là duy nhất.
Định lí 2
Trong không gian cho ba vectơ không đồng phẳng \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \]. Khi đó với mọi vectơ \[\overrightarrow x \] ta đều tìm được một bộ ba số m, n, p sao cho \[\overrightarrow x = m\overrightarrow a + n\overrightarrow b + p\overrightarrow c \]. Ngoài ra bộ ba số m, n, p là duy nhất.
B. Phân loại và phương pháp giải bài tập
Dạng 1. Biểu diễn vectơ
Câu 1: Cho hình lăng trụ \[ABC.A’B’C’\] . Đặt \[\overrightarrow a = \overrightarrow {AA} ‘,\overrightarrow b = \overrightarrow {AB} ,\overrightarrow c = \overrightarrow {AC} \]. Gọi G’ là trọng tâm của tam giác \[A’B’C’\]. Vectơ \[\overrightarrow {AG’} \] bằng:
A. \[\frac{1}{3}\left( {\overrightarrow a + 3\overrightarrow b + \overrightarrow c } \right)\]
B. \[\frac{1}{3}\left( {3\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\]
C. \[\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + 3\overrightarrow c } \right)\]
D. \[\frac{1}{3}\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)\]
Lời giải
Chọn B

Gọi I là trung điểm của B’C’ .
Vì G’ là trọng tâm của tam giác \[A’B’C’\] Þ \[\overrightarrow {A’G’} = \frac{2}{3}\overrightarrow {A’I} \].
Ta có \[\overrightarrow {AG’} = \overrightarrow {AA’} + \overrightarrow {A’G’} = \overrightarrow {AA’} + \frac{1}{3}\left( {\overrightarrow {A’B’} + \overrightarrow {A’C’} } \right)\]
\[\begin{array}{l} = \overrightarrow {AA’} + \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\\ = \frac{1}{3}\left( {3\overrightarrow {AA’} + \overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\left( {3\overrightarrow a + \overrightarrow b + \overrightarrow b } \right)\end{array}\]
Câu 2: Cho hình lăng trụ \[ABC.A’B’C’\]. Đặt \[\overrightarrow a = \overrightarrow {AA} ‘,\overrightarrow b = \overrightarrow {AB} ,\overrightarrow c = \overrightarrow {AC} \]. Hãy biểu diễn vectơ \[\overrightarrow {B’C} \] theo các vectơ \[\overrightarrow a ,\overrightarrow b ,\overrightarrow c \]
A. \[\overrightarrow {B’C} = \overrightarrow a + \overrightarrow b – \overrightarrow c \]
B. \[\overrightarrow {B’C} = – \overrightarrow a + \overrightarrow b – \overrightarrow c \]
C. \[\overrightarrow {B’C} = \overrightarrow a + \overrightarrow b + \overrightarrow c \]
D. \[\overrightarrow {B’C} = – \overrightarrow a – \overrightarrow b + \overrightarrow c \]
Lời giải
Chọn D
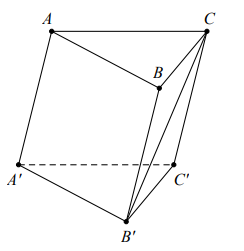
Vì \[BB’C’C\] là hình bình hành suy ra
\[\overrightarrow {B’C} = \overrightarrow {B’C’} + \overrightarrow {B’B} = \overrightarrow {BC} – \overrightarrow {AA’} \]
\[\begin{array}{l} = – \overrightarrow {AA’} + \overrightarrow {BA} + \overrightarrow {AC} = – \overrightarrow {AA’} – \overrightarrow {AB} + \overrightarrow {AC} \\ = – \overrightarrow a – \overrightarrow b + \overrightarrow c \end{array}\]
Câu 3: Cho hình lăng trụ \[ABC.A’B’C’\]. Gọi là trung điểm của BB’. Đặt \[\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {AA’} = \overrightarrow c \]. Khẳng định nào dưới đây là đúng?
A. \[\overrightarrow {AM} = \overrightarrow a + \overrightarrow c – \frac{1}{2}\overrightarrow b \]
B. \[\overrightarrow {AM} = \overrightarrow b – \overrightarrow c + \frac{1}{2}\overrightarrow a \]
C. \[\overrightarrow {AM} = \overrightarrow b – \overrightarrow a + \frac{1}{2}\overrightarrow c \]
D. \[\overrightarrow {AM} = \overrightarrow a – \overrightarrow c + \frac{1}{2}\overrightarrow b \]
Lời giải
Chọn C
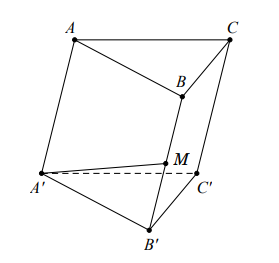
Vì M là trung điểm của \[\overrightarrow {BB’} \Rightarrow \overrightarrow {BM} = \frac{1}{2}\overrightarrow {BB’} \]
Ta có
\[\begin{array}{l}\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = – \overrightarrow {BA} + \frac{1}{2}\overrightarrow {BB’} \\ = – \overrightarrow {CA} + \overrightarrow {CB} + \frac{1}{2}\overrightarrow {BB’} = – \overrightarrow a + \overrightarrow b + \frac{1}{2}\overrightarrow c \end{array}\]
Câu 4: Cho hình hộp\[ABCD.A’B’C’D’\] tâm O. Gọi I là tâm của hình hình hành DBCD. Đặt \[\overrightarrow {AC’} = \overrightarrow u ,\overrightarrow {CA’} = \overrightarrow v ,\overrightarrow {BD’} = \overrightarrow x ,\overrightarrow {DB’} = \overrightarrow y \]. Khi đó
A. \[2\overrightarrow {OI} = – \frac{1}{4}\left( {\overrightarrow u + \overrightarrow v + \overrightarrow x + \overrightarrow y } \right)\]
B. \[2\overrightarrow {OI} = – \frac{1}{2}\left( {\overrightarrow u + \overrightarrow v + \overrightarrow x + \overrightarrow y } \right)\]
C. \[2\overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow u + \overrightarrow v + \overrightarrow x + \overrightarrow y } \right)\]
D. \[2\overrightarrow {OI} = \frac{1}{4}\left( {\overrightarrow u + \overrightarrow v + \overrightarrow x + \overrightarrow y } \right)\]
Lời giải
Chọn A
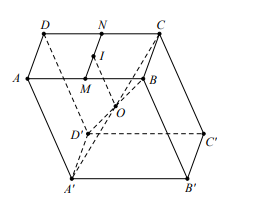
Gọi M, N lần lượt là trung điểm của AB, CD.
Vì I là trung điểm của MN suy ra \[\overrightarrow {OM} + \overrightarrow {ON} = 2\overrightarrow {OI} \].
Kết hợp với \[\left\{ {\begin{array}{*{20}{c}}{\overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OM} }\\{\overrightarrow {OC} + \overrightarrow {OD} = 2\overrightarrow {ON} }\end{array}} \right.\]
\[\begin{array}{l} \Rightarrow 2\overrightarrow {OI} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\\ = \frac{1}{2}\left( { – \frac{1}{2}\overrightarrow {AC’} – \frac{1}{2}\overrightarrow {CA’} – \frac{1}{2}\overrightarrow {BD’} – \frac{1}{2}\overrightarrow {DB’} } \right)\\ = – \frac{1}{4}\left( {\overrightarrow u + \overrightarrow v + \overrightarrow x + \overrightarrow y } \right)\end{array}\]
Câu 5: Cho hình hộp \[ABCD.A’B’C’D’\] có \[\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b ,\overrightarrow {AA’} = \overrightarrow c \]. Gọi I là trung điểm của B’C’. K là giao điểm của A’I và B’D’. Mệnh đều nào sau đây đúng?
A. \[\overrightarrow {DK} = \frac{1}{3}\left( {4\overrightarrow a – 2\overrightarrow b + 3\overrightarrow c } \right)\]
B. \[\overrightarrow {DK} = \frac{1}{3}\left( {4\overrightarrow a – 2\overrightarrow b + \overrightarrow c } \right)\]
C. \[\overrightarrow {DK} = 4\overrightarrow a – 2\overrightarrow b + \overrightarrow c \]
D. \[\overrightarrow {DK} = 4\overrightarrow a – 2\overrightarrow b + 3\overrightarrow c \]
Lời giải
Chọn A

Vì I là trung điểm của \[B’C’ \Rightarrow \overrightarrow {A’B’} + \overrightarrow {A’C’} = 2\overrightarrow {A’I} \]
Và K là giao điểm của A’I, B’D’ nên t
heo định lí Talet Þ \[\overrightarrow {A’K} = \frac{2}{3}\overrightarrow {A’I} \]
Ta có
\[\begin{array}{l}\overrightarrow {A’K} = \overrightarrow {AA’} + \overrightarrow {A’K} = \overrightarrow {AA’} + \frac{2}{3}\overrightarrow {A’I} \\ = \overrightarrow {AA’} + \frac{1}{3}\left( {\overrightarrow {A’B’} + \overrightarrow {A’C’} } \right)\\ = \frac{1}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b + \overrightarrow c \end{array}\]
Khi đó
\[\begin{array}{l}\overrightarrow {DK} = \overrightarrow {DA} + \overrightarrow {AK} = \overrightarrow {CB} + \overrightarrow {AK} \\ = \left( {\overrightarrow {AB} – \overrightarrow {AC} } \right) + \overrightarrow {AK} \end{array}\]
\[ = \overrightarrow a – \overrightarrow b + \frac{1}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b + \overrightarrow c = \frac{4}{3}\overrightarrow a – \frac{2}{3}\overrightarrow b + \overrightarrow c \]
Câu 6: Cho tứ diện ABCD có trọng tâm G. Mệnh đề nào sau đây là sai?
A. \[\overrightarrow {AG} = \frac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\]
B. \[\overrightarrow {AG} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} } \right)\]
C. \[\overrightarrow {OG} = \frac{1}{4}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right)\]
D. \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \]
Lời giải
Chọn A
Xem thêm