Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Chuyên đề về góc và khoảng cách trong không gian
GÓC – KHOẢNG CÁCH
§1. Các dạng toán liên quan đến tính Góc
1. 1 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm và lần lượt song song với a và b.
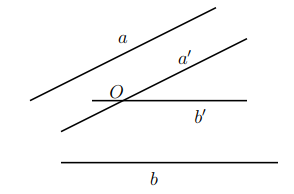
Để xác định góc giữa hai đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.
Nếu \[\overrightarrow u \] và \[\overrightarrow v \] lần lượt là vec-tơ chỉ phương của a và b, đồng thời \[\left( {\overrightarrow u ,\overrightarrow v } \right) = \alpha \] thì góc giữa hai đường thẳng a và b bằng α nếu 00 ≤ α ≤ 900 và bằng 1800 − α nếu 900 < α ≤ 1800.
Nếu a và b là hai đường thẳng song song hoặc trùng nhau thì góc giữa chúng bằng 00.
Xác định góc giữa hai đường thẳng trong không gian. Ta thường có hai phương pháp để giải quyết cho dạng toán này.
Phương pháp 1: Sử dụng định nghĩa góc giữa hai đường thẳng, kết hợp sử dụng hệ thức lượng trong tam giác (định lý cos, công thức trung tuyến).
Phương pháp 2: Sử dụng tích vô hương của hai vec-tơ.
Ví dụ 1.
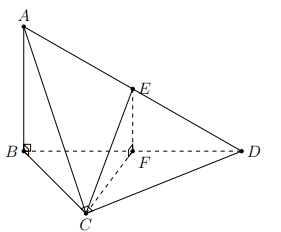
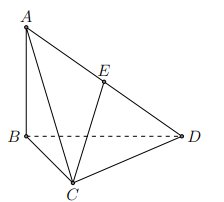
Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \[AB = \frac{{a\sqrt 6 }}{2},AC = a\sqrt 2 ,CD = a\]. Gọi E là trung điểm của AC (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AB và DE bằng
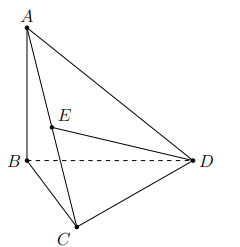
A. 450.
B. 600.
C. 300.
D. 900.
Hướng dẫn giải:
Gọi I là trung điểm của BC, suy ra EI // AB.
Khi đó \[(AB,DE) = (EI,ED) = \widehat {IED}\]
Ta có \[\left\{ {\begin{array}{*{20}{c}}{DC \bot BC(giathiet)}\\{DC \bot AB(AB \bot (BCD))}\end{array}} \right. \Rightarrow DC \bot (ABC)\]
suy ra DC vuông góc với EC. Do đó
\[\begin{array}{l}D{E^2} = C{D^2} + E{C^2} = C{D^2} + \frac{{A{C^2}}}{4} = \frac{{3{a^2}}}{2}\\ \Rightarrow DE = \frac{{a\sqrt 6 }}{2}\end{array}\]
Ta có \[IE = \frac{{AB}}{2} = \frac{{a\sqrt 6 }}{4}\] và \[B{C^2} = A{C^2} – A{B^2} = \frac{{{a^2}}}{2}\].
Tam giác ICD vuông tại C nên
\[D{I^2} = C{D^2} + I{C^2} = C{D^2} + \frac{{B{C^2}}}{4} = \frac{{9{a^2}}}{8}\].
Áp dụng định lý cô-sin cho tam giác IDE, ta có:
\[\begin{array}{l}\cos \widehat {IED} = \frac{{I{E^2} + D{E^2} – C{D^2}}}{{2IE.DE}} = \frac{{\frac{{3{a^2}}}{8} + \frac{{3{a^2}}}{2} – \frac{{9{a^2}}}{8}}}{{2.\frac{{a\sqrt 6 }}{4}.\frac{{a\sqrt 6 }}{2}}} = \frac{1}{2}\\ \Rightarrow \widehat {IED} = {60^0}\end{array}\]
Vậy góc giữa hai đường thẳng AB và DE bằng 600.
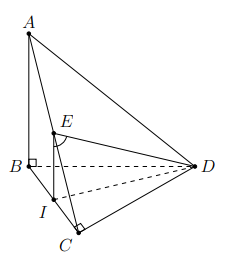
Có thể chứng minh EI vuông góc với mặt phẳng (BCD), suy ra tam giác EID vuông tại I để tính góc \[\widehat {IED}\] đơn giản hơn mà không cần sử dụng định lý cô-sin.
Ví dụ 2. Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \[AB = \frac{{a\sqrt 6 }}{2},AC = a\sqrt 2 ,CD = a\]. Gọi E là trung điểm của AD (tham khảo hình vẽ dưới đây).
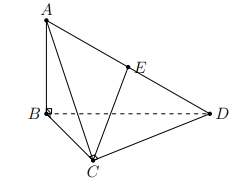
Góc giữa hai đường thẳng AB và CE bằng
A. 600.
B. 450.
C. 300.
D. 900.
Hướng dẫn giải:
Gọi F là trung điểm của BD, suy ra EF // AB nên (AB, CE) = (EF, CE).
Do AB ⊥ (BCD) nên EF ⊥ (BCD), suy ra \[\Delta EFC\] vuông tại F.
Mặt khác \[\left\{ {\begin{array}{*{20}{c}}{CD \bot BC}\\{CD \bot AB}\end{array}} \right. \Rightarrow CD \bot AC\].
Ta có \[EF = \frac{1}{2}AB = \frac{{a\sqrt 6 }}{4},AD = \sqrt {A{C^2} + C{D^2}} = a\sqrt 3 \].
\[\Delta ACD\]vuông tại C và có E là trung điểm của AD nên
\[CE = \frac{1}{2}AD = \frac{{a\sqrt 3 }}{2}\] .
\[\cos \widehat {CEF} = \frac{{EF}}{{EC}} = \frac{{\sqrt 2 }}{2} \Rightarrow \widehat {CEF} = {45^0}\].
Vậy (AB, CE) = (EF, CE) = \[\widehat {CEF} = {45^0}\].
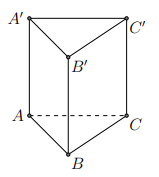
Ví dụ 3. Cho hình lăng trụ đứng tam giác \[ABC.A’B’C’\] có đáy ABC là tam giác cân AB = AC = a, \[\widehat {BAC} = {120^0}\], cạnh bên \[AA’ = a\sqrt 2 \]. Tính góc giữa hai đường thẳng \[AB’\]và BC (tham khảo hình vẽ bên).
A. 900.
B. 300.
C. 450.
D. 600.
Hướng dẫn giải:
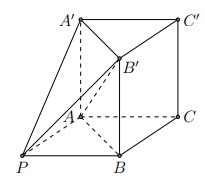
Dựng AP sao cho song song và bằng với CB như hình vẽ.
Suy ra (BC, AB’) = (AP, AB’).
Ta có AP = CB = \[a\sqrt 3 \].
Ta lại có \[AB’ = \sqrt {B'{B^2} + A{B^2}} = a\sqrt 3 \];
\[B’P = \sqrt {B'{B^2} + P{B^2}} = a\sqrt 3 \].
Vậy \[\Delta APB’\]đều nên (BC,AB’) = (AP,AB’) = 600.
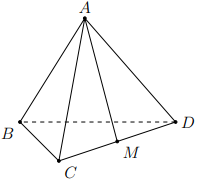
Ví dụ 4. Cho tứ diện đều ABCD có M là trung điểm của cạnh CD (tham khảo hình vẽ), \[\varphi \] là góc giữa hai đường thẳng AM và BC. Giá trị cos \[\varphi \] bằng
A. \[\frac{{\sqrt 3 }}{6}\].
B. \[\frac{{\sqrt 3 }}{4}\].
C. \[\frac{{\sqrt 2 }}{3}\].
D. \[\frac{{\sqrt 2 }}{6}\].
Hướng dẫn giải:
Giả sử cạnh của tứ diện đều bằng a.
Ta có:
\[\overrightarrow {CB} .\overrightarrow {AM} = \overrightarrow {CB} (\overrightarrow {CM} – \overrightarrow {CA} ) = \overrightarrow {CB} .\overrightarrow {CM} – \overrightarrow {CB} .\overrightarrow {CA} \]
= \[CB.CM.\cos \widehat {ACM} – CB.CA.\cos \widehat {ACB} = – \frac{{{a^2}}}{4}\]
\[\cos \varphi = \left| {\cos \left( {\overrightarrow {BC} ,\overrightarrow {AM} } \right)} \right| = \left| {\frac{{\overrightarrow {BC} .\overrightarrow {AM} }}{{BC.AM}}} \right| = \frac{{\sqrt 3 }}{6}\]
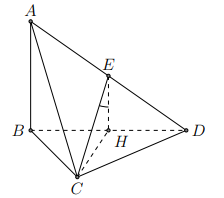
Ví dụ 5. Cho tứ diện ABCD có AB vuông góc với mặt phẳng (BCD). Biết tam giác BCD vuông tại C và \[AB = \frac{{a\sqrt 6 }}{2}\], \[AC = a\sqrt 2 \], CD = a. Gọi E là trung điểm của AD (tham khảo hình vẽ bên). Góc giữa hai đường thẳng AB và CE bằng
A. 450.
B. 600.
C. 300.
D. 900.
Hướng dẫn giải:
Gọi H là trung điểm của BD.
Khi đó EH // AB và EH ⊥ (BCD). Góc giữa AB và CE bằng góc giữa EH và EC và bằng \[\widehat {HEC}\]
Ta có \[EH = \frac{1}{2},AB = \frac{{a\sqrt 6 }}{4}\], \[BC = \sqrt {A{C^2} – A{B^2}} = \frac{{a\sqrt 2 }}{2}\],
\[\begin{array}{l}C{H^2} = \frac{{2(C{B^2} + C{D^2}) – B{D^2}}}{4} = \frac{{3{a^2}}}{8}\\ \Rightarrow CH = \frac{{a\sqrt 6 }}{4}\end{array}\].
Vì\[\tan \widehat {HEC} = \frac{{CH}}{{EH}} = \frac{{a\sqrt 6 }}{4} \div \frac{{a\sqrt 6 }}{4} = 1\]nên \[\widehat {HEC} = {45^0}\].
Vậy góc giữa AB và CE bằng 450.
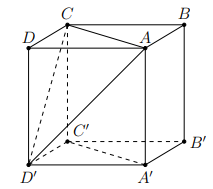
Ví dụ 6. Cho hình lập phương \[ABCD.A’B’C’D’\]. Góc giữa \[AC’\] và \[D’C\] là
A. 1200.
B. 450.
C. 600.
D. 900.
Hướng dẫn giải:
Ta có \[A’C’//AC\] nên \[(A’C’,D’C) = (D’C,AC)\]
Dễ thấy tam giác ACD’ là tam giác đều nên \[\widehat {D’CA} = {60^0}\], do đó
\[(A’C’,D’C) = (D’C,AC) = {60^0}\].
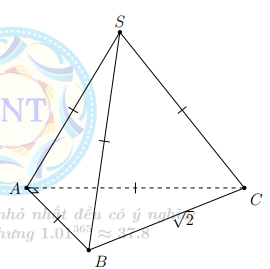
Ví dụ 7. Cho hình chóp S.ABC có SA = SB = SC = AB = AC = 1, BC = \[\sqrt 2 \]. Tính góc giữa hai đường thẳng AB, SC.
A. 450.
B. 1200.
C. 300.
D. 600.
Hướng dẫn giải:
Ta có AB2 + AC2 = 2 = BC2 ⇒ ∆ABC vuông tại A.
\[\cos \left( {\overrightarrow {AB} ,\overrightarrow {SC} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {SC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {SC} } \right|}} = \frac{{\overrightarrow {AB} .\left( {\overrightarrow {AC} – \overrightarrow {AS} } \right)}}{{1.1}}\]
\[ = \overrightarrow {AB} \overrightarrow {AC} – \overrightarrow {AB} \overrightarrow {AS} \]\[ = 0 – 1.1.\cos {60^0}\]\[ = – \frac{1}{2}\]
Suy ra \[\left( {\overrightarrow {AB} ,\overrightarrow {SC} } \right) = {120^0}\].
Do đó góc giữa hai đường thẳng AB và SC bằng 1800 – 1200 = 600.
Xem thêm