Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Phương trình đường thẳng
Phương trình đường tròn
Elip
Ôn tập chương III
Tài liệu phương pháp tọa độ trong mặt phẳng
Chương III
Phương pháp tọa độ trong mặt phẳng
Ôn tập tọa độ trong mặt phẳng
1. Hệ trục tọa độ Oxy gồm hai trục Ox, Oy đôi một vuông góc với nhau với hai vectơ đơn vị \(\vec i,\vec j\) \((|\vec i| = |\vec j| = 1)\). Gọi là hệ trục tọa độ \((O,\vec i,\vec j)\) hay gọi mặt phẳng (Oxy)
2. Tọa độ của vecto và của điểm:
\(\begin{array}{l}\vec a = \left( {{a_1};{a_2}} \right) \Leftrightarrow \vec a = {a_1}\vec i + {a_2}\vec j;\\M(x;y) \Leftrightarrow \overrightarrow {OM} = x\vec i + y\vec j\end{array}\)
3. Biểu thức tọa độ của vecto: Cho \(\vec u = (x;y),\vec v = \left( {{x^\prime };{y^\prime }} \right)\)
a. \(\vec u = \vec v \Leftrightarrow \left( {x = {x^\prime };y = {y^\prime }} \right)\)
b. \(\vec u \pm \vec v = \left( {x \pm {x^\prime };y \pm {y^\prime }} \right)\)
c. \(k\vec u = (kx;ky)\)
d. \(\vec u \cdot \vec v = x{x^\prime } + y{y^\prime }\)
e. \(\vec u \bot \vec v \Leftrightarrow x{x^\prime } + y{y^\prime } = 0\)
f. \(|\vec u| = \sqrt {{x^2} + {y^2}} \)
g. \(\cos (\vec u,\vec v) = \frac{{\vec u \cdot \vec v}}{{|\vec u| \cdot |\vec v|}} = \frac{{x \cdot {x^\prime } + y \cdot {y^\prime }}}{{\sqrt {{x^2} + {y^2}} \cdot \sqrt {{x^{\prime 2}} + {y^{\prime 2}}} }}\).
4. Liên hệ giữa tọa độ điểm và vecto : Cho \(A\left( {{x_{\rm{A}}};{y_{\rm{A}}}} \right),B\left( {{x_{\rm{B}}};{y_{\rm{B}}}} \right)\)
a. \(\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A}} \right)\)
b. \(|\overrightarrow {AB} | = AB = \sqrt {{{\left( {{x_B} – {x_A}} \right)}^2} + {{\left( {{y_B} – {y_A}} \right)}^2}} \)
c. G là trọng tâm tam giác ABC ta có: \({x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3};{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\)
d. M chia AB theo tỉ số \(k:{x_M} = \frac{{{x_A} – k{x_B}}}{{1 – k}};{y_M} = \frac{{{y_A} – k{y_B}}}{{1 – k}}\)
Đặc biệt M là trung điểm của \(AB:{x_M} = \frac{{{x_A} + {x_B}}}{2};{y_M} = \frac{{{y_A} + {y_B}}}{2}\).
§1. Phương trình đường thẳng
A. Kiến thức cần nắm
I. Vecto chỉ phương và vecto pháp tuyến của đường thẳng
1. Vecto chỉ phương của đường thẳng (VTCP)
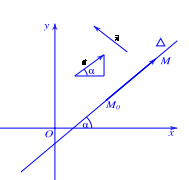
a. Định nghĩa: Vectơ \(\vec u\) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu \(\vec u \ne \vec 0\) và giá của \(\vec u\) song song hoặc trùng với \(\Delta \).
b. Nhận xét
– Nếu \(\vec u\) là một VTCP của đường thẳng \(\Delta \) thì \(k\vec u(k \ne 0)\) cũng là một VTCP của \(\Delta \). Do đó một đường thẳng có vô số VTCP.
– Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một VTCP của đường thẳng đó.
2. Vecto pháp tuyến của đường thẳng (VTPT)
a. Định nghĩa: Vectơ \(\vec n\) được gọi là VTPT của đường thẳng \(\Delta \) nếu \(\vec n \ne \vec 0\) và \(\vec n\) vuông góc với VTCP của \(\Delta \).
b. Nhận xét
– Nếu \(\vec n\) là một VTPT của đường thẳng \(\Delta \) thì \(k\vec n(k \ne 0)\) cũng là một VTPT của \(\Delta \). Do đó một đường thẳng có vô số VTPT.
– Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một VTPT của đường thẳng đó.
3. Mối liên hệ giữa tọa độ VTCP và VTPT của đường thẳng
Gọi \(\vec u = (a;b)\) và \(\vec n = (A;B)\) lần lượt là VTCP và VTPT của đường thẳng \(\Delta \)
Ta có:
– \(\vec u \bot \vec n \Leftrightarrow \vec u \cdot \vec n = 0 \Leftrightarrow aA + bB = 0\)
– VTCP \(\vec u = (a;b)\) suy ra VTPT \(\vec n = (b; – a)\) hoặc \(\vec n = ( – b;a)\)
– VTPT \(\vec n = (A;B)\) suy ra VTCP \(\vec u = (B; – A)\) hoặc \(\vec u = ( – B;A)\)
– Đường thẳng \(\Delta \) có VTCP \(\vec u = (a;b)\) với \(a \ne 0\) thì \(\Delta \) có hệ số góc \(k = \tan \alpha = \frac{b}{a}\).
– Đường thẳng \(\Delta \) có hệ số góc \(k\) thì \(\Delta \) có VTCP \(\vec u = (1;k)\)
II. Phương trình đường thẳng
1. Phương trình tham số của đường thẳng (Ptts)
Đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{qua{M_0}\left( {{x_0};{y_0}} \right)}\\{VTCP\quad \vec u = (a;b)}\end{array}} \right.\).
Ptts của đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array},t \in \mathbb{R}} \right.\).
Luu ý:
– Cho t một giá trị cụ thể thì ta xác định được một điểm trên đường thẳng \(\Delta \)
– Nếu đường thẳng \(\Delta \) có phương trình \(\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array},t \in \mathbb{R}} \right.\). Suy ra đường thẳng \(\Delta \) đi qua điểm \({M_0}\left( {{x_0};{y_0}} \right)\) và có một VTCP là \(\vec u = (a;b)\).
2. Phương trình tổng quát của đường thẳng (Pttq)
Đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{{\rm{ qua }}{M_0}\left( {{x_0};{y_0}} \right)}\\{VTPT\vec n = (A;B),{A^2} + {B^2} \ne 0}\end{array}} \right.\).
Pttq của đường thẳng \(\Delta :A\left( {x – {x_0}} \right) + B\left( {y – {y_0}} \right) = 0 \Leftrightarrow Ax + By + C = 0\) ( với \(C = – A{x_0} – B{y_0}\) )
Luu ý: • Đường thẳng \(\Delta :Ax + By + C = 0\) thì \(\Delta \) có VTPT \(\vec n = (A;B)\)
3. Các trường hợp đặc biệt
Cho đường thẳng \(\Delta \) có phương trình tổng quát \(Ax + By + C = 0\) (1)
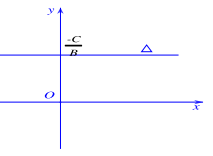
– \(A = 0,\) pt(1) trở thành: \(By + C = 0 \Leftrightarrow y = – \frac{C}{B}\). Khi đó đường thẳng \(\Delta \) vuông góc với trục Oy tại điểm \(\left( {0; – \frac{C}{B}} \right)\)
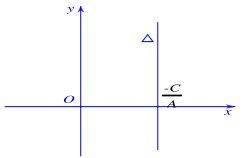
– \(B = 0,\) pt(1) trở thành: \(Ax + C = 0 \Leftrightarrow x = – \frac{C}{A}\). Khi đó đường thẳng \(\Delta \) vuông góc với trục Ox tại điểm \(\left( { – \frac{C}{A};0} \right)\)
– \(C = 0,\) pt(1) trở thành: \(Ax + By = 0\). Khi đó đường thẳng \(\Delta \) đi qua gốc tọa độ \(O\).
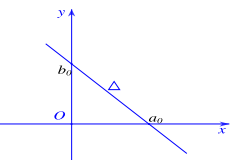
– Đường thẳng \(\Delta \) cắt các trục tọa độ tại \(M\left( {{a_0};0} \right),N\left( {0;{b_0}} \right)\). Phương trình đoạn chắn của \(\Delta \) là \(\frac{x}{{{a_0}}} + \frac{y}{{{b_0}}} = 1\).
– Đường thẳng \(\Delta \) đi qua \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Phương trình chính tắc của đường thẳng \(\Delta :\frac{{x – {x_A}}}{{{x_B} – {x_A}}} = \frac{{y – {y_A}}}{{{y_B} – {y_A}}}\). Khi \({x_B} – {x_A} = 0\) hoặc \({y_B} – {y_A} = 0\) thì đường thẳng không có phương trình chình tắc.
– Đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0}} \right)\) và có hệ số góc k có phương trình: \(y – {y_0} = k\left( {x – {x_0}} \right)\)
– Đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0}} \right)\) song song với đường thẳng \({\Delta _1}:{A_1}x + {B_1}y + {C_1} = 0\)
\( + \Delta //{\Delta _1} \Rightarrow \Delta :{A_1}x + {B_1}y + m = 0,\left( {m \ne {C_1}} \right)\)
+ Do \({M_0}\left( {{x_0};{y_0}} \right) \in \Delta \) nên \({A_1}{x_0} + {B_1}{y_0} + m = 0 \Rightarrow m = \) ? và kết luận.
– Đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0}} \right)\) vuông góc với đường thẳng \({\Delta _1}:{A_1}x + {B_1}y + {C_1} = 0\)
\( + \Delta \bot {\Delta _1} \Rightarrow \Delta :{B_1}x – {A_1}y + m = 0\) hay \[ – {B_1}x + {A_1}y + m = 0\]
+ Do \({M_0}\left( {{x_0};{y_0}} \right) \in \Delta \) nên \({B_1}{x_0} – {A_1}{y_0} + m = 0 \Rightarrow m = ?\) và kế luận.
III. Vị trí tương đối giữa hai đường thẳng
Cho hai đường thẳng \({\Delta _1}:{A_1}x + {B_1}y + {C_1} = 0\) và \({\Delta _2}:{A_2}x + {B_2}y + {C_2} = 0\)
Xét hệ phương trình \(\left\{ {\begin{array}{*{20}{l}}{{A_1}x + {B_1}y = – {C_1}}\\{{A_2}x + {B_2}y = – {C_2}}\end{array}(*)} \right.\)
– Hệ \((*)\) có một nghiệm \(\left( {{x_0};{y_0}} \right)\), khi đó \({\Delta _1}\) cắt \({\Delta _2}\) tại điểm \({M_0}\left( {{x_0};{y_0}} \right)\)
– Hệ \((*)\) có vô số nghiệm, khi đó \({\Delta _1}\) trùng với \({\Delta _2}\)
– Hệ (*) có vô nghiệm, khi đó \({\Delta _1} \cap {\Delta _2} = \emptyset \) hay \({\Delta _1}\) song song với \({\Delta _2}\)
Luu ý: Nếu \({A_2}{B_2}{C_2} \ne 0\) thì:
– \({\Delta _1}\) cắt \({\Delta _2} \Leftrightarrow \frac{{{A_1}}}{{{A_2}}} \ne \frac{{{B_1}}}{{{B_2}}}\)
– \({\Delta _1}//{\Delta _2} \Leftrightarrow \frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} \ne \frac{{{C_1}}}{{{C_2}}}\)
– \({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \frac{{{A_1}}}{{{A_2}}} = \frac{{{B_1}}}{{{B_2}}} = \frac{{{C_1}}}{{{C_2}}}\)
IV. Góc giữa hai đường thẳng
Cho hai đường thẳng \({\Delta _1}:{A_1}x + {B_1}y + {C_1} = 0\) và \({\Delta _2}:{A_2}x + {B_2}y + {C_2} = 0\). Đặt \(\varphi = \left( {\widehat {{\Delta _1},{\Delta _2}}} \right)\)
–
– \({\Delta _1}{\not \not \Delta _2}.\)
+ Xác định hai VTPT \({\vec n_1},{\vec n_2}\) (hay VTCP) của hai đường thẳng \({\Delta _1},{\Delta _2}\)
+ Tính \(\cos \varphi = \left| {\cos \left( {{{\vec n}_1},{{\vec n}_2}} \right)} \right| = \frac{{\left| {{{\vec n}_1} \cdot {{\vec n}_2}} \right|}}{{\left| {{{\vec n}_1}} \right| \cdot \left| {{{\vec n}_2}} \right|}}\). Suy ra góc \(\varphi = \) ?
Chú ý: Nếu \({\Delta _1}\) và \({\Delta _2}\) có phương trình \(y = {k_1}x + {m_1}\) và \(y = {k_2}x + {m_2}\) thì
\(\begin{array}{l} – {\Delta _1}//{\Delta _2} \Rightarrow {k_1} = {k_2}\quad \\ – {\Delta _1} \bot {\Delta _2} \Rightarrow {k_1} \cdot {k_2} = – 1\end{array}\)
V. Khoảng cách từ một điểm đến một đường thẳng
Cho đường thẳng \(\Delta :Ax + By + C = 0\) và điểm \({M_0}\left( {{x_0};{y_0}} \right)\). Khoảng cách từ điểm \({M_0}\) đền đường thẳng \(\Delta \),kí hiệu là \(d\left( {{M_0},\Delta } \right)\) và được tính bởi công thức: \(d\left( {{M_0},\Delta } \right) = \frac{{\left| {A{x_0} + B{y_0} + C} \right|}}{{\sqrt {{A^2} + {B^2}} }}\)
VI. Phương trình hai đường phân giác của các góc tạo bởi : \({\Delta _1}:{A_1}x + {B_1}y + {C_1} = 0\);
\({\Delta _2}:{A_2}x + {B_2}y + {C_2} = 0\) là: \(\frac{{{A_1}x + {B_1}y + {C_1}}}{{\sqrt {A_1^2} + B_1^2}} = \pm \frac{{{A_2}x + {B_2}y + {C_2}}}{{\sqrt {A_2^2 + B_2^2} }}\)
Lưu ý: Dấu \( \pm \) tương ứng vớ 1 đường phân giác của góc nhọn và 1 đường phân giác góc tù. Để phân biệt được dấu nào là của đường phân giác góc nhọn và dấu nào là đường phân giác góc tù thì cần nhó quy tắc sau:
Đường phân giác góc nhọn luôn nghịch dấu với tích hai pháp véctơ, đường phân giác góc tù mang dấu còn lại.
VII. Cho hai điểm \(M\left( {{x_M};{y_M}} \right),N\left( {{x_N};{y_N}} \right)\) và đường thẳng \(\Delta :Ax + By + C = 0\). Khi đó:
– M và N nằm cùng phía đối với \(\Delta \Leftrightarrow \left( {A{x_M} + B{y_M} + C} \right)\left( {A{x_N} + B{y_N} + C} \right) > 0\)
– M và N nằm khác phía đối với \(\Delta \Leftrightarrow \left( {A{x_M} + B{y_M} + C} \right)\left( {A{x_N} + B{y_N} + C} \right) < 0\)
B. Bài tập
Các bài tập dưới đây, xét trong mặt phẳng Oxy.
Vấn đề 1. Viết phương trình đường thẳng
1. Đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{qua{M_0}\left( {{x_0};{y_0}} \right)}\\{VTCP{\rm{ u }} = (a;b)}\end{array}} \right.\). Ptts của đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = {x_0} + at}\\{y = {y_0} + bt}\end{array},t \in \mathbb{R}} \right.\).
2. Đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{{\rm{ qua }}{M_0}\left( {{x_0};{y_0}} \right)}\\{VTPT\vec n = (A;B),{A^2} + {B^2} \ne 0}\end{array}} \right.\).
Pttq của đường thẳng \(\Delta :A\left( {x – {x_0}} \right) + B\left( {y – {y_0}} \right) = 0 \Leftrightarrow Ax + By + C = 0\) (với \(C = – A{x_0} – B{y_0}\) )
3. Đường thẳng \(\Delta \) cắt các trục tọa độ tại \(M\left( {{a_0};0} \right),N\left( {0;{b_0}} \right)\). Phương trình đoạn chắn của \(\Delta \) là \(\frac{x}{{{a_0}}} + \frac{y}{{{b_0}}} = 1\).
4. Đường thẳng \(\Delta \) đi qua \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Phương trình chính tắc của đường thẳng \(\Delta :\frac{{x – {x_A}}}{{{x_B} – {x_A}}} = \frac{{y – {y_A}}}{{{y_B} – {y_A}}}\). Khi \({x_B} – {x_A} = 0\) hoặc \({y_B} – {y_A} = 0\) thì đường thẳng không có phương trình chình tắc.
5. Đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0}} \right)\) và có hệ số góc k có phương trình: \(y – {y_0} = k\left( {x – {x_0}} \right)\) Lưu ý : Đường thẳng \(\Delta \) có hệ số góc k thì \(\Delta \) có VTCP \(\vec u = (1;k)\)
6. Đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0}} \right)\) song song với đường thẳng \({\Delta _1}:{A_1}x + {B_1}y + {C_1} = 0\)
\( + \Delta //{\Delta _1} \Rightarrow \Delta :{A_1}x + {B_1}y + m = 0,\left( {m \ne {C_1}} \right)\)
+ Do \({M_0}\left( {{x_0};{y_0}} \right) \in \Delta \) nên \({A_1}{x_0} + {B_1}{y_0} + m = 0 \Rightarrow m = \) ? và kết luận.
7. Đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0}} \right)\) vuông góc với đường thẳng \({\Delta _1}:{A_1}x + {B_1}y + {C_1} = 0\)
\( + \Delta \bot {\Delta _1} \Rightarrow \Delta :{B_1}x – {A_1}y + m = 0\) hay \( – {B_1}x + {A_1}y + m = 0\)
+ Do \({M_0}\left( {{x_0};{y_0}} \right) \in \Delta \) nên \({B_1}{x_0} – {A_1}{y_0} + m = 0 \Rightarrow m = \) ? và kết luận.
Bài 1.1. Lập phương trình tham số của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a. \(\Delta \) đi qua điểm \(M(2;1)\) và có VTCP \(\vec u = (3;4)\).
b. \(\Delta \) đi qua điểm \(P(5; – 2)\) và có VTPT \(\vec n = (4; – 3)\).
c. \(\Delta \) đi qua điểm \(Q(5;1)\) và có hệ số góc \(k = 3\).
d. \(\Delta \) đi qua hai điểm \(A(3;4)\) và \(B(4;2)\).
Hướng dẫn giải
a. Ta có đường thẳng
Ptts của \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 2 + 3t}\\{y = 1 + 4t}\end{array},t \in \mathbb{R}} \right.\).
b. Ta có đường thẳng
Ptts của \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 5 + 3t}\\{y = – 2 + 4t}\end{array},t \in \mathbb{R}} \right.\).
d. Ta có đường thẳng \(\Delta \) : \(\left\{ {\begin{array}{*{20}{l}}{{\rm{ di qua }}A(3;4)}\\{VTCP\overrightarrow {AB} = (1; – 2)}\end{array}} \right.\).
Ptts của \(\Delta :\left\{ {\begin{array}{*{20}{l}}{x = 3 + t}\\{y = 4 – 2t}\end{array},t \in \mathbb{R}} \right.\).
Bài 1.2. Lập phương trình tổng quát của đường thẳng \(\Delta \) trong mỗi trường hợp sau:
a. \(\Delta \) đi qua điểm \(M(3;4)\) và có VTPT \(\vec n = (1;2)\).
b. \(\Delta \) đi qua điểm \(P(3; – 2)\) và có VTCP \(\vec u = (4;3)\)
c. \(\Delta \) đi qua điểm \(Q( – 5; – 8)\) và có hệ số góc \(k = – 3\).
d. \(\Delta \) đi qua hai điểm \(A(2;1)\) và \(B( – 4;5)\).
e. \(\Delta \) qua \(C( – 1;1)\) và vuông góc với đường thẳng có phương trình \({\Delta _1}:2x – 3y + 1 = 0\).
f. \(\Delta \) qua \(D(2;0)\) và song song với đường thẳng có phương trình \({\Delta _2}:2x + y – 5 = 0\).
HD Giải
a. Ta có đường thẳng . Pttq của \(\Delta :1(x – 3) + 2(y – 4) = 0 \Leftrightarrow x + 2y – 11 = 0\)
b. Ta có đường thẳng
Pttq của \(\Delta :3(x – 3) – 4(y + 2) = 0 \Leftrightarrow 3x – 4y – 17 = 0\).
c. Ta có đường thẳng
\(\begin{array}{l} \Rightarrow VTCP\,\vec u = (1; – 3)\\ \Rightarrow VTPT\,\vec n = (3;1)\end{array}\)
Pttq của \(\Delta :3(x + 5) + y + 8 = 0 \Leftrightarrow 3x + y + 23 = 0\)
Chú ý:
– Ta có đường thẳng \(\Delta :\left\{ {\begin{array}{*{20}{l}}{{\rm{ di qua }}Q( – 5; – 8)}\\{{\rm{ c\’o he so g\’o c }}k = – 3}\end{array}} \right.\).
Pttq của \(\Delta :y + 8 = – 3(x + 5) \Leftrightarrow 3x + y + 23 = 0\)
Từ đó, ta có phương trình: \(\frac{{x + 5}}{1} = \frac{{y + 8}}{{ – 3}} \Leftrightarrow 3x + y + 23 = 0\).
\({\rm{d}}\). Ta có đường thẳng \(\Delta \) : \(\left\{ {\begin{array}{*{20}{l}}{{\rm{ di qua }}A(2;1)}\\{VTCP\overrightarrow {AB} = ( – 6;4) \Rightarrow VTPT\vec n = (4;6)}\end{array}} \right.\).
Pttq của \(\Delta :4(x – 2) + 6(y – 1) = 0\)
\( \Leftrightarrow 4x + 6y – 14 = 0\) hay \(2x + 3y – 7 = 0\)
Chú ý: Ta có \(\Delta \) đi qua hai điểm \(A(2;1)\) và \(B( – 4;5)\) có \({\rm{pt}}:\frac{{x – 2}}{{ – 4 – 2}} = \frac{{y – 1}}{{5 – 1}} \Leftrightarrow 2x + 3y – 7 = 0\)
e. Ta có \(\Delta \bot {\Delta _1} \Rightarrow \Delta :3x + 2y + m = 0\).
Do \(C( – 1;1) \in \Delta \) nên \(3( – 1) + 2.1 + m = 0 \Leftrightarrow m = 1\). Vậy pt của \(\Delta :3x + 2y + 1 = 0\).
f. Ta có \(\Delta //{\Delta _2} \Rightarrow \Delta :2x + y + m = 0,(m \ne – 5)\).
Do \(D(2;0) \in \Delta \) nên \(2.2 + 1.0 + m = 0 \Leftrightarrow m = – 4\). Vậy pt của \(\Delta :2x + y – 4 = 0\).
Bài 1.3. Cho tam giác ABC, biết \(A(1;4),B(3; – 1)\) và \(C(6;2)\).
a. Lập phương trình các cạnh của tam giác ABC.
b. Lập phương trình đường cao AH và đường trung tuyến AM.
HD Giải
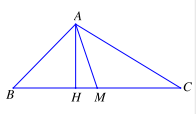
Áp dụng: Đường thẳng \(\Delta \) đi qua \(A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right)\). Phương trình
chính tắc của đường thẳng \(\Delta :\frac{{x – {x_A}}}{{{x_B} – {x_A}}} = \frac{{y – {y_A}}}{{{y_B} – {y_A}}}\).
a. Phương trình đường thẳng \(AB:\frac{{x – 1}}{{3 – 1}} = \frac{{y – 4}}{{ – 1 – 4}} \Leftrightarrow 5x + 2y – 13 = 0\)
Phương trình đường thẳng \(AC:\frac{{x – 1}}{{6 – 1}} = \frac{{y – 4}}{{2 – 4}} \Leftrightarrow 2x + 5y – 22 = 0\)
Phương trình đường thẳng \(BC:\frac{{x – 3}}{{6 – 3}} = \frac{{y + 1}}{{2 – ( – 1)}} \Leftrightarrow x – y – 4 = 0\)
b. Phương trình đường cao AH.
Ta có \(AH \bot BC \Rightarrow AH:x + y + m = 0\). Do \(A \in AH\) nên: \(1 + 4 + m = 0 \Leftrightarrow m = – 5\)
Vậy: \(AH:x + y – 5 = 0\)
Xem thêm