Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Dấu nhị thức bậc nhất
Tam thức bậc hai
Bài tập
Dấu của đa thức bậc nhất và bậc hai trong chương trình lớp 10
Chương 1
Dấu của đa thức
1.1 Dấu nhị thức bậc nhất
Định nghĩa 1.1. Nhị thức bạcc nhất theo biến x là biểu thức có dạng f(x) = ax +b \((a \ne 0)\).
Định lí 1.1. Dấu f(x) = ax +b cùng dấu a nếu \(x > – \frac{b}{a}\) và trái dấu a nếu \(x < \frac{b}{a}\)
Ví dụ 1.1. Xét dấu nhị thức f(x) = x – 2.
Lời giải. Nghiệm của f(x) là x = 2.
Bảng xét dấu.
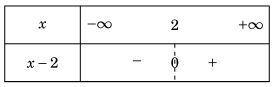
Từ bảng xét dấu, ta có
– \(f(x) > 0 \Leftrightarrow x \in (2, + \infty )\);
– \(f(x) < 0 \Leftrightarrow x \in ( – \infty ,2)\).
Ví dụ 1.2. Xét dấu nhị thức \(f(x) = 3 – 4x\).
Lời giải. Nghiệm của f(x) là \(x = \frac{3}{4}\). Hệ số của x là -4.
Bảng xét dấu.
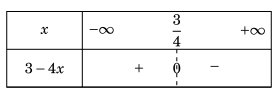
Từ bảng xét dấu, ta có
– \(f(x) > 0 \Leftrightarrow x \in \left( { – \infty ,\frac{3}{4}} \right)\)
– \(f(x) < 0 \Leftrightarrow x \in \left( {\frac{3}{4}, + \infty } \right)\).
1.1.1 Dấu tích các nhị thức bậc nhất
Ví du 1.3. Xét dấu \(f(x) = (x – 2)(3 – x)\).
Lời giải. Nghiệm của f(x) là x=2 và x=3.
Bảng xét dấu.
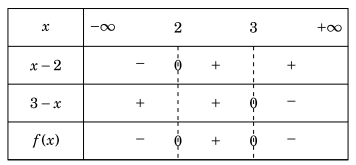
Ví dụ 1.4. Xét dấu của \(f(x) = (x + 2)\left( {{x^2} + 5x + 6} \right)\).
Lời giải. \(f(x) = {(x + 2)^2}(x + 3)\). Nghiệm của f(x) là \(x = – 2\) và \(x = – 3\).
Chú ý là với mọi x.
Bảng xét dấu.
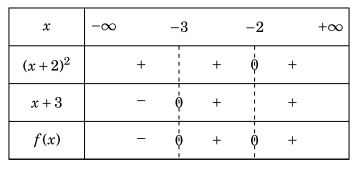
Từ bảng xét dấu, ta có
\(f(x) < 0 \Leftrightarrow x \in ( – \infty , – 3);f(x) > 0 \Leftrightarrow x \in ( – 3, + \infty )\backslash \{ – 2\} \).
1.1.2 Dấu thương các nhị thức bậc nhất
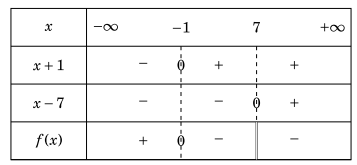
Ví dụ 1.5. Xét dấu \(f(x) = \frac{{x + 1}}{{x – 7}}\).
Lời giải. f(x) = 0 với x= -1 và f(x) không xác định tại x=7.
Bảng xét dấu.
Ví dụ 1.6. Xét dấu của \(f(x) = \frac{1}{{x + 2}} – \frac{3}{{x + 4}}\).
Lời giải.
Ta có
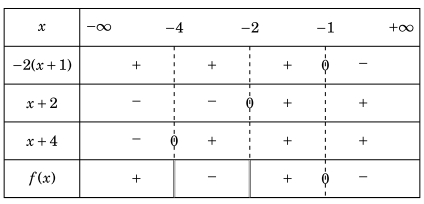
\(f(x) = – \frac{{2(x + 1)}}{{(x + 2)(x + 4)}}.\)
\(f(x) = 0\) tại \(x = – 1\) và \(f(x)\) không xác định tại \(x = – 2\) và \(x = – 4\).
Bảng xét dấu của \(f(x)\) như sau:
1.1.3 Ứng dụng xét dấu để giải bất phương trình
Ví dụ 1.7. Giải bất phương trình \((2x – 3)(4 – 5x) > 0\).
Lời giải. Đặt \(f(x) = (2x – 3)(5 – 4x)\).
Nhận thấy rằng \(f(x) = 0\) tại \(x = \frac{3}{2}\) hoặc \(x = \frac{5}{4}\).
Bảng xét dấu của f(x) như sau:
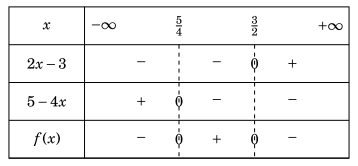
Dựa vào bảng xét dấu, tập nghiệm bất phương trình đã cho là \(\left( {\frac{5}{4},\frac{3}{2}} \right)\).
Ví dụ 1.8. Giải bất phương trình .
Ta có
Đặt \(f(x) = (x + 5)(3x + 1)\).
Nhận thây rằng \(f(x) = 0\) tại \(x = – 5\) hoặc \(x = – \frac{1}{3}\).
Bảng xét dấu của f(x) như sau:
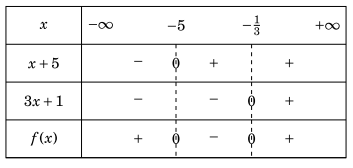
Dựa vào bảng xét dấu, tập nghiệm bất phương trình đã cho là \(( – \infty ; – 5] \cup \left[ { – \frac{1}{3}; + \infty } \right)\).
Ví dụ 1.9. Giải bất phương trình .
Lời giải. Ta có
Đặt \(f(x) = (x – 4)(x – 2)\). Bảng xét dâu của f(x) như sau:
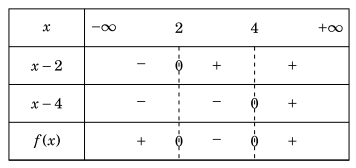
Ví dụ 1.10. Giải bất phương trình .
Lời giải. Điều kiện xác định của bât phương trình là .
Ta thấy x=4 là một nghiệm của bât phương trình đã cho.
Với \(x > 4\), thì \((x – 2)\sqrt {x – 4} > 0\), nên bất phương trình đã cho tương đương với hay
Vậy nghiệm bất phương trình đã cho là x = 4 hoặc .
Vi dụ 1.11.
Giải bât phương trình .
Lời giải. Điều kiện xác định của bât phương trình là .
Ta thây x = 4 là một nghiệm của bất phương trình đã cho.
Với \(x > 4\), từ bất phương trình đã cho, suy ra
\((x – 5)(9 – x) > 0 \Leftrightarrow 5 < x < 9.\)
Vậy nghiệm bất phương trình đã cho là x = 4 hoặc \(5 < x < 9\).
Ví dụ 1.12. Giải bất phương trình \(\frac{1}{x} > 1\).
Lời giải. Ta có
\(\frac{1}{x} > 1 \Leftrightarrow \frac{1}{x} – 1 > 0 \Leftrightarrow \frac{{1 – x}}{x} > 0\)
Đặt \(f(x) = \frac{{1 – x}}{x}\).
f(x)=0 tại x=1 và f(x) không xác định tại x=0.
Dựa vào bảng xét dấu, tập nghiệm bất phương trình đã cho là (0;1).
Lời bình. Không viết bất phương trình
\(\frac{1}{x} > 1 \Leftrightarrow 1 > x.\)
Vì ta chưa biết dấu của x.
Cũng có thể làm như sau: Nhận thây không là nghiệm của bất phương trình. Với x >0, bất phương trình tương đương với 1 > x.
Vậy nghiệm của bất phương trình là 0 < x < 1.
Xem thêm