Bài tập phương trình chứa căn

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài tập phương trình chứa căn

Dạng 1. Phương trình căn cơ bản

(1) \(\sqrt {\rm{A}}  = {\rm{B}} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{B}} \ge 0}\\{\;{\rm{A}} = {{\rm{B}}^2}}\end{array}} \right.\).

(2) \(\sqrt {\rm{A}}  = \sqrt {\rm{B}}  \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{\rm{B}} \ge 0}\\{\;{\rm{A}} = {\rm{B}}}\end{array}} \right.\).

Phương pháp tổng quát : (nếu không thuộc hai dạng trên)

– Bước 1. Đặt điều kiện cho căn có nghĩa.

– Bước 2. Chuyển vế sao cho hai vế không âm.

– Bước 3. Bình phương hai vế để đưa về một trong các dạng trên.

Bài tập áp dụng

Bài 1. Giải các phương trình

a/ \(\sqrt {2{\rm{x}} – 3}  = {\rm{x}} – 3\).

b/ \(\sqrt {5{\rm{x}} + 10}  = 8 – {\rm{x}}\)

c/ \({\rm{x}} – \sqrt {2{\rm{x}} – 5}  = 4\)

d/ \(\sqrt {{{\rm{x}}^2} + {\rm{x}} – 12}  = 8 – {\rm{x}}\).

e/ \(\sqrt {{\rm{x}} – 2}  = 4 – {\rm{x}}\)

f/ \(\sqrt {3{{\rm{x}}^2} – 9{\rm{x}} + 1}  = {\rm{x}} – 2\).

\(g/\sqrt {3{{\rm{x}}^2} – 9{\rm{x}} + 1}  = |{\rm{x}} – 2|\).

h) \(\sqrt {{{\rm{x}}^2} – 3{\rm{x}} – 10}  = {\rm{x}} – 2\)

i/ \({\rm{x}} – \sqrt {2{\rm{x}} + 7}  = 4\)

j/ \({\rm{x}} + \sqrt {{\rm{x}} – 1}  = 13\)

k/ \({\rm{x}} – \sqrt {{\rm{x}} – 1}  = 3\)

l/ \(\sqrt {{{\rm{x}}^2} – 3{\rm{x}} – 1}  = 2{\rm{x}} – 7\).

\({\rm{m}}/\sqrt {{{\rm{x}}^2} + 3{\rm{x}}}  = 3{\rm{x}} – 1\).

\({\rm{n}}/\sqrt {{{\rm{x}}^2} – 9{\rm{x}} + 1}  = {\rm{x}} – 2\).

o/ \(2{\rm{x}} – \sqrt {2{\rm{x}} – 1}  = 7\).

p/ \(\sqrt {3 – {\rm{x}}}  = 3{\rm{x}} – 5\).

q/ \(x – \sqrt {4{\rm{x}} – 3}  = 2\).

r/ \(\sqrt {{{\rm{x}}^2} – 1}  = {\rm{x}} – 1\)

s/ \({\rm{x}} – 2 = \sqrt {{{\rm{x}}^2} – 4{\rm{x}} + 3} \)

t/ \(\sqrt {{{\rm{x}}^2} – 3{\rm{x}} + 2}  = 2{\rm{x}} – 1\).

u/ \(\sqrt { – {{\rm{x}}^2} + 4{\rm{x}} – 3}  = 2{\rm{x}} – 5\).

v/ \(\sqrt {5 – {x^2}}  = x – 1\).

\({\rm{x}}/\sqrt {3{{\rm{x}}^2} + 5{\rm{x}} + 1}  + 1 = 4{\rm{x}}\).

\(y/\sqrt {{x^2} – 2x + 1}  = {x^2} – 2x + 1\).

Bài 2. Giải các phương trình

a/ \({{\rm{x}}^2} + \sqrt {{\rm{x}} + 7}  = 7\).

b/ \(\sqrt { – {{\rm{x}}^2} + 4{\rm{x}} – 3}  = 2{\rm{x}} – 5\).

c/ \(\sqrt {16{\rm{x}} + 17}  = 8{\rm{x}} – 23\).

d/ \(\sqrt { – {{\rm{x}}^2} + 4{\rm{x}}}  + 2 = 2{\rm{x}}\).

e/ \(\sqrt {{{\rm{x}}^2} – 6{\rm{x}} + 6}  = 2{\rm{x}} – 1\)

f/ \({{\rm{x}}^2} – 1 = \sqrt {{\rm{x}} + 1} \)

g/ \(\sqrt {4 – {{\rm{x}}^2}}  = {\rm{x}} + 2\).

h/ \(\sqrt {4 – {{\rm{x}}^2}}  = {\rm{x}} + 2\).

Bài 3. Giải các phương trình sau

a/ \(\sqrt {{{\rm{x}}^2} + 2{\rm{x}} + 4}  = \sqrt {2 – {\rm{x}}} \).

b/ \(\sqrt {{{\rm{x}}^2} – 3{\rm{x}}}  = \sqrt {2{\rm{x}} – 1} .\)

c/ \(\sqrt {2{{\rm{x}}^2} – 2{\rm{x}} + 4}  = \sqrt {{{\rm{x}}^2} – {\rm{x}} + 2} \).

d/ \(\sqrt {{{\rm{x}}^2} – 3{\rm{x}} – 2}  = \sqrt {{\rm{x}} – 3} \).

Bài 4. Giải các phương trình sau

a/ \(\sqrt {2{\rm{x}} + 1}  = 2 + \sqrt {{\rm{x}} – 3} \).

b/ \(\sqrt {3{\rm{x}} + 4}  – \sqrt {{\rm{x}} – 3}  = 3\).

cl \(\sqrt {{\rm{x}} – 3}  – \sqrt {{\rm{x}} + 2}  = 5\).

d/ \(\sqrt {2{\rm{x}} + 1}  = 4 – \sqrt {{\rm{x}} – 3} \).

e/ \(\sqrt {5{\rm{x}} – 1}  = \sqrt {3{\rm{x}} – 2}  + \sqrt {2{\rm{x}} + 2} .\quad \)

f/ \(\quad \sqrt {3{\rm{x}} + 1}  – \sqrt {4{\rm{x}} – 3}  = \sqrt {5{\rm{x}} + 4} \)

g/ \(\sqrt {{\rm{x}} + 1}  – \sqrt {{\rm{x}} – 1}  = 1\)

\({\rm{h}}/\sqrt {3{\rm{x}} + 7}  – \sqrt {{\rm{x}} + 1}  = 2\).

i/ \(\sqrt {{{\rm{x}}^2} + 9}  – \sqrt {{{\rm{x}}^2} – 7}  = 2\).

j/ \(\sqrt {3{{\rm{x}}^2} + 5{\rm{x}} + 8}  – \sqrt {3{{\rm{x}}^2} + 5{\rm{x}} + 1}  = 1\).

\({\rm{k}}/\sqrt {2{\rm{x}} + 3}  + \sqrt {2{\rm{x}} + 2}  = 1\).

1/ \(\sqrt {{\rm{x}} + 4}  – \sqrt {2{\rm{x}} – 6}  = 1\)

\({\rm{m}}/\sqrt {3{\rm{x}} + 7}  – \sqrt {{\rm{x}} + 1}  = 2.\)

\({\rm{n}}/\sqrt {11 – {\rm{x}}}  – \sqrt {{\rm{x}} – 1}  = 2\).

o/ \(\sqrt {{{\rm{x}}^2} + 9}  – \sqrt {{{\rm{x}}^2} + 7}  = 2\).

p/ \(\sqrt {\rm{x}}  + \sqrt {{\rm{x}} – 5}  = \sqrt 5 \)

q/ \(\sqrt {3{\rm{x}} – 5}  + \sqrt {2{\rm{x}} + 3}  = \sqrt {{\rm{x}} + 2} .\)

r/ \(\sqrt {{\rm{x}} – 2}  + \sqrt {{\rm{x}} – 1}  = \sqrt {2{\rm{x}} – 3} \)

s/ \(\sqrt {{\rm{x}} + 3}  – \sqrt {7 – {\rm{x}}}  = \sqrt {2{\rm{x}} – 8} .\quad \)

 t/ \(\sqrt {2 – {\rm{x}}}  = \sqrt {7 – {\rm{x}}}  – \sqrt { – 3 – 2{\rm{x}}} \).

\({\rm{u}}/\sqrt {5{\rm{x}} – 1}  = \sqrt {3{\rm{x}} – 2}  – \sqrt {2{\rm{x}} – 1} .\quad \)

 v/ \(\sqrt {5{\rm{x}} – 1}  – \sqrt {{\rm{x}} – 1}  = \sqrt {2{\rm{x}} – 4} \)

\(x/\sqrt {x + 2}  – \sqrt {2x – 3}  = \sqrt {3x – 5} .\quad \)

y \(\quad \sqrt {x + 4}  – \sqrt {1 – x}  = \sqrt {1 – 2x} \)

Bài 5. Giải các phương trình sau

a/ \(1 + \sqrt {{\rm{x}} – 1}  = \sqrt {6 – {\rm{x}}} \).

b/ \(\sqrt {5{\rm{x}} – 1}  – \sqrt {3{\rm{x}} – 2}  – \sqrt {{\rm{x}} – 1}  = 0.\)

c/ \(\sqrt {\rm{x}}  + \sqrt {{\rm{x}} + 1}  = \sqrt {{\rm{x}} + 2} \).

d/ \(\sqrt {3{\rm{x}} + 1}  = 8 – \sqrt {{\rm{x}} + 1} \).

e/ \(\sqrt {3x – 3}  – \sqrt {5 – x}  = \sqrt {2x – 4} \).

f/ \(\sqrt {{\rm{x}} + 9}  = 5 – \sqrt {2{\rm{x}} + 4} \)

Dạng 2. Phương trình căn sử dụng đặt ẩn phụ

(1)Loại 1 \(af(x) + b\sqrt {(x)}  + c = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{t = \sqrt {f(x)} ,t \ge 0}\\{a{t^2} + bt + c = 0}\end{array}} \right.\).

(2) Loại 2 \(\sqrt {f(x)}  + \sqrt {g(x)}  + \sqrt {f(x) \cdot g(x)}  = h(x)\).

Đặt \(t = \sqrt {f(x)}  + \sqrt {g(x)} \).

(3) Loại 3. Đặt ẩn phụ đưa về hệ phương trình : \(\sqrt {{\rm{f}}({\rm{x}})}  + \sqrt {{\rm{g}}({\rm{x}})}  = {\rm{h}}({\rm{x}})\).

– Đặt \(u = {\rm{f}}({\rm{x}}),\quad {\rm{v}} = {\rm{g}}({\rm{x}})\) với \(u,{\rm{v}} \ge 0\).

– Đưa phương trình trên về hệ phương trình với hai ẩn là u và v.

Ta có thể giải dạng tổng quát dạng \(:\sqrt[n]{{{\rm{f}}({\rm{x}})}} + \sqrt[m]{{{\rm{g}}({\rm{x}})}} = {\rm{a}},\quad ({\rm{a}} = {\rm{const}})\).

Bài tập áp dụng

Bài 6. Giải các phương trình sau

a/ \({x^2} – 6x + 9 = 4\sqrt {{x^2} – 6x + 6} .\quad \)

b/ \(\sqrt {(x – 3)(8 – x)}  + 26 =  – {x^2} + 11x\)

c) \((x + 4)(x + 1) – 3\sqrt {{x^2} + 5x + 2}  = 6.\)

d)\((x + 5)(2 – x) = 3\sqrt {{x^2} + 3x} \)

e/ \({{\rm{x}}^2} + \sqrt {{{\rm{x}}^2} + 11}  = 31\)

f/ \({{\rm{x}}^2} – 2{\rm{x}} + 8 – 4\sqrt {(4 – {\rm{x}})({\rm{x}} + 2)}  = 0\)

\({\rm{g}}/4{{\rm{x}}^2} – 12{\rm{x}} – 5\sqrt {4{{\rm{x}}^2} – 12{\rm{x}} + 11}  = 0.\)

\({\rm{h}}/{{\rm{x}}^2} + 4{\rm{x}} – 3|2 + {\rm{x}}| + 4 = 0\)

i/ \(4{{\rm{x}}^2} + \frac{1}{{{{\rm{x}}^2}}} + \left| {2{\rm{x}} – \frac{1}{{\rm{x}}}} \right| – 6 = 0.\)

j/ \({x^2} – x + \sqrt {{x^2} – x + 9}  = 3.\)

\({\rm{k}}/{{\rm{x}}^2} + 2\sqrt {{{\rm{x}}^2} – 3{\rm{x}} + 11}  = 3{\rm{x}} + 4\)

l/ \({{\rm{x}}^2} – 3{\rm{x}} – 10 + 3\sqrt {{\rm{x}}({\rm{x}} + 3)}  = 0\)

\({\rm{m}}/{{\rm{x}}^2} + 3{\rm{x}} – 18 + 4\sqrt {{{\rm{x}}^2} + 3{\rm{x}} – 6}  = 0.\quad \)

\({\rm{n}}/2{\rm{x}} – {{\rm{x}}^2} + \sqrt {6{{\rm{x}}^2} – 12{\rm{x}} + 7}  = 0\)

o/ \(({\rm{x}} + 4)({\rm{x}} + 1) – 3\sqrt {{{\rm{x}}^2} + 5{\rm{x}} + 2}  = 0.\quad \)

\({\rm{p}}/\quad {({\rm{x}} – 3)^2} + 3{\rm{x}} – 22 = \sqrt {{{\rm{x}}^2} – 3{\rm{x}} + 7} \)

q/ \(\quad {{\rm{x}}^2} + 1 – 7\sqrt {{{\rm{x}}^2} + 1}  + 10 = 0.\)

\({\rm{r}}/\sqrt {2{{\rm{x}}^2} – 8{\rm{x}} + 12}  = {{\rm{x}}^2} – 4{\rm{x}} – 6\)

Bài 7. Giải các phương trình sau

a/ \(\sqrt {{\rm{x}} + 3}  + \sqrt {6 – {\rm{x}}}  = 3 + \sqrt {({\rm{x}} + 3)(6 – {\rm{x}})} .\quad \)

b/ \(\sqrt {2{\rm{x}} + 3}  + \sqrt {{\rm{x}} + 1}  = 3{\rm{x}} + 2\sqrt {(2{\rm{x}} + 3)({\rm{x}} + 1)}  – 16.\)

c/ \(\sqrt {{\rm{x}} – 1}  + \sqrt {3 – {\rm{x}}}  – \sqrt {({\rm{x}} – 1)(3 – {\rm{x}})}  = 1.\)

\({\rm{d}}/\sqrt {7 – {\rm{x}}}  + \sqrt {2 + {\rm{x}}}  – \sqrt {(7 – {\rm{x}})(2 + {\rm{x}})}  = 3\)

e/ \(\sqrt {{\rm{x}} + 1}  + \sqrt {4 – {\rm{x}}}  + \sqrt {({\rm{x}} + 1)(4 – {\rm{x}})}  = 5.\quad \)

f \(/\sqrt {3{\rm{x}} – 2}  + \sqrt {{\rm{x}} – 1}  = 4{\rm{x}} – 9 + 2\sqrt {3{{\rm{x}}^2} – 5{\rm{x}} + 2} \)

\({\rm{g}}/1 + \frac{2}{3}\sqrt {{\rm{x}} – {{\rm{x}}^2}}  = \sqrt {\rm{x}}  + \sqrt {1 – {\rm{x}}} .\quad \)

\({\rm{h}}/\sqrt {\rm{x}}  + \sqrt {9 – {\rm{x}}}  = \sqrt { – {{\rm{x}}^2} + 9{\rm{x}} + 9} \)

\[{\rm{i}}/{\rm{x}} + \sqrt {17 – {{\rm{x}}^2}}  + {\rm{x}}\sqrt {17 – {{\rm{x}}^2}}  = 9.\]

\[{\rm{j}}/\sqrt {{\rm{x}} – 1}  + \sqrt {{\rm{x}} + 3}  + 2\sqrt {({\rm{x}} – 1)({\rm{x}} + 3)}  = 4 – 2{\rm{x}}\]

\({\rm{k}}/\sqrt {{\rm{x}} + 4}  + \sqrt {{\rm{x}} – 4}  = 2{\rm{x}} – 12 + 2\sqrt {{{\rm{x}}^2} – 16} .\)

\(1/\quad \sqrt {2{\rm{x}} + 3}  + \sqrt {{\rm{x}} + 1}  = 3{\rm{x}} + 2\sqrt {2{{\rm{x}}^2} + 5{\rm{x}} + 3}  – 16\)

\({\rm{m}}/\sqrt {3{\rm{x}} – 2}  + \sqrt {{\rm{x}} – 1}  = 4{\rm{x}} – 9 + 2\sqrt {3{{\rm{x}}^2} – 5{\rm{x}} + 2} .\quad \)

\({\rm{n}}/\sqrt {3{{\rm{x}}^2} + 6{\rm{x}} + 16}  + \sqrt {{{\rm{x}}^2} + 2{\rm{x}}}  = 2\sqrt {{{\rm{x}}^2} + 2{\rm{x}} + 4} \)

Bài 8. Giải các phương trình sau

a/ \(2\sqrt {\frac{{3x – 1}}{x}}  = \frac{x}{{3x – 1}} + 1\).

b/ \(\sqrt[3]{{{\rm{x}} + 7}} – \sqrt {\rm{x}}  = 1\)

c/ \(\sqrt[3]{{2 – {\rm{x}}}} = 1 – \sqrt {{\rm{x}} – 1} \)

\({\rm{d}}/\sqrt {{\rm{x}} + 3}  – \sqrt[3]{{\rm{x}}} = 1\)

e/ \({x^3} + 2 = 3\sqrt[3]{{3x – 2}}\)

f/ \(\sqrt[5]{{\frac{{16{\rm{x}}}}{{{\rm{x}} – 1}}}} + \sqrt[5]{{\frac{{{\rm{x}} – 1}}{{16{\rm{x}}}}}} = \frac{5}{2}\)

g/ \(\sqrt[3]{{\frac{{2x}}{{x + 1}}}} + \sqrt[3]{{\frac{1}{2} + \frac{1}{{2x}}}} = 2\)

\({\rm{h}}/\frac{{3 + {\rm{x}}}}{{3{\rm{x}}}} = \sqrt {\frac{1}{9} + \frac{1}{{\rm{x}}}\sqrt {\frac{4}{9} + \frac{2}{{{{\rm{x}}^2}}}} } \).

i/ \({\rm{x}} + \sqrt {4 – {{\rm{x}}^2}}  = 2 + 3{\rm{x}}\sqrt {4 – {{\rm{x}}^2}} \)

\({\rm{j}}/2\sqrt[4]{{{{(1 + x)}^2}}} + 3\sqrt[4]{{1 – {x^2}}} + \sqrt[4]{{{{(1 – x)}^2}}} = 0\)

k/ \(\sqrt[4]{{5 – x}} + \sqrt[4]{{4 – x}} = \sqrt 2 \)

1/ \(2\sqrt[3]{{3{\rm{x}} – 2}} + 3\sqrt {6 – 5{\rm{x}}}  – 8 = 0\)

\({\rm{m}}/\sqrt[3]{{{\rm{x}} + 3}} = 1 + \sqrt {\rm{x}} \)

\({\rm{n}}/\sqrt[3]{{{\rm{x}} + 34}} – \sqrt[3]{{{\rm{x}} – 3}} = 1\)

Dạng 3. Đưa về phương trình tích số( nhóm, liên hiệp,…)

– Đoán nhận một nghiệm của phương trình để định hướng đưa về phương trình tích số hoặc nhân liên hiệp.

– Cần chú ý đến các cách biến đổi về tích và nhân liên hiệp

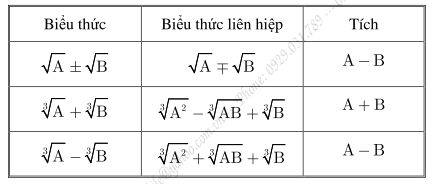
– \({\rm{f}}({\rm{x}}) = {\rm{a}}{{\rm{x}}^2} + {\rm{bx}} + {\rm{c}} = {\rm{a}}\left( {{\rm{x}} – {{\rm{x}}_1}} \right)\left( {{\rm{x}} – {{\rm{x}}_2}} \right)\) với \({{\rm{x}}_1}\) và \({{\rm{x}}_2}\) là hai nghiệm của \({\rm{f}}({\rm{x}}) = 0\).

\(*\quad {\rm{u}} + {\rm{v}} = 1 + {\rm{uv}} \Leftrightarrow ({\rm{u}} – 1)({\rm{v}} – 1) = 0\)

\(*\quad {\rm{au}} + {\rm{bv}} = {\rm{ab}} + {\rm{vu}} \Leftrightarrow ({\rm{u}} – {\rm{b}})({\rm{v}} – {\rm{a}}) = 0\)

–  Cần lưu ý đến các hằng đẳng thức( kết hợp đồng nhất thức)

Bài tập áp dụng

Giải các phương trình sau

a/ \((x – 3)\sqrt {{x^2} + 4}  = {x^2} – 9.\quad \)

b/ \((x – 3)\sqrt {{x^2} – 5x + 4}  = 2x – 6\)

c/ \((x + 3)\sqrt {10 – {x^2}}  = {x^2} – x – 12.\quad \)

d \(/(x + 1)\sqrt {16x + 17}  = 8{x^2} – 15x – 23.\)

e/ \(\sqrt {2{{\rm{x}}^2} + 8{\rm{x}} + 6}  + \sqrt {{{\rm{x}}^2} – 1}  = 2{\rm{x}} + 2.\quad \)

f/ \(\quad \sqrt {{{\rm{x}}^2} + 10{\rm{x}} + 21}  = 3\sqrt {{\rm{x}} + 3}  + 2\sqrt {{\rm{x}} + 7}  – 6\)

g/ \({\rm{x}} + 2\sqrt {7 – {\rm{x}}}  = 2\sqrt {{\rm{x}} – 1}  + \sqrt { – {{\rm{x}}^2} + 8{\rm{x}} – 7}  + 1.\).

\({\rm{h}}/\sqrt {\rm{x}}  + \sqrt {{\rm{x}} + 1}  – \sqrt {{{\rm{x}}^2} + {\rm{x}}}  = {\rm{x}}\)

i/ \(\sqrt {{x^2} – x – 2}  – 2\sqrt {x – 2}  + 2 = \sqrt {x + 1} .\quad \)

 j/ \(\quad \sqrt {{x^2} – 3x + 2}  + \sqrt {x + 3}  = \sqrt {x – 2}  + \sqrt {{x^2} + 2x – 3} \).

\({\rm{k}}/\sqrt {{\rm{x}}({\rm{x}} – 1)}  + \sqrt {{\rm{x}}({\rm{x}} + 2)}  = 2\sqrt {{{\rm{x}}^2}} .\quad \)

l/ \(\sqrt {{{\rm{x}}^2} – 8{\rm{x}} + 15}  + \sqrt {{{\rm{x}}^2} + 2{\rm{x}} – 15}  = \sqrt {{{\rm{x}}^2} – 9{\rm{x}} + 18} \)

\({\rm{m}}/2{{\rm{x}}^2} + 5{\rm{x}} – 1 = 7\sqrt {{{\rm{x}}^3} – 1} \)

\({\rm{n}}/\sqrt {2{\rm{x}} – 1}  + {{\rm{x}}^2} – 3{\rm{x}} + 1 = 0.\)

o/ \(\frac{{{{\rm{x}}^2}}}{{\sqrt {3{\rm{x}} – 2} }} – \sqrt {3{\rm{x}} – 2}  = 1 – {\rm{x}}\)

\({\rm{p}}/\sqrt[3]{{{\rm{x}} + 1}} + \sqrt[3]{{{\rm{x}} + 2}} = 1 + \sqrt[3]{{{{\rm{x}}^2} + 3{\rm{x}} + 2}}\)

q/ \(\sqrt[3]{{{\rm{x}} + 1}} + \sqrt[3]{{{{\rm{x}}^2}}} = \sqrt[3]{{\rm{x}}} + \sqrt[3]{{{{\rm{x}}^2} + {\rm{x}}}}.\)

\({\rm{r}}/\sqrt {{\rm{x}} + 3}  + 2{\rm{x}}\sqrt {{\rm{x}} + 1}  = 2{\rm{x}} + \sqrt {{{\rm{x}}^2} + 4{\rm{x}} + 3} \)

s/ \(\sqrt {{\rm{x}} + 3}  + \frac{{4{\rm{x}}}}{{\sqrt {{\rm{x}} + 3} }} = 4\sqrt {\rm{x}} \)

\({\rm{t}}/\sqrt {{\rm{x}} + 1}  + 2({\rm{x}} + 1) = {\rm{x}} – 1 + \sqrt {1 – {\rm{x}}}  + 3\sqrt {1 – {{\rm{x}}^2}} \)

Bài 10. Giải phương trình

a/ \(\sqrt {4{\rm{x}} + 1}  – \sqrt {3{\rm{x}} – 2}  = \frac{{{\rm{x}} + 3}}{5}.\quad \)

b/ \(\frac{4}{{{\rm{x}} + \sqrt {{{\rm{x}}^2} + {\rm{x}}} }} – \frac{1}{{{\rm{x}} – \sqrt {{{\rm{x}}^2} + {\rm{x}}} }} = \frac{3}{{\rm{x}}}\)

c/ \(\frac{1}{{1 – \sqrt {1 – {\rm{x}}} }} – \frac{1}{{1 + \sqrt {1 – {\rm{x}}} }} = \frac{{\sqrt 3 }}{{\rm{x}}}.\).

\({\rm{d}}/\sqrt {\rm{x}}  + \sqrt {{\rm{x}} + 1}  = \frac{1}{{\sqrt {\rm{x}} }}\)

e/ \(\sqrt {{{\rm{x}}^2} + 1}  – {\rm{x}} = \frac{5}{{2\sqrt {{{\rm{x}}^2} + 1} }}.\quad \)

f/ \(\frac{4}{{{\rm{x}} + \sqrt {{{\rm{x}}^2} + {\rm{x}}} }} – \frac{1}{{{\rm{x}} – \sqrt {{{\rm{x}}^2} + {\rm{x}}} }} = \frac{3}{{\rm{x}}}\)

\({\rm{g}}/4{({\rm{x}} + 1)^2} = (2{\rm{x}} + 10){(1 – \sqrt {3 + 2{\rm{x}}} )^2}.\quad \)

h/ \(2{{\rm{x}}^2} = ({\rm{x}} + 9){(2 – \sqrt {9 + 2{\rm{x}}} )^2}\)

i/ \({\rm{x}} + \sqrt {{{\rm{x}}^2} + 16}  = \frac{{40}}{{\sqrt {{{\rm{x}}^2} + 16} }}\).

j\(/\frac{{3{\rm{x}}}}{{\sqrt {3{\rm{x}} + 10} }} = \sqrt {3{\rm{x}} + 1}  – 1\)

\({\rm{k}}/\sqrt {2{\rm{x}} + 4}  – 2\sqrt {2 – {\rm{x}}}  = \frac{{3{\rm{x}} – 2}}{{\sqrt 3 }}\). \(\quad \)

l/ \((\sqrt {1 + {\rm{x}}}  – 1)(\sqrt {1 – {\rm{x}}}  + 1) = 2{\rm{x}}\).

\({\rm{m}}/\sqrt {3{\rm{x}} + 1}  – \sqrt {6 – {\rm{x}}}  + 3{{\rm{x}}^2} – 14{\rm{x}} – 8 = 0.\)

\({\rm{n}}/\sqrt[3]{{{{\rm{x}}^2} – 1}} + {\rm{x}} = \sqrt {{{\rm{x}}^3} – 2} \)

o/ \(\sqrt {{{\rm{x}}^2} + 12}  + 5 = 3{\rm{x}} + \sqrt {{{\rm{x}}^2} + 5} .\)

\({\rm{p}}/\sqrt {2{\rm{x}} + 4}  – 2\sqrt {2 – {\rm{x}}}  = \frac{{6{\rm{x}} – 4}}{{\sqrt {{{\rm{x}}^2} + 4} }}\)

Dạng 4. Sử dụng hằng đẳng thức đưa về phương trình cơ bản

(1) Loại 1 \( \cdot \sqrt[3]{{\rm{A}}} + \sqrt[3]{{\rm{B}}} = \sqrt[3]{{\rm{C}}}\quad (*)\)

Ta có

\(\begin{array}{l}(*) \Leftrightarrow {(\sqrt[3]{{\rm{A}}} + \sqrt[3]{{\rm{B}}})^3} = {(\sqrt[3]{{\rm{C}}})^3}\\ \Leftrightarrow {\rm{A}} + {\rm{B}} + 3\sqrt[3]{{{\rm{AB}}}}(\sqrt[3]{{\rm{A}}} + \sqrt[3]{{\rm{B}}}) = {\rm{C}}(**)\end{array}\)

Thay \(\sqrt[3]{{\rm{A}}} + \sqrt[3]{{\rm{B}}} = \sqrt[3]{{\rm{C}}}\) vào \((**)\), ta được: \((**) \Leftrightarrow {\rm{A}} + {\rm{B}} + 3\sqrt[3]{{{\rm{ABC}}}} = {\rm{C}}\).

(2) Loại 2. \(\sqrt {{\rm{f}}({\rm{x}})}  + \sqrt {{\rm{g}}({\rm{x}})}  = \sqrt {{\rm{h}}({\rm{x}})}  + \sqrt {{\rm{k}}({\rm{x}})} \)

 với \(\left[ {\begin{array}{*{20}{l}}{{\rm{f}}({\rm{x}}) + {\rm{h}}({\rm{x}}) = {\rm{g}}({\rm{x}}) + {\rm{k}}({\rm{x}})}\\{{\rm{f}}({\rm{x}}) \cdot {\rm{h}}({\rm{x}}) = {\rm{g}}({\rm{x}}) \cdot {\rm{k}}({\rm{x}})}\end{array}} \right.\)

– Biến đổi về dạng: \(\sqrt {{\rm{f}}({\rm{x}})}  – \sqrt {{\rm{h}}({\rm{x}})}  = \sqrt {{\rm{k}}({\rm{x}})}  – \sqrt {{\rm{g}}({\rm{x}})} \).

– Bình phương, giải phương trình hệ quả.

(3) Lọai 3. Căn trong căn

Sử dụng hẳng đẳng thức \({{\rm{a}}^2} + {{\rm{b}}^2} \pm 2{\rm{ab}} = {({\rm{a}} \pm {\rm{b}})^2}\) nhưng lưu ý

$\left|\text{A}\right|=\left\{\begin{array}{l}\text{A}\\ \text{A}\end{array}\right.$$\begin{array}{l}\text{ khi A}\ge 0\\ \text{ khi A}<0\end{array}$. Đưa về phương trình căn cơ bản.

Bài tập áp dụng

Bài 11. Giải phương trình

a/ \(2\sqrt {{\rm{x}} + 2 + 2\sqrt {{\rm{x}} + 1} }  – \sqrt {{\rm{x}} + 1}  = 4\).

b/ \(\sqrt {{\rm{x}} + 2\sqrt {{\rm{x}} – 1} }  – \sqrt {{\rm{x}} – 2\sqrt {{\rm{x}} – 1} }  =  – 2\).

c/ \(\sqrt {{\rm{x}} – 1 – 2\sqrt {{\rm{x}} – 2} }  – \sqrt {{\rm{x}} + 2 + 4\sqrt {{\rm{x}} – 2} }  + 3 = 0\)

d \(/\sqrt {2{\rm{x}} – 4 + 2\sqrt {2{\rm{x}} – 5} }  + \sqrt {2{\rm{x}} + 4 + 6\sqrt {2{\rm{x}} – 5} }  = 14\).

e/ \(\sqrt {{\rm{x}} + 5 – 4\sqrt {{\rm{x}} + 1} }  + \sqrt {{\rm{x}} + 2 – 2\sqrt {{\rm{x}} + 1} }  = 1\).

f/ \(\sqrt {2{\rm{x}} – 2\sqrt {2{\rm{x}} – 1} }  – 2\sqrt {2{\rm{x}} + 3 – 4\sqrt {2{\rm{x}} – 1} }  + 3\sqrt {2{\rm{x}} + 8 – 6\sqrt {2{\rm{x}} – 1} }  = 4\)

g/ \(\sqrt {{\rm{x}} + 3 – 4\sqrt {{\rm{x}} – 1} }  + \sqrt {{\rm{x}} + 8 – 6\sqrt {{\rm{x}} – 1} }  = 1\).

\({\rm{h}}/\sqrt {{\rm{x}} + 8 – 6\sqrt {{\rm{x}} – 1} }  – \sqrt {{\rm{x}} + 3 + 4\sqrt {{\rm{x}} – 1} }  + 5 = 0\).

i/ \(\sqrt {2{\rm{x}} – 4 – 2\sqrt {2{\rm{x}} – 5} }  – \sqrt {2{\rm{x}} + 4 + 6\sqrt {2{\rm{x}} – 5} }  + 4 = 0\).

\({\rm{j}}/\sqrt {2{\rm{x}} – 2 + 2\sqrt {2{\rm{x}} – 3} }  = 4 + \sqrt {2{\rm{x}} – 6 – 6\sqrt {2{\rm{x}} – 3} } \).

\({\rm{k}}/\sqrt {{\rm{x}} + 2\sqrt {{\rm{x}} – 1} }  + \sqrt {{\rm{x}} – 2\sqrt {{\rm{x}} – 1} }  = \frac{{{\rm{x}} + 3}}{2}\).

l/ \(\sqrt {{\rm{x}} + \sqrt {2{\rm{x}} – 1} }  + \sqrt {{\rm{x}} – \sqrt {2{\rm{x}} – 1} }  = \sqrt 2 \).

\({\rm{m}}/\sqrt {{\rm{x}} – 3 – 2\sqrt {{\rm{x}} – 4} }  + \sqrt {{\rm{x}} – 2\sqrt {{\rm{x}} – 1} }  = 1\).

\({\rm{n}}/\sqrt {{\rm{x}} + \sqrt {14{\rm{x}} – 49} }  + \sqrt {{\rm{x}} – \sqrt {14{\rm{x}} – 49} }  = \sqrt {14} \).

o/ \(21{\rm{x}} – 63 + 7\sqrt {10 – 4|3{\rm{x}} – 9|}  = 0.\)

Bài 12. Giải phương trình

a/ \(\sqrt[3]{{{\rm{x}} + 1}} + \sqrt[3]{{{\rm{x}} + 2}} + \sqrt[3]{{{\rm{x}} + 3}} = 0\)

b/ \(\sqrt[3]{{2{\rm{x}} – 1}} + \sqrt[3]{{{\rm{x}} – 1}} = \sqrt[3]{{3{\rm{x}} – 2}}\)

c/ \(\sqrt[3]{{{\rm{x}} + 5}} + \sqrt[3]{{{\rm{x}} + 6}} = \sqrt[3]{{2{\rm{x}} + 11}}\)

\({\rm{d}}/\sqrt[3]{{{\rm{x}} + 1}} + \sqrt[3]{{3{\rm{x}} + 1}} = \sqrt[3]{{{\rm{x}} – 1}}\)

e/ \(\sqrt[3]{{{\rm{x}} + 2}} + \sqrt[3]{{{\rm{x}} + 1}} = \sqrt[3]{{2{{\rm{x}}^2}}} + \sqrt[3]{{2{{\rm{x}}^2} + 1}}\quad \)

f/ \(\sqrt[3]{{2{\rm{x}} – 1}} + \sqrt[3]{{{\rm{x}} – 1}} + \sqrt[3]{{3{\rm{x}} – 2}} = 0\)

\({\rm{g}}/\sqrt[3]{{2{\rm{x}} + 1}} + \sqrt[3]{{2{\rm{x}} + 2}} + \sqrt[3]{{2{\rm{x}} + 3}} = 0.\)

\({\rm{h}}/\sqrt[3]{{\rm{x}}} + \sqrt[3]{{2{\rm{x}} – 3}} = \sqrt[3]{{12({\rm{x}} – 1)}}\)

Bài 13. Giải phương trình

a/ \(\sqrt {{\rm{x}} + 3}  + \sqrt {3{\rm{x}} + 1}  = 2\sqrt {\rm{x}}  + \sqrt {2{\rm{x}} + 2} \).

b/ \(\sqrt {\frac{{{{\rm{x}}^3} + 1}}{{{\rm{x}} + 3}}}  + \sqrt {{\rm{x}} + 1}  = \sqrt {{{\rm{x}}^2} – {\rm{x}} + 1}  + \sqrt {{\rm{x}} + 3} \).

c/ \(\sqrt {{{\rm{x}}^2} – 3{\rm{x}} + 2}  + \sqrt {{\rm{x}} + 3}  = \sqrt {6{\rm{x}} – 2}  + \sqrt {{{\rm{x}}^2} + 2{\rm{x}} – 3} \).

d \(/\sqrt {2{{\rm{x}}^2} – 1}  + \sqrt {{{\rm{x}}^2} – 3{\rm{x}} – 2}  = \sqrt {2{{\rm{x}}^2} + 2{\rm{x}} + 3}  + \sqrt {{{\rm{x}}^2} – {\rm{x}} + 2} \).

e/ \(\sqrt {3{{\rm{x}}^2} – 5{\rm{x}} + 1}  – \sqrt {{{\rm{x}}^2} – 2}  = \sqrt {3\left( {{{\rm{x}}^2} – {\rm{x}} – 1} \right)}  – \sqrt {{{\rm{x}}^2} – 3{\rm{x}} + 4} \).

f/ \(\sqrt {{{\rm{x}}^2} + 2}  + \sqrt {{{\rm{x}}^2} + 7}  = \sqrt {{{\rm{x}}^2} + {\rm{x}} + 3}  + \sqrt {{{\rm{x}}^2} + {\rm{x}} + 8} \).

g/ \(\sqrt {3{{\rm{x}}^2} – 7{\rm{x}} + 3}  – \sqrt {{{\rm{x}}^2} – 2}  = \sqrt {3{{\rm{x}}^2} – 5{\rm{x}} – 1}  – \sqrt {{{\rm{x}}^2} – 3{\rm{x}} + 4} \).

Bài 14. Giải phương trình

a/ \(4\sqrt[3]{{{{(x + 2)}^2}}} – 7\sqrt[3]{{\left( {4 – {x^2}} \right)}} + 3 \cdot \sqrt[3]{{{{(2 – x)}^2}}} = 0\).

b/ \(2\left( {{x^2} + 2} \right) = 5\sqrt {{x^3} + 1} \)

c/ \({{\rm{x}}^2} + 3\sqrt {{{\rm{x}}^2} – 1}  = \sqrt {{{\rm{x}}^4} – {{\rm{x}}^2} + 1} \)

Bài 15. Giải phương trình (đặt ẩn phụ không hoàn toàn)

a/ \({x^2} + 2(x – 1)\sqrt {{x^2} + x + 1}  – x + 2 = 0\)

b/ \(({\rm{x}} + 1)\sqrt {{{\rm{x}}^2} – 2{\rm{x}} + 3}  = {{\rm{x}}^2} + 1\)

\(c/(4x – 1)\sqrt {{x^2} + 1}  = 2{x^2} + 2x + 1\)

\({\rm{d}}/\sqrt {{{\rm{x}}^2} + 12}  + 5 = 3{\rm{x}} + \sqrt {{{\rm{x}}^2} + 5} \).

Ngoài cách giai thông thưởng ở trên, ta còn môt số phương pháp giải khác

– Phuơng pháp đánh giá dùng các bất đẳng thức cơ bản: BD Cauchy, BD Bunhiacopski, BDT  hinh hoc, ……

– Phương pháp lượng giác hóa

– Phương pháp khảo sát hàm số

– ……….

Xem thêm