Sách bài tập Tin học 10 Bài 17, 18 (Cánh diều): Thực hành lập trình giải bài toán trên máy tính

Giải SBT Tin học lớp 10 Bài 17, 18: Thực hành lập trình giải bài toán trên máy tính

Câu F86 trang 50 SBT Tin 10: Chia kẹo

Xét bài toán: Đội Trúc Xanh gồm 3 bạn An, Thuỳ và Minh đứng đầu trong cuộc thi về ca dao, tục ngữ Việt Nam. Cách trao giải của Ban tổ chức cũng khá độc đáo. Trên bàn bày một dãy n túi kẹo, trên túi kẹo thứ i có ghi số nguyên a_i, là số lượng kẹo trong túi (a_i ≥ 0). Đội thắng cuộc được phép chọn các túi kẹo có số lượng chia hết cho 3. Đội Trúc Xanh quyết định sẽ chọn hết tất cả các túi có kẹo và được phép lấy. Sau đó từ mỗi túi, mỗi người ăn một chiếc kẹo. Phần kẹo còn lại được tập trung và chia đều để mỗi bạn mang về cho em ở nhà. Hãy xác định, mỗi bạn đã ăn bao nhiêu cái kẹo và mang về nhà bao nhiêu cái.

Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu.

Dữ liệu: Nhập vào từ thiết bị vào chuẩn:

– Dòng đầu tiên chứa số nguyên n (1$\le n\le$10⁵).

– Dòng thứ hai chứa n số nguyên a₁, a₂,…, a_n (0$\le a_i\le$10⁴, i = 1, 2, …, n)

Kết quả: Đưa ra thiết bị ra chuẩn hai số nguyên là số lượng kẹo tương ứng với số kẹo mỗi bạn đã ăn và số kẹo mỗi bạn mang về, các số đưa ra trên cùng một dòng.

Ví dụ:

Input	Output
9 25      16      11      12      14      0        8        30      21	3 18

 

Trả lời:

Tóm tắt bài toán (Mô hình toán học)

Cho:

– Số nguyên n, (1 $\le n\le$10⁵) và n số nguyên a₁, a₂,.., a_n (0 ≤ a_i ≤10⁴, i = 1, 2, .., n).

Yêu cầu:

– Xác định k là số lượng a_i lớn hơn 0 và chia hết cho 3.

– Tính tổng (a_i – 3)/3 với các a_i tìm được.

Thuật toán và cách tổ chức dữ liệu

– Bước 1. Nhập dữ liệu vào (dùng kiểu danh sách cho dãy n số nguyên).

– Bước 2. Chuẩn bị tích luỹ số lượng và tổng: k = 0, s = 0.

– Bước 3. Duyệt với mọi i: Nếu a_i > 0 và a_i chia hết cho 3 thì tăng k và tích luỹ a_i vào s.

– Bước 4. Đưa ra k và (s – 3k)/3.

Tham khảo chương trình sau:

Câu F87 trang 50 SBT Tin 10: Điểm dừng xe

Xét bài toán: Các điểm dừng đón, trả khách của xe buýt cách đều nhau một đoạn k mét. Điểm dừng đầu tiên ở đầu phố. Như vậy tính từ đầu phố, xe buýt dừng ở các điểm 0, k, 2k, 3k,… (mét). Nhà của Tâm ở ngay đầu phố. Để kết hợp rèn luyện thể lực, Tâm thường đi bộ tới trường. Hôm nay, khi đi bộ được n mét, Tâm chợt nhớ cần phải tới sớm theo lời hẹn với một người bạn nên quyết định sẽ bắt xe buýt ở trạm tiếp theo gần nhất. Hãy xác định Tâm còn phải đi thêm bao nhiêu mét nữa.

Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu.

Dữ liệu: Nhập vào từ thiết bị vào chuẩn, dòng đầu tiên chứa số nguyên k, dòng thứ hai chứa số nguyên n (1 ≤ k, n ≤ 2×10⁹).

Kết quả: Đưa ra thiết bị ra chuẩn một số nguyên là độ dài đoạn đường cần đi tiếp (tính theo mét).

Ví dụ:

Input	Output
800 2 100	300

 

Trả lời:

Tóm tắt bài toán (Mô hình toán học)

Cho:

– Các điểm (được đánh dấu) cách đều nhau k mét.

– Điểm đầu có toạ độ là 0.

– Điểm x có toạ độ là n.

Yêu cầu: Xác định khoảng cách gần nhất từ điểm x tới một điểm được đánh dấu.

Thuật toán và cách tổ chức dữ liệu:

– Bước 1. Nhập số nguyên k và n.

– Bước 2. Tính d là khoảng cách từ x tới điểm bên trái của x.

– Bước 3. Tìm min của khoảng cách từ x tới điểm bên trái x và bên phải của x.

– Bước 4. Đưa ra kết quả.

Tham khảo chương trình sau:

Câu F88 trang 51 SBT Tin 10: Số bị thiếu

Tâm nhờ một người bạn tạo dãy số nguyên dương a₁, a₂,…, a_n với $1\le a_i\le n$, i = 1, 2, …, n và các số khác nhau từng đôi một để làm dữ liệu đầu vào kiểm thử một chương trình mới viết. Khi nhận được kết quả, Tâm phát hiện ra bạn mình chỉ gửi có n – 1 số, các số nhận được thoả mãn những yêu cầu đã nêu. Tâm cần xác định số bị thiếu để có dữ liệu cần thiết.

Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu.

Dữ liệu: Nhập vào từ thiết bị vào chuẩn, dòng đầu tiên chứa số nguyên n, ($3\le n\le {10}^6$), dòng thứ 2 chứa n – 1 số nguyên dương a₁, a₂,…, a_n thoả mãn các ràng buộc đã nêu, các số cách nhau một dấu cách.

Kết quả: Đưa ra thiết bị ra chuẩn số nguyên còn thiếu.

Ví dụ:

Input	Output
5    2        5        1        4	3

 

Trả lời:

Tóm tắt bài toán (Mô hình toán học)

Cho: n và n – 1 số nguyên a₁, a₂,…, a_n-1 . Trong đó a_i ≠ a_j, với i ≠ j, $1\le a_i\le n$ với mọi i.

Yêu cầu: Tìm số bị thiếu không vượt quá n.

Thuật toán và cách tổ chức dữ liệu

– Nếu có đầy đủ n số thì tổng các số sẽ là $\frac{n\times (n+1)}{2}$

– Vậy số còn thiếu là: $\frac{n\times (n+1)}{2}-\sum _{i=0}^{n-2}{a}_i$

– Không cần phải dùng dãy để lưu các số nhập vào.

– Các bước của thuật toán:

+ Bước 1. Nhập n.

+ Bước 2. Nhập và tính tổng các a_i

+ Bước 3. Đưa ra kết quả.

Tham khảo chương trình sau:

Câu F89 trang 51 SBT Tin 10: Trung vị

Xét bài toán: Cho dãy số nguyên A = (a₁, a₂,…, a_n). Phần tử x của dãy được gọi là phần tử trung vị nếu nó lớn hơn hoặc bằng $\left[\frac{n}{2}\right]$ phần tử của dãy và nhỏ hơn hoặc bằng các phần tử còn lại trong dãy. Ví dụ, với A = (8, 1, 6, 3, 9, 2, 3, l, 7) trung vị là phần tử có giá trị là 5. Tìm và đưa ra giá trị của phần tử trung vị của dãy A bất kì.

Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu. Khi viết xong chương trình thì đề xuất ít nhất thêm hai bộ dữ liệu để kiểm thử chương trình.

Dữ liệu: Nhập vào từ thiết bị vào chuẩn một dòng chứa các phần tử của dãy, các số cách nhau một dấu cách.

Kết quả: Đưa ra thiết bị ra chuẩn giá trị của phần tử trung vị của dãy.

Ví dụ:

Input	Output
8        1        6        5        9        2        3        1        7	5

 

Trả lời:

Tóm tắt bài toán (Mô hình toán học)

Cho: Dãy A gồm n số nguyên.

Yêu cầu: Đưa ra phân tử trung vị (phần tử nằm ở giữa dãy đã sắp xếp).

Thuật toán và chọn kiểu dữ liệu cho các biến

– Bước 1. Nhập số nguyên n, nhập danh sách A chứa n số nguyên.

– Bước 2. Sắp xếp danh sách A.

– Bước 3. Đưa ra phần tử A [len (A) //2].

Tham khảo chương trình sau:

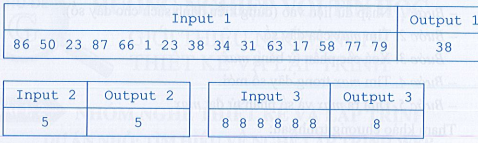
Ví dụ một số bộ dữ liệu để kiểm thử chương trình:

Câu F90 trang 52 SBT Tin 10: Lớp II

Các nhà thiên văn phân loại đối tượng trên vùng trời đang nghiên cứu theo cường độ bức xạ Gamma của chúng. Đối tượng thứ i có cường độ bức xạ g_i, (g_i là số thực và lớn hơn 0, i= 1,2,…, n). Các đối tượng được phân thành từng lớp: lớp I gồm các đối tượng có cùng cường độ bức xạ Gamma lớn nhất; lớp II gồm các đối tượng có cùng cường độ bức xạ Gamma lớn thứ hai,…

Xác định số lượng đối tượng lớp II và cường độ bức xạ Gamma của đối tượng thuộc lớp này.

Em hãy lập trình giải bài toán trên. Trước khi lập trình cần tóm tắt bài toán, xác định thuật toán và cách tổ chức dữ liệu. Khi viết xong chương trình thì đề xuất thêm ít nhất hai bộ dữ liệu để kiểm thử chương trình.

Dữ liệu: Nhập vào từ thiết bị vào chuẩn gồm một dòng chứa các số thực dương g₁, g₂,…, g_n.

Kết quả: Đưa ra thiết bị ra chuẩn trên một dòng, mỗi số cách nhau một dấu cách, số thứ nhất là số nguyên xác định số lượng đối tượng thuộc lớp II, số thứ hai là số thực xác định cường độ bức xạ của lớp II.

Ví dụ:

Input	Output
1.5  2.63  1.04  4.12  2.63  4.12  2.63	3  2.63

 

Trả lời:

Tóm tắt bài toán (Mô hình toán học)

Cho n số thực dương dương g₁, g₂,…, g_n.

Yêu cầu: tìm giá trị lớn thứ hai của dãy số và số phần tử đạt giá trị này.

Thuật toán 1 và cách tổ chức dữ liệu

– Bước 1. Nhập dữ liệu, lưu theo chỉ số bắt đầu từ 0 (dùng kiểu danh sách để chứa dãy số).

– Bước 2. Sắp xếp dãy số theo thứ tự giảm dần.

– Bước 3. Đếm số phần tử đạt max → k.

– Bước 4. Đếm số phần tử có giá trị đạt g_k

– Bước 5. Đưa ra các giá trị tìm được.

Tham khảo chương trình sau:

Nhận xét: Chương trình trên đơn giản nhưng mất nhiều thời gian thực hiện vì phải sắp xếp

Thuật toán 2 và cách tổ chức dữ liệu

– Bước 1. Nhập dữ liệu vào (dùng kiểu danh sách cho dãy số).

– Bước 2. Tìm max của dãy số.

– Bước 3. Xoá các phần tử bằng max.

– Bước 4. Tìm max trong dãy số mới.

– Bước 5. Đưa ra max và số phần tử đạt max.

Tham khảo chương trình sau:

Ví dụ một số bộ dữ liệu để kiểm thử chương trình:

Xem thêm các bài giải SBT Tin học lớp 10 Cánh diều hay, chi tiết khác:

SBT Tin học 10 Bài 16: Kiểm thử và gỡ lỗi chương trình

SBT Tin học 10 Bài 17, 18: Thực hành lập trình giải bài toán trên máy tính

Lý thuyết Tin học 10 Bài 18: Lập trình giải quyết bài toán trên máy tính

SBT Tin học 10 Bài 1, 2: Nhóm nghề thiết kế và lập trình – Dự án nhỏ: Tìm hiểu về nghề lập trình web, lập trình trò chơi và lập trình cho thiết bị di động

SBT Tin học 10 Bài 1, 2: Hệ nhị phân và ứng dụng – Thực hành về các phép toán bit và hệ nhị phân