Lý thuyết Tính đơn diệu và cực trị của hàm số (Chân trời sáng tạo 2024) | Lý thuyết Toán 12

Lý thuyết Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số

A. Lý thuyết Tính đơn điệu và cực trị của hàm số

1. Tính đơn điệu của hàm số

Định lý 1

Cho hàm số y = f(x) có đạo hàm trên K Nếu f’(x) > 0 với mọi x thuộc K thì hàm số f(x) đồng biến trên K. Nếu f’(x) < 0 với mọi x thuộc K thì hàm số f(x) nghịch biến trên K.

Chú ý:

a) Nếu hàm số y = f(x) có đạo hàm trên K, f’(x)  0 với mọi x thuộc K và f’(x) = 0 chỉ tại một số hữa hạn điểm của K thì hàm số f(x) đồng biến trên K.

b) Nếu hàm số y = f(x) có đạo hàm trên K, f’(x)  0 với mọi x thuộc K và f’(x) = 0 chỉ tại một số hữa hạn điểm của K thì hàm số f(x) nghịch biến trên K.

c) Nếu f’(x) = 0 với mọi x thuộc K thì hàm số không đổi trên K.

2. Cực trị của hàm số

Khái niệm cực trị của hàm số

Cho hàm số y = f(x) liên tục trên tập $K\subset R$, trong đó K là một khoảng, đoạn hoặc nửa khoảng và $x_0\in K,x_1\in K$ $x_0$ được gọi là một điểm cực đại của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm $x_0$ sao cho (a;b) $\subset$ K và $f(x)<f(x_0)$ với mọi $x\in (a;b)$ và $x\ne x_0$. Khi đó, $f(x_0)$ được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là $f_{CĐ}$ $x_1$ được gọi là một điểm cực tiểu của hàm số đã cho nếu tồn tại một khoảng (a;b) chứa điểm $x_0$ sao cho (c;d) $\subset$ K và $f(x)>f(x_1)$ với mọi $x\in (c;d)$ và $x\ne x_1$. Khi đó, $f(x_1)$ được gọi là giá trị cực đại của hàm số đã cho, kí hiệu là $f_{CT}$ Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại và giá trị cực tiểu được gọi chung là giá trị cực trị (hay cực trị)

Định lý 

Giả sử hàm số y = f(x) liên tục trên khoảng (a;b) chứa điểm $x_0$ và có đạo hàm trên các khoảng $\left(a;x_0\right)$ và $\left(x_0;b\right)$. Khi đó: a) Nếu f’(x) < 0 với mọi $x\in \left(a;x_0\right)$ và f’(x) > 0 với mọi $x\in \left(x_0;b\right)$ thì hàm số f(x) đạt cực tiểu tại điểm $x_0$ b) Nếu f’(x) > 0 với mọi $x\in \left(a;x_0\right)$ và f’(x) < 0 với mọi $x\in \left(x_0;b\right)$ thì hàm số f(x) đạt cực tiểu tại điểm $x_0$

Sơ đồ tư duy Tính đơn diệu và cực trị của hàm số

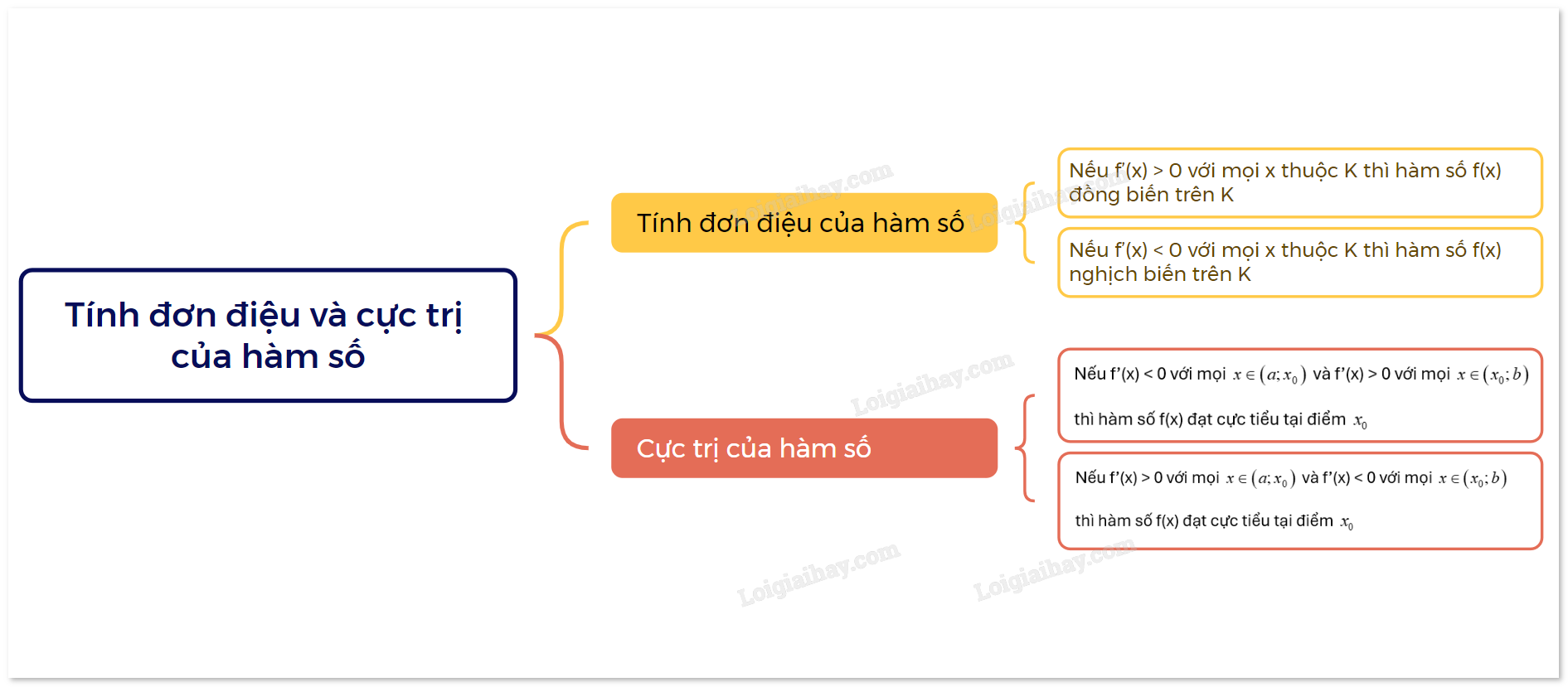
B. Bài tập Tính đơn điệu và cực trị của hàm số

Bài 1. Cho hàm số y = f(x) xác định, liên tục trên ℝ và có đồ thị như hình vẽ. Mệnh đề nào sau đây đúng?

A. Hàm số đồng biến trên (−∞; 1).

B. Hàm số đồng biến trên khoảng (−∞; −1).

C. Hàm số đồng biến trên khoảng (0; +∞).

D. Hàm số đồng biến trên khoảng (−3; +∞).

Hướng dẫn giải

Đáp án đúng là: B

Dựa vào đồ thị hàm số, ta thấy hàm số đồng biến trên khoảng (−∞; −1).

Bài 2. Cho hàm số y = f(x) có bảng biến thiên như sau

Mệnh đề nào dưới đây sai?

A. Hàm số có giá trị cực đại bằng 3.

B. Hàm số có hai điểm cực tiểu.

C. Hàm số có giá trị cực đại bằng 0.

D. Hàm số có 3 điểm cực trị.

Hướng dẫn giải

Đáp án đúng là: C

Dựa vào bảng biến thiên, ta có:

Hàm số đạt cực đại tại x = 0 và y_CĐ = 3.

Hàm số đạt cực tiểu tại x = −1; x = 1 và y_CT = 0.

Do đó đáp án C sai.

Bài 3. Xét tính đơn điệu của các hàm số sau:

a) y = x⁴ + 4x²;

b) $y=\frac{-x^2+2x-1}{x+2}$

Hướng dẫn giải

a) Tập xác định: D = ℝ.

Có y’ = 4x³ + 8x; y’ = 0 $\iff$ x = 0.

Bảng biến thiên

Vậy hàm số đồng biến trên khoảng (0; +∞) và nghịch biến trên khoảng (−∞; 0).

b) Tập xác định: D = ℝ\{−2}.

Có $y^{‘}=\frac{\left(-2x+2\right)\left(x+2\right)-\left(-x^2+2x-1\right)}{{\left(x+2\right)}^2}=\frac{-x^2-4x+5}{{\left(x+2\right)}^2}$

Có y’ = 0 $\iff$ −x² – 4x + 5 = 0 $\iff$ x = 1 hoặc x = −5.

Bảng biến thiên

Vậy hàm số nghịch biến trên các khoảng (−∞; −5) và (1; +∞).

Hàm số đồng biến trên các khoảng (−5; −2) và (−2; 1).

Bài 4.Tìm cực trị của các hàm số sau

a) y = x³ – 6x² + 9x;

b) $y=\frac{2x-2}{x+1}$

Hướng dẫn giải

a) Tập xác định: D = ℝ.

Có y’ = 3x² – 12x + 9; y’ = 0 $\iff$ x = 1 hoặc x = 3.

Bảng biến thiên

Vậy hàm số đạt cực đại tại x = 1 và y_CĐ = 4.

Hàm số đạt cực tiểu tại x = 3 và y_CT = 0.

b) Tập xác định: D = ℝ\{−1}.

Có $y^{‘}=\frac{2\left(x+1\right)-\left(2x-2\right)}{{\left(x+1\right)}^2}=\frac{4}{{\left(x+1\right)}^2}>0,\forall x\ne -1$

Do đó hàm số luôn đồng biến trên các khoảng (−∞; −1) và (−1; +∞).

Hàm số không có cực trị.

Bài 5. Thể tích nước của một bể bơi sau t phút bơm tính theo công thức $V\left(t\right)=\frac{1}{100}\left(30t^3-\frac{t^4}{4}\right)$, (0 ≤ t ≤ 90). Tốc độ bơm nước tại thời điểm t được tính bởi f(t) = V'(t). Trong khoảng thời gian nào tốc độ bơm tăng? Trong khoảng thời gian nào tốc độ bơm giảm?

Hướng dẫn giải

Với 0 ≤ t ≤ 90,

Có $f\left(t\right)=V^{‘}\left(t\right)=\frac{9}{10}{t}^2-\frac{1}{100}{t}^3$

Có $f^{‘}\left(t\right)=V^{”}\left(t\right)=\frac{9}{5}t-\frac{3}{100}{t}^2$ ; f'(t) = 0 $\iff$ t = 0 hoặc t = 60.

Bảng biến thiên

Dựa vào bảng biến thiên ta thấy:

Tốc độ bơm tăng từ phút 0 đến phút 60, tốc độ bơm giảm từ phút 60 đến phút 90.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 12 Chân trời sáng tạo hay, chi tiết khác:

Lý thuyết Bài 1: Tính đơn diệu và cực trị của hàm số

Lý thuyết Bài 2: Giá trị lớn nhất, giá trị nhỏ nhất của hàm số

Lý thuyết Bài 3: Đường tiệm cận của đồ thị hàm số

Lý thuyết Bài 4: Khảo sát và vẽ đồ thị một số hàm số cơ bản

Lý thuyết Bài 1: Vectơ và các phép toán trong không gian

Lý thuyết Bài 2: Toạ độ của vectơ trong không gian