Câu hỏi:
Cho hình lăng trụ đứng \({\mkern 1mu} ABCD.A’B’C’D’\) có đáy là hình thoi có cạnh \(4a\), \(A’A = 8a\), \(\widehat {BAD} = {120^{0.}}\). Gọi \(M,N,K\) lần lượt là trung điểm cạnh \(AB’,B’C,BD’\). Thể tích khối da diện lồi có các đỉnh là các điểm \(A,B,C,M,N,K\) là:
A. \(12\sqrt 3 {\mkern 1mu} {a^3}\)
Đáp án chính xác
B. \(\frac{{28\sqrt 3 }}{3}{\mkern 1mu} {a^3}\)
C. \(16\sqrt 3 {\mkern 1mu} {a^3}\)
D. \(\frac{{40\sqrt 3 }}{3}{\mkern 1mu} {a^3}\)
Trả lời:
Đáp án A

\({\rm{MN // AC}};{\rm{ MN}} = \frac{1}{2}AC,{\rm{ MNCA}}\) là hình thang.
\({V_{MNK{\rm{A}}BC}} = {V_{K.MNCA}} + {V_{B.MNCA}}\)
DK cắt \(\left( {B’AC} \right)\) tại \(B’\), \(\frac{{B’K}}{{B’D}} = \frac{1}{2} \Rightarrow \frac{{d\left( {K;(MNC{\rm{D}})} \right)}}{{d\left( {D;(MNCA)} \right)}} = \frac{1}{2} \Rightarrow {V_{K.MNCA}} = \frac{1}{2}{V_{D.MNCA}}\)
Mà: \({V_{B.MNCA}} = {V_{D.MNCA}}\) nên ta có: \({V_{MNK{\rm{A}}BC}} = \frac{1}{2}{V_{B.MNCA}} + {V_{B.MNCA}} = \frac{3}{2}{V_{B.MNCA}}\)
Mặt khác: \({S_{MNCA}} = \frac{3}{4}{S_{B’AC}} \Rightarrow {V_{B.MNCA}} = \frac{3}{4}{V_{B.B’AC}} = \frac{3}{4}{V_{B’.ABC}} = \frac{3}{4}.\frac{1}{6}{V_{ABCD.A’B’C’D’}} = 8\sqrt 3 {a^3}\)
\({V_{MNKABC}} = \frac{3}{2}{V_{B.MNCA}} = \frac{3}{2}8\sqrt 3 {\mkern 1mu} {a^3} = 12\sqrt 3 {\mkern 1mu} {a^3}\).
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm \(A\left( {1; – 1;2} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {2;2; – 1} \right).\) Phương trình của (P) là
Câu hỏi:
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) đi qua điểm \(A\left( {1; – 1;2} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {2;2; – 1} \right).\) Phương trình của (P) là
A. \(2x + 2y – z – 6 = 0.\)
B. \(2x + 2y – z + 2 = 0.\)
Đáp án chính xác
C. \(2x + 2y – z + 6 = 0.\)
D. \(2x + 2y – z – 2 = 0.\)
Trả lời:
Đáp án B
Phương trình \(\left( P \right)\) là: \(2{\rm{x}} + 2y – z + 2 = 0\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số cho dưới đây?
Câu hỏi:
Đường cong trong hình vẽ bên là đồ thị của hàm số nào trong các hàm số cho dưới đây?
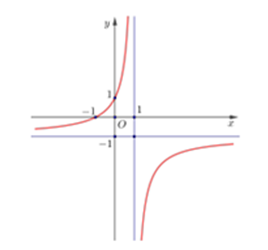
A. \(y = \frac{{ – x – 1}}{{x – 1}}\)
Đáp án chính xác
B. \(y = \frac{{x + 1}}{{x – 1}}\)
C. \(y = \frac{{ – x + 1}}{{x + 1}}\)
D. \(y = \frac{{x – 1}}{{x + 1}}\)
Trả lời:
Đáp án A
Đồ thị hàm số có tiệm cận ngang và tiệm cận đứng lần lượt là \(y = 1;x = – 1\).
Ngoài ra hàm số đồng biến trên tập xác định. Chọn A hoặc C.
Tiếp tục tính đạo hàm để loại trừ.====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Trong mặt phằng cho 10 điểm phân biệt. Số vectơ khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối lấy trong các điểm đã cho là
Câu hỏi:
Trong mặt phằng cho 10 điểm phân biệt. Số vectơ khác \(\overrightarrow 0 \), có điểm đầu và điểm cuối lấy trong các điểm đã cho là
A. \({2^{10}}\)
B. \(A_{10}^2\)
Đáp án chính xác
C. \(10!\)
D. \(C_{10}^2\)
Trả lời:
Đáp án B
Số vectơ (phân biệt điểm đầu, điểm cuối) là \(A_{10}^2\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {0;1} \right]\) và \(f\left( 1 \right) – f\left( 0 \right) = 2\). Tính \(I = \int\limits_0^1 {\left[ {f'\left( x \right) – {e^x}} \right]dx} \).
Câu hỏi:
Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên đoạn \(\left[ {0;1} \right]\) và \(f\left( 1 \right) – f\left( 0 \right) = 2\). Tính \(I = \int\limits_0^1 {\left[ {f’\left( x \right) – {e^x}} \right]dx} \).
A. \(1 – e\)
B. \(1 + e\)
C. \(3 – e\)
Đáp án chính xác
D. \(3 + e\)
Trả lời:
Đáp án C
\(I = \int\limits_0^1 {f’\left( x \right)d{\rm{x}}} – \int\limits_0^1 {{e^x}d{\rm{x}}} = \left. {f\left( x \right)} \right|_0^1 – \left. {{e^x}} \right|_0^1 = f\left( 1 \right) – f\left( 0 \right) – \left( {e – 1} \right) = 2 – e + 1 = 3 – e\).====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tập nghiệm của bất phương trình \({3^{2x – 1}} > 27\) là:
Câu hỏi:
Tập nghiệm của bất phương trình \({3^{2x – 1}} > 27\) là:
A. \(\left( {3; + \infty } \right).\)
B. \(\left( {\frac{1}{3}; + \infty } \right).\)
C. \(\left( {\frac{1}{2}; + \infty } \right).\)
D. \(\left( {2; + \infty } \right).\)
Đáp án chính xác
Trả lời:
Đáp án D
\({3^{2{\rm{x}} – 1}} > 27 \Leftrightarrow {3^{2{\rm{x}} – 1}} > {3^3} \Leftrightarrow 2{\rm{x}} – 1 > 3 \Leftrightarrow x > 2\)
Vậy tập nghiệm của bất phương trình là \(\left( {2; + \infty } \right)\).====== **** mời các bạn xem câu tiếp bên dưới **** =====