Câu hỏi:
Thực hiện phép tính (tính nhanh nếu có thể):a) 132 – 32 : 23b) 83.35 – 83.18 + 832c) 125 – 5.[18 + 54 : (9 – 2.3)2]
Trả lời:
Lời giải:a) 132 – 32 : 23= 132 – 32 : 8= 132 – 4= 128b) 83.35 – 83.18 + 832= 83.(35 – 18 + 83)= 83.100= 8300c) 125 – 5.[18 + 54 : (9 – 2.3)2]= 125 – 5.[18 + 54 : 32]= 125 – 5.[18 + 54 : 9]= 125 – 5.[18 + 6]= 125 – 5.24= 125 – 120= 5
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm số tự nhiên x biết:a) 95 – 5(x + 2) = 45b) 5x – 1 – 2.52= 3.52c) x + 11 là bội của x + 2
Câu hỏi:
Tìm số tự nhiên x biết:a) 95 – 5(x + 2) = 45b) 5x – 1 – 2.52= 3.52c) x + 11 là bội của x + 2
Trả lời:
Lời giải:a) 95 – 5(x + 2) = 455(x + 2) = 95 – 455(x + 2) = 50x + 2 = 50 : 5x + 2 = 10x = 10 – 2 x = 8Vậy x = 8.b) 5x – 1 – 2.52= 3.525x – 1 = 3.52 + 2.525x – 1 = 5.52 5x – 1 = 53x – 1 = 3x = 4Vậy x = 4.c) x + 11 là bội của x + 2⇒ (x + 11) ⁝ (x + 2)⇒ (x + 2 + 9) ⁝ (x + 2)⇒ 9 ⁝ (x + 2) (tính chất chia hết của một tổng)⇒ (x + 2) ∈ Ư(9) = {–1; –3; –9; 1; 3; 9}⇒ x ∈ {–3; –5; –11; –1; 1; 7}Mà \(x \in \mathbb{N}\)⇒ x ∈ {1; 7}Vậy x ∈ {1; 7}.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm các chữ số a và b biết số\(\overline {a12b} \) chia hết cho 2 và 9, đồng thời chia cho 5 dư 1.
Câu hỏi:
Tìm các chữ số a và b biết số\(\overline {a12b} \) chia hết cho 2 và 9, đồng thời chia cho 5 dư 1.
Trả lời:
Lời giải:
Điều kiện: 0 < a ≤ 9, 0 ≤ b ≤ 9; a, b \( \in \mathbb{N}\)
Ta có \(\overline {a12b} \) chia hết cho 2 và 9, chia 5 dư 1
⇒ b = 6
Ta có \(\overline {a126} \vdots 9\)
⇒ (a + 1 + 2 + 6) ⁝ 9 (tổng các chữ số chia hết cho 9)
⇒ (a + 9) ⁝ 9 (a là số tự nhiên khác 0 và nhỏ hơn hoặc bằng 9)
⇒ a = 9 (áp dụng tính chất chia hết của một tổng)
Vậy số phải tìm là 9126.
</>====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Lớp 6A có 28 học sinh nam và 21 học sinh nữ được chia đều vào các tổ, biết số tổ là một số nguyên tố. Hỏi lớp 6A có bao nhiêu tổ? Mỗi tổ có bao nhiêu bạn nam? Có bao nhiêu bạn nữ?
Câu hỏi:
Lớp 6A có 28 học sinh nam và 21 học sinh nữ được chia đều vào các tổ, biết số tổ là một số nguyên tố. Hỏi lớp 6A có bao nhiêu tổ? Mỗi tổ có bao nhiêu bạn nam? Có bao nhiêu bạn nữ?
Trả lời:
Lời giải:Gọi số tổ đã chia là xTa có 28 ⁝ x và 21 ⁝ x⇒ x ∈ ƯC(28, 21)28 = 4.7 và 21 = 3.7ƯCLN(28, 21) = 7x = ƯC(28, 21) = Ư(7) = {1; 7}Vậy lớp có thể có 7 tổ và mỗi tổ có 4 bạn nam và 3 bạn nữ.
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- a) Hình vẽ bên là hình ảnh của một chiếc rubic – 4 mặt, mỗi mặt đều được ghép bởi những tam giác đều nhỏ bằng nhau. Con hãy đếm số tam giác đều có trên một mặt của chiếc rubic này?b) Trên mảnh đất hình chữ nhật, có chiều dài 8m và chiều rộng 5m, người ta làm một bồn hoa hình thoi như hình vẽ. Tính diện tích phần còn lại của mảnh đất.
Câu hỏi:
a) Hình vẽ bên là hình ảnh của một chiếc rubic – 4 mặt, mỗi mặt đều được ghép bởi những tam giác đều nhỏ bằng nhau. Con hãy đếm số tam giác đều có trên một mặt của chiếc rubic này?
b) Trên mảnh đất hình chữ nhật, có chiều dài 8m và chiều rộng 5m, người ta làm một bồn hoa hình thoi như hình vẽ. Tính diện tích phần còn lại của mảnh đất.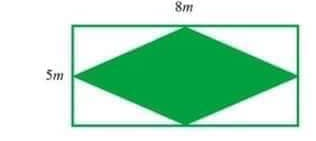
Trả lời:
Lời giải:a) Một mặt của chiếc rubic gồm:9 tam giác đều nhỏ3 tam giác đều vừa1 tam giác đều toVậy một mặt của chiếc rubic có 9 + 3 + 1 = 13 tam giác đều.b) Diện tích mảnh đất hình chữ nhật là:8.5 = 40 (m2)Diện tích bồn hoa hình thoi là:\(\frac{1}{2}.8.5 = 20\)(m2)Vậy diện tích còn lại của mảnh đất là:40 – 20 = 20 (m2)
====== **** mời các bạn xem câu tiếp bên dưới **** =====
- Tìm số tự nhiên nhỏ nhất khác 0 sao cho khi chia nó cho 2 thì được một số chính phương. Khi chia nó cho 3 thì được lập phương của một số tự nhiên.
Câu hỏi:
Tìm số tự nhiên nhỏ nhất khác 0 sao cho khi chia nó cho 2 thì được một số chính phương. Khi chia nó cho 3 thì được lập phương của một số tự nhiên.
Trả lời:
Lời giải:Gọi số phải tìm là n; a là số chính phương; b là số tự nhiên mà n là lập phương của nó.Ta thấy n chia hết cho 2 và 3 (vì số chính phương hay lập phương của một số tự nhiên đều là số tự nhiên) nên n nhỏ nhất, ta chọn n = 2x.3y(x và y khác 0)n : 2 = 2x.3y: 2 = 2x – 1.3y= a2⇒ x – 1 và y đều chia hết cho 2 hay đều là số chẵn. (1)n : 3 = 2x.3y: 3 = 2x .3y – 1= b3⇒ x và y – 1 đều chia hết cho 3. (2)Từ (1) và (2) để x đạt nhỏ nhất ⇒ x = 3Từ (1) và (2) để y đạt nhỏ nhất ⇒ y = 4Vậy n = 23.34= 648.Vậy số cần tìm là 648.
====== **** mời các bạn xem câu tiếp bên dưới **** =====