Bài 2 trang 33 sách bài tập Toán lớp 6 Tập 2: Tính giá trị biểu thức 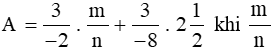nhận các giá trị:

By admin 06/06/2023 0

Câu hỏi:

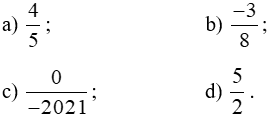
Bài 2 trang 33 sách bài tập Toán lớp 6 Tập 2: Tính giá trị biểu thức Tính giá trị biểu thức A = 3/-2. m/n nhận các giá trị:

Trả lời:

Lời giải:
a) Với 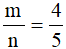Tính giá trị biểu thức A = 3/-2. m/n thì:

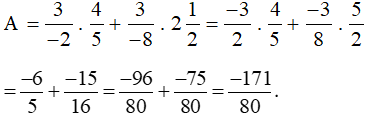
Vậy với 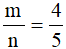 thì giá trị biểu thức A là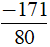
b) Với 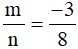 thì:

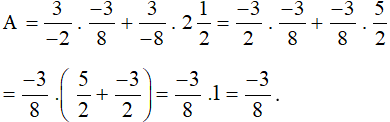
Vậy với 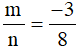 thì giá trị biểu thức A là
c) Với 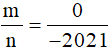 thì:
.
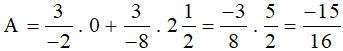Vậy với 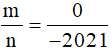 thì giá trị biểu thức A là .
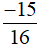d) Với 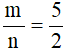 thì:

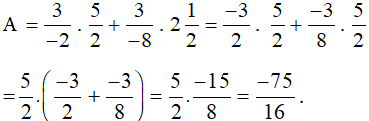
Vậy với  thì giá trị biểu thức A là Tính giá trị biểu thức A 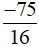= 3/-2. m/n .

====== **** mời các bạn xem câu tiếp bên dưới **** =====

Giải SGK Toán 7 (Cánh diều): Bài tập cuối chương 5

Giải bài tập Toán lớp 7 Bài tập cuối chương 5

Giải Toán 7 trang 34 Tập 2

Bài 1 trang 34 Toán 7 Tập 2: Biểu đồ cột ở Hình 33 biểu diễn kim ngạch xuất khẩu hàng hoá (ước đạt) của tỉnh Bình Dương vào các năm 2016, 2017, 2018, 2019, 2020.

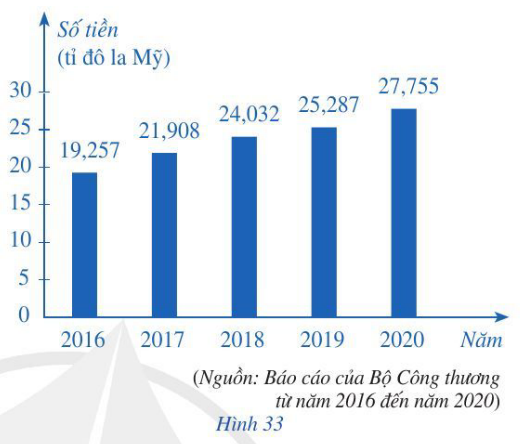
Giải Toán 7 (Cánh diều): Bài tập cuối chương 5 (ảnh 1)

a) Kim ngạch xuất khẩu hàng hoá năm 2020 của tỉnh Bình Dương tăng bao nhiêu phần trăm so với năm 2016?

b) Trong giai đoạn từ năm 2016 đến năm 2020, kim ngạch xuất khẩu hàng hoá của tỉnh Bình Dương trung bình là bao nhiêu tỉ đô la Mỹ?

c) Hoàn thành số liệu ở bảng sau:

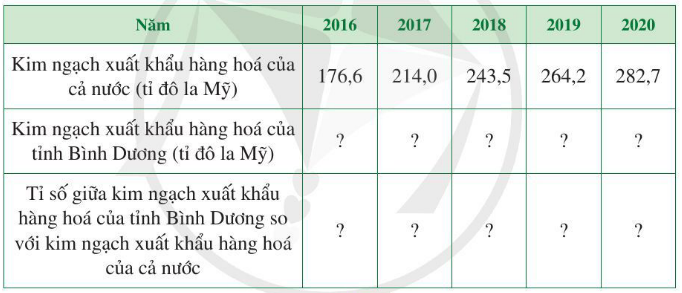
Giải Toán 7 (Cánh diều): Bài tập cuối chương 5 (ảnh 1)

Lời giải:

a) Quan sát biểu đồ Hình 33 ta thấy:

– Kim ngạch xuất khẩu hàng hoá năm 2016 của tỉnh Bình Dương là: 19,257 tỉ đô la Mỹ;

– Kim ngạch xuất khẩu hàng hoá năm 2020 của tỉnh Bình Dương là: 27,755 tỉ đô la Mỹ.

Tỉ số phần trăm của kim ngạch xuất khẩu hàng hoá năm 2020 so với năm 2016 của tỉnh Bình Dương là:

$\frac{27,755.100}{19,257} % \approx 144,13 %$

Vậy kim ngạch xuất khẩu hàng hoá năm 2020 của tỉnh Bình Dương tăng 44,13% so với năm 2016.

b) Quan sát biểu đồ Hình 33 ta thấy:

– Kim ngạch xuất khẩu hàng hoá năm 2017 của tỉnh Bình Dương là: 21,908 tỉ đô la Mỹ;

– Kim ngạch xuất khẩu hàng hoá năm 2018 của tỉnh Bình Dương là: 24,032 tỉ đô la Mỹ.

– Kim ngạch xuất khẩu hàng hoá năm 2019 của tỉnh Bình Dương là: 25,287 tỉ đô la Mỹ.

Trong giai đoạn từ năm 2016 đến năm 2020, kim ngạch xuất khẩu hàng hoá của tỉnh Bình Dương trung bình là:

$\frac{19,257 + 21,908 + 24,032 + 25,287 + 27,755}{5} = 23,6478$ (tỉ đô la Mỹ)

Vậy trong giai đoạn từ năm 2016 đến năm 2020, kim ngạch xuất khẩu hàng hoá của tỉnh Bình Dương trung bình là 23,6478 tỉ đô la Mỹ.

c) Tỉ số giữa kim ngạch xuất khẩu hàng hoá năm 2016 của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hoá của cả nước là: $\frac{19,257}{176,6} = \frac{19257}{176600} \approx 0,109.$

Tỉ số giữa kim ngạch xuất khẩu hàng hoá năm 2017 của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hoá của cả nước là: $\frac{21,908}{214,0} = \frac{5477}{53500} \approx 0,102.$

Tỉ số giữa kim ngạch xuất khẩu hàng hoá năm 2018 của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hoá của cả nước là: $\frac{24,032}{243,5} = \frac{6008}{60875} \approx 0,099.$

Tỉ số giữa kim ngạch xuất khẩu hàng hoá năm 2019 của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hoá của cả nước là: $\frac{25,287}{264,2} = \frac{25287}{264200} \approx 0,096.$

Tỉ số giữa kim ngạch xuất khẩu hàng hoá năm 2020 của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hoá của cả nước là: $\frac{27,755}{282,7} = \frac{5551}{56540} \approx 0,098.$

Ta có bảng sau:

Năm	2016	2017	2018	2019	2020
Kim ngạch xuất khẩu hàng hoá của cả nước (tỉ đô la Mỹ)	176,6	214,0	243,5	264,2	282,7
Kim ngạch xuất khẩu hàng hoá của tỉnh Bình Dương (tỉ đô la Mỹ)	19,257	21,908	24,032	25,287	27,755
Tỉ số giữa kim ngạch xuất khẩu hàng hoá của tỉnh Bình Dương so với kim ngạch xuất khẩu hàng hoá của cả nước	0,109	0,102	0,099	0,096	0,098

Bài 2 trang 34, 35 Toán 7 Tập 2: Biểu đồ đoạn thẳng ở Hình 34 biểu diễn dân số của thế giới vào các năm 1804, 1927, 1959, 1974, 1987, 1999, 2011. Giả sử dân số thế giới tại các năm m và n (m < n) lần lượt là a và b. Ta gọi tốc độ tăng dân số từ năm m đến năm n là tỉ số $\frac{b - a}{n - m} .$

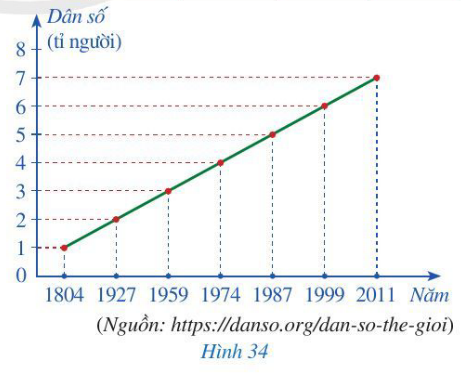
Giải Toán 7 (Cánh diều): Bài tập cuối chương 5 (ảnh 1)

a) Tính tốc độ tăng dân số thế giới:

– Từ năm 1804 đến năm 1927;

– Từ năm 1999 đến năm 2011.

b) Tốc độ tăng dân số thế giới từ năm 1999 đến năm 2011 gấp bao nhiêu lần tốc độ tăng dân số thế giới từ năm 1804 đến năm 1927?

c) Hoàn thành số liệu ở bảng sau:

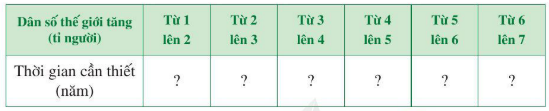
Giải Toán 7 (Cánh diều): Bài tập cuối chương 5 (ảnh 1)

d) Nêu nhận xét về tốc độ tăng dân số thế giới từ năm 1804 đến năm 2011.

Lời giải:

a) Tốc độ tăng dân số thế giới từ năm 1804 đến năm 1927 là: $\frac{2 - 1}{1927 - 1804} = \frac{1}{123} \approx 0,008.$

Tốc độ tăng dân số thế giới từ năm 1999 đến năm 2011 là: $\frac{7 - 6}{2011 - 1999} = \frac{1}{12} \approx 0,083.$

b) Tốc độ tăng dân số thế giới từ năm 1999 đến năm 2011 gấp số lần tốc độ tăng dân số thế giới từ năm 1804 đến năm 1927 là: $\frac{1}{12} : \frac{1}{123} = \frac{1}{12} .123 = 10,25$

Vậy tốc độ tăng dân số thế giới từ năm 1999 đến năm 2011 gấp 10,25 lần tốc độ tăng dân số thế giới từ năm 1804 đến năm 1927.

c) Thời gian cần thiết để dân số thế giới tăng từ 1 tỉ người lên 2 tỉ người (từ năm 1804 đến năm 1927) là:

1927 – 1804 = 123 (năm).

Thời gian cần thiết để dân số thế giới tăng từ 2 tỉ người lên 3 tỉ người (từ năm 1927 đến năm 1959) là:

1959 – 1927 = 32 (năm).

Thời gian cần thiết để dân số thế giới tăng từ 3 tỉ người lên 4 tỉ người (từ năm 1959 đến năm 1974 là:

1974 – 1959 = 15 (năm).

Thời gian cần thiết để dân số thế giới tăng từ 4 tỉ người lên 5 tỉ người (từ năm 1974 đến năm 1987 là:

1987 – 1974 = 13 (năm).

Thời gian cần thiết để dân số thế giới tăng từ 5 tỉ người lên 6 tỉ người (từ năm 1987 đến năm 1999 là:

1999 – 1987 = 12 (năm).

Thời gian cần thiết để dân số thế giới tăng từ 6 tỉ người lên 7 tỉ người (từ năm 1999 đến năm 2011 là:

2011 – 1999 = 12 (năm).

Ta có bảng sau:

Dân số thế giới tăng

(tỉ người)

Từ 1 lên 2

Từ 2 lên 3

Từ 3 lên 4

Từ 4 lên 5

Từ 5 lên 6

Từ 6 lên 7

Thời gian cần thiết

(năm)

123

d) Tốc độ tăng dân số thế giới từ năm 1804 đến năm 2011 là:

$\frac{7 - 1}{2011 - 1804} = \frac{6}{207} = \frac{2}{69} \approx 0,029.$

Nhận xét về tốc độ tăng dân số thế giới từ năm 1804 đến năm 2011: Tốc độ tăng dân số càng ngày càng tăng, thời gian cần thiết để dân số thế giới tăng thêm 1 tỉ người ngày càng ngắn.

Giải Toán 7 trang 35 Tập 2

Bài 3 trang 35 Toán 7 Tập 2: Theo kết quả tổng điều tra dân số và nhà ở năm 2019, dân số nước ta là 96 208 984 người và quy mô dân số theo sáu vùng kinh tế ‒ xã hội được biểu diễn bằng biểu đồ hình quạt tròn ở Hình 35.

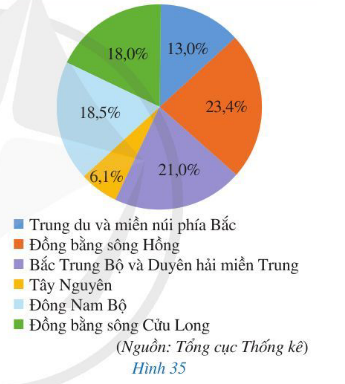
Giải Toán 7 (Cánh diều): Bài tập cuối chương 5 (ảnh 1)

a) Nêu quy mô dân số của mỗi vùng kinh tế ‒ xã hội của nước ta.

b) Vùng kinh tế – xã hội nào có quy mô dân số lớn nhất? Nhỏ nhất?

Lời giải:

a) Quan sát biểu đồ Hình 35, ta thấy

– Dân số vùng Trung du và miền núi phía Bắc chiếm 13,0% tổng dân số.

– Dân số vùng Đồng bằng sông Hồng chiếm 23,4% tổng dân số.

– Dân số vùng Bắc Trung Bộ và Duyên hải miền Trung chiếm 21,0% tổng dân số.

– Dân số vùng Tây Nguyên chiếm 6,1% tổng dân số.

– Dân số vùng Đông Nam Bộ chiếm 18,5% tổng dân số.

– Dân số vùng Đồng bằng sông Cửu Long chiếm 18,0% tổng dân số.

Do đó quy mô dân số của mỗi vùng kinh tế ‒ xã hội của nước ta năm 2019 là:

– Vùng Trung du và miền núi phía Bắc có:

$96 208 984.13,0 % = \frac{96 208 984.13,0}{100} \approx 12 507 168$ (người)

– Vùng Đồng bằng sông Hồng có:

$96 208 984.23,4 % = \frac{96 208 984.23,4}{100} \approx 22 512 902$ (người)

– Vùng Bắc Trung Bộ và Duyên hải miền Trung có:

$96 208 984.21,0 % = \frac{96 208 984.21,0}{100} \approx 20 203 887$ (người)

– Vùng Tây Nguyên có:

$96 208 984.6,1 % = \frac{96 208 984.6,1}{100} \approx 5 868 748$ (người)

– Vùng Đông Nam Bộ có:

$96 208 984.18,5 % = \frac{96 208 984.18,5}{100} \approx 17 798 662$ (người)

– Vùng Đồng bằng sông Cửu Long có:

$96 208 984.18,0 % = \frac{96 208 984.18,0}{100} \approx 17 317 617$ (người)

b) Vùng kinh tế – xã hội có quy mô dân số lớn nhất là vùng Đồng bằng sông Hồng (22 512 902 người).

Vùng kinh tế – xã hội có quy mô dân số nhỏ nhất là vùng Tây Nguyên (5 868 748 người).

Bài 4 trang 35 Toán 7 Tập 2: Biểu đồ ở Hình 36 biểu diễn tỉ lệ theo thể tích trong không khí của: khí oxygen; khí nitrogen; hơi nước, khí carbonic và các khí khác.

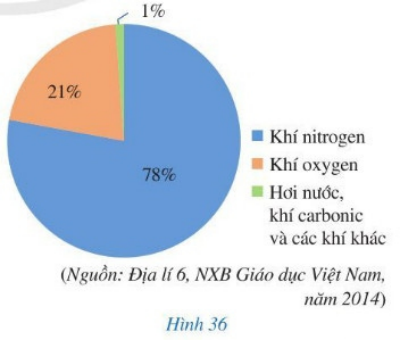
Giải Toán 7 (Cánh diều): Bài tập cuối chương 5 (ảnh 1)

Quan sát biểu đồ các thành phần của không khí ở Hình 36 và cho biết trong không khí, có bao nhiêu phần trăm là:

a) Khí nitrogen;

b) Khí oxygen;

c) Hơi nước, khí carbonic và các khí khác.

Lời giải:

Quan sát biểu đồ Hình 36 ta thấy:

a) Trong không khí có 78% là khí nitrogen.

b) Trong không khí có 21% là khí oxygen.

c) Trong không khí có 1% là hơi nước, khí carbonic và các khí khác.

Giải Toán 7 trang 36 Tập 2

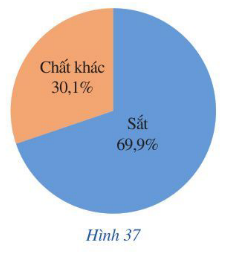
Bài 5 trang 36 Toán 7 Tập 2: Quặng sắt là các loại đá và khoáng vật mà từ đó sắt kim loại có thể được chiết ra. Quặng sắt thường giàu các sắt oxit và có màu sắc từ xám sẫm, vàng tươi, tía sẫm tới nâu đỏ. Quặng hematite là loại quặng sắt chính có trong các mỏ của nước Brasil. Tỉ lệ sắt trong quặng hematite được biểu diễn ở Hình 37. Trong 8 kg quặng hematite có bao nhiêu ki-lô-gam sắt?

Giải Toán 7 (Cánh diều): Bài tập cuối chương 5 (ảnh 1)

Lời giải:

Quan sát biểu đồ Hình 37 ta thấy sắt chiếm 69,9% trong quặng hematite.

Do đó trong 8 kg quặng hematite thì có số kg sắt là:

$8.69,9 % = \frac{8.69,9}{100} = 5,592$ (kg).

Bài 6 trang 36 Toán 7 Tập 2: Gieo ngẫu nhiên xúc xắc một lần. Tính xác suất của mỗi biến cố sau:

a) “Mặt xuất hiện của xúc xắc có số chấm là ước của 6”;

b) “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 2”.

Lời giải:

Khi gieo ngẫu nhiên xúc xắc một lần ta có tập hợp các kết quả có thể xảy ra đối với mặt xuất hiện của xúc xắc là: A = {mặt 1 chấm; mặt 2 chấm; mặt 3 chấm; mặt 4 chấm; mặt 5 chấm; mặt 6 chấm}.

a) Có bốn kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là ước của 6” là: mặt 1 chấm, mặt 2 chấm, mặt 3 chấm, mặt 6 chấm.

Vậy xác suất của biến cố trên là: $\frac{4}{6} = \frac{2}{3} .$

b) Có hai kết quả thuận lợi cho biến cố “Mặt xuất hiện của xúc xắc có số chấm là số chia 3 dư 2” là: mặt 2 chấm, mặt 5 chấm.

Vậy xác suất của biến cố trên là: $\frac{2}{6} = \frac{1}{3} .$

Bài 7 trang 36 Toán 7 Tập 2: Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 51, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:

a) “Số xuất hiện trên thẻ được rút ra là số khi chia cho 17 dư 2 và chia cho 3 dư l”;

b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5”.

Lời giải:

Khi rút ngẫu nhiên một thẻ trong hộp có 52 chiếc thẻ trên thì tập hợp những kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra là: A = {1; 2; 3; …; 51; 52}.

Số phần tử của tập hợp A là 52.

a) Có một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số khi chia cho 17 dư 2 và chia cho 3 dư l” là: 19.

Vậy xác suất của biến cố trên là: $\frac{1}{52} .$

b) Có tám kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5” là: 5, 15, 25, 35, 45, 50, 51, 52.

Vậy xác suất của biến cố trên là: $\frac{8}{52} = \frac{2}{13} .$

Bài 8 trang 36 Toán 7 Tập 2: Viết ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất của mỗi biến cố sau:

a) “Số tự nhiên được viết ra là số chia hết cho cả 2 và 5”;

b) “Số tự nhiên được viết ra là số có tổng các chữ số bằng 5”.

Lời giải:

Khi viết ngẫu nhiên một số tự nhiên có hai chữ số thì tập hợp gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra là: A = {10; 11; 12; …; 98; 99}.

Số phần tử của tập hợp A là: 99 – 10 + 1 = 90.

a) Có chín kết quả thuận lợi cho biến cố: “Số tự nhiên được viết ra là số chia hết cho cả 2 và 5” là: 10, 20, 30, …., 90.

Vậy xác suất của biến cố này là: $\frac{9}{90} = \frac{1}{10} .$

b) Có năm kết quả thuận lợi cho biến cố: “Số tự nhiên được viết ra là số có tổng các chữ số bằng 5” là: 14, 23, 32, 41, 50.

Vậy xác suất của biến cố này là: $\frac{5}{90} = \frac{1}{18} .$

Bài 9 trang 36 Toán 7 Tập 2: Một đội thanh niên tình nguyện gồm 27 thành viên đến từ các tỉnh: Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng, Phú Yên, Khánh Hoà, Ninh Thuận, Bình Thuận, Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh, Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang và Cà Mau; mỗi tỉnh chỉ có đúng một thành viên trong đội. Chọn ra ngẫu nhiên một thành viên của đội thanh niên trên. Tính xác suất của mỗi biến cố sau:

a) “Thành viên được chọn ra đến từ vùng Tây Nguyên”;

b) “Thành viên được chọn ra đến từ vùng Duyên hải miền Trung”;

c) “Thành viên được chọn ra đến từ vùng Đông Nam Bộ”;

d) “Thành viên được chọn ra đến từ vùng Đồng bằng sông Cửu Long”.

Lời giải:

Khi chọn ra ngẫu nhiên một thành viên của đội thanh niên trên ta có tập hợp gồm các kết quả có thể xảy ra đối với quê quán của thành viên là: A = {Kon Tum; Gia Lai; Đắk Lắk; Đắk Nông; Lâm Đồng; Phú Yên; Khánh Hoà; Ninh Thuận; Bình Thuận; Bà Rịa – Vũng Tàu; Bình Dương; Bình Phước; Đồng Nai; Tây Ninh; Long An; Tiền Giang; Vĩnh Long; Bến Tre; Đồng Tháp; Trà Vinh; An Giang; Cần Thơ; Hậu Giang; Bạc Liêu; Sóc Trăng; Kiên Giang; Cà Mau}.

Số phần tử của tập hợp A là 27.

a) Có năm kết quả thuận lợi cho biến cố: “Thành viên được chọn ra đến từ vùng Tây Nguyên” là: Kon Tum, Gia Lai, Đắk Lắk, Đắk Nông, Lâm Đồng.

Vậy xác suất của biến cố này là: $\frac{5}{27} .$

b) Có bốn kết quả thuận lợi cho biến cố: “Thành viên được chọn ra đến từ vùng Duyên hải miền Trung” là: Phú Yên, Khánh Hoà, Ninh Thuận, Bình Thuận.

Vậy xác suất của biến cố này là: $\frac{4}{27} .$

c) Có năm kết quả thuận lợi cho biến cố: “Thành viên được chọn ra đến từ vùng Đông Nam Bộ” là: Bà Rịa – Vũng Tàu, Bình Dương, Bình Phước, Đồng Nai, Tây Ninh.

Vậy xác suất của biến cố này là: $\frac{5}{27} .$

d) Có mười ba kết quả thuận lợi cho biến cố: “Thành viên được chọn ra đến từ vùng Đồng bằng sông Cửu Long” là: Long An, Tiền Giang, Vĩnh Long, Bến Tre, Đồng Tháp, Trà Vinh, An Giang, Cần Thơ, Hậu Giang, Bạc Liêu, Sóc Trăng, Kiên Giang, Cà Mau.

Vậy xác suất của biến cố này là: $\frac{13}{27} .$

Xem thêm các bài giải SGK Toán lớp 7 Cánh diều hay, chi tiết:

Giải SGK Toán 7 Bài 6: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản

Giải SGK Toán 7: Bài tập cuối chương 5

Giải SGK Toán 7 Bài 1: Biểu thức số. Biểu thức đại số

Giải SGK Toán 7 Bài 2: Đa thức một biến. Nghiệm của đa thức một biến

Giải SGK Toán 7 Bài 3: Phép cộng, phép trừ đa thức một biến

Giải SGK Toán 7 (Chân trời sáng tạo) Bài tập cuối chương 5

Giải bài tập Toán lớp 7 Bài tập cuối chương 5

Giải Toán 7 trang 109 Tập 1

Bài 1 trang 109 Toán lớp 7: Bảng thống kê dưới đây biểu diễn dữ liệu về chi tiêu của gia đình bạn Lan. Em hãy phân loại dữ liệu dựa trên các tiêu chí định tính và định lượng.

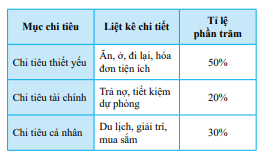
Phương pháp giải:

Các dữ liệu số là dữ liệu định lượng

Các dữ liệu không phải là số là dữ liệu định tính

Lời giải:

* Dữ liệu định tính:

+ Mục chi tiêu: Chi tiêu thiết yếu; chi tiêu tài chính; chi tiêu cá nhân.

+ Liệt kê chi tiết: Ăn, ở, đi lại, hóa đơn tiện ích; Trả nợ, tiết kiệm, dự phòng; Du lịch, giải trí, mua sắm.

* Dữ liệu định lượng: Tỉ lệ phần trăm: 50%, 20%, 30%

Bài 2 trang 109 Toán lớp 7: Thống kê điểm kiểm tra môn Toán của 10 học sinh giỏi Toán của lớp 7B, ta được dãy số liệu sau: 8;8;8;8,5;9;9;9;9,5;10;10.

Dữ liệu trên có đại diện cho kết quả kiểm tra Toán của lớp 7B hay không?

Phương pháp giải:

Dữ liệu mang tính đại diện đối với vấn đề khi thể hiện đủ dữ liệu của các đối tượng

Lời giải:

Dữ liệu trên không đại diện cho kết quả kiểm tra Toán của lớp 7B vì còn thiếu dữ liệu của các học sinh không phải học sinh giỏi Toán

Giải Toán 7 trang 110 Tập 1

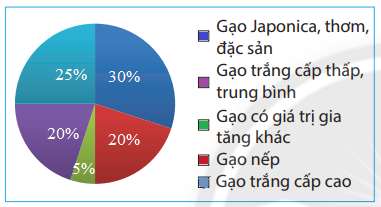
Bài 3 trang 110 Toán lớp 7: Tỉ lệ loại gạo xuất khẩu của Việt Nam năm 2020 được cho trong bảng dữ liệu sau đây. Em hãy biểu diễn thông tin từ bảng dữ liệu đã cho vào biểu đồ bên dưới.

Phương pháp giải:

+ Xác định và điền tỉ số phần trăm tương ứng với mỗi hình quạt

+ Tô màu biểu diễn đối tượng đó vào chú thích.

Lời giải:

Bài 4 trang 110 Toán lớp 7: Tập đoàn X có 6 công ty A,B,C,D,E,F. Trong năm 2020, tỉ lệ doanh thu của mỗi công ty so với tổng doanh thu của tập đoàn được biểu thị như biểu đồ sau:

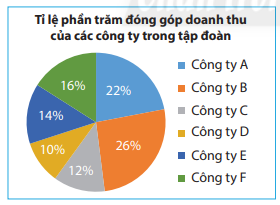
Dựa vào thông tin thu thập từ biểu đồ trên để trả lời các câu hỏi sau:

a) Nếu doanh thu của công ty D là 650 tỉ đồng thì doanh thu của công ty B là bao nhiêu tỉ đồng?

b) Tỉ lệ đóng góp của công ty F nhiều hơn công ty D là bao nhiêu phần trăm?

Phương pháp giải:

Xác định tỉ lệ phần trăm đóng góp doanh thu của mỗi công ty

a) Bước 1: Tính doanh thu của cả tập đoàn:

Tìm a biết m% của a là b, ta có: a = b : $\frac{m}{100}$

Bước 2: Tìm doanh thu của công ty B:

Tìm n% của a, ta có: a . $\frac{n}{100}$

b) Tính hiệu hai tỉ lệ phần trăm

Lời giải:

Công ty A,B,C,D,E,F lần lượt đóng góp vào tập đoàn: 22%; 26%; 12%; 10%; 14%; 16% tổng doanh thu của tập đoàn

a) Doanh thu của cả tập đoàn là:

$650 : \frac{10}{100} = 6500$ (tỉ đồng)

Doanh thu của công ty B là:

$6500. \frac{26}{100} = 1690$ (tỉ đồng)

b) Tỉ lệ đóng góp của công ty F nhiều hơn công ty D là:

16% – 10% = 6% (tổng doanh thu của tập đoàn)

Bài 5 trang 110 Toán lớp 7: Bảng dữ liệu sau cho biết số ổ bánh mì bán được ở căng tin trường Kim Đồng vào các ngày trong tuần vừa qua. Em hãy vẽ biểu đồ đoạn thẳng biểu diễn bảng dữ liệu này.

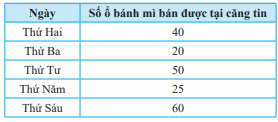
Phương pháp giải:

Cách vẽ biểu đồ đoạn thẳng:

Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau

– Trục ngang: Ghi các mốc thời gian

– Trục dọc: Chọn khoảng chia thích hợp với số liệu và ghi số ở các vạch chia

Bước 2:

– Tại mỗi mốc thời gian trên tục ngang, đánh dấu một điểm cách điểm mốc thời gian theo chiều thẳng đứng một khoảng bằng số liệu tại mốc thời gian đó, tương ứng với khoảng chia trên trục dọc

– Vẽ các đoạn thẳng nối từng cặp điểm tương ứng với cặp mốc thời gian liên tiếp, ta được một đường gấp khúc biểu diễn sự thay đổi số liệu theo thời gian.

Bước 3: Hoàn thiện biểu đồ:

– Ghi tên biểu đồ

– Ghi chú các giá trị số liệu tại các đầu đoạn thẳng

– Ghi đơn vị trên 2 trục

Lời giải:

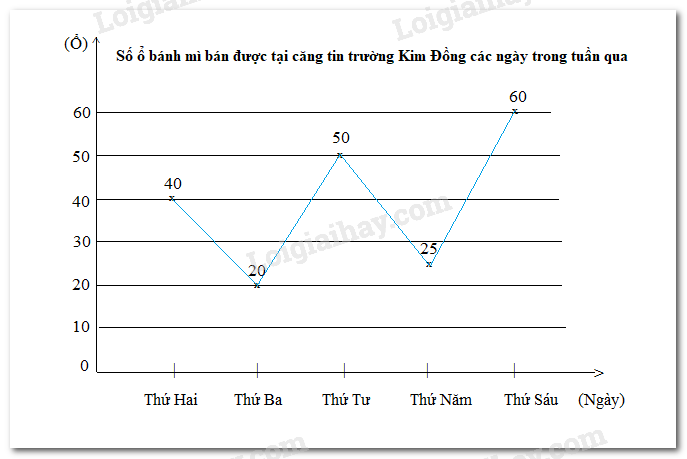
Bài 6 trang 110 Toán lớp 7: Hãy phân tích biểu đồ đoạn thẳng sau để trả lời các câu hỏi.

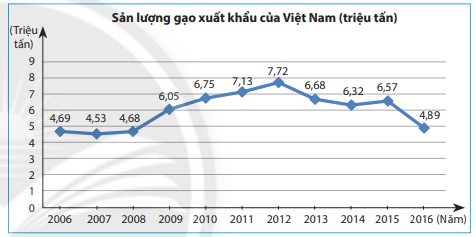
a) Đơn vị thời gian là gì?

b) Năm nào có sản lượng gạo xuất khẩu cao nhất?

c) Năm nào có sản lượng gạo xuất khẩu thấp nhất?

d) Sản lượng gạo xuất khẩu tăng trong khoảng thời gian nào?

e) Sản lượng gạo xuất khẩu giảm trong khoảng thời gian nào?

Phương pháp giải:

Quan sát đường gấp khúc từ trái qua phải

Đọc số liệu được ghi trên các điểm có đánh dấu

Lời giải:

a) Đơn vị thời gian là: Năm

b) Năm 2012 có sản lượng gạo xuất khẩu cao nhất

c) Năm 2007 có sản lượng gạo xuất khẩu thấp nhất

d) Sản lượng gạo xuất khẩu tăng trong khoảng thời gian từ 2007 – 2008; 2008 – 2009 ; 2009 – 2010; 2010 – 2011; 2011 – 2012; 2014 – 2015

e) Sản lượng gạo xuất khẩu giảm trong khoảng thời gian từ 2006 – 2007; 2002 – 2013; 2013 – 2014 ;2015 – 2016

Xem thêm các bài giải SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết:

Bài 3: Biểu đồ đoạn thẳng

Bài 1: Tỉ lệ thức – Dãy tỉ số bằng nhau

Bài 2: Đại lượng tỉ lệ thuận

Bài 3: Đại lượng tỉ lệ nghịch

Sách bài tập Toán 7 Bài tập cuối chương 5 (Chân trời sáng tạo)

Giải SBT Toán lớp 7 Bài tập cuối chương 5

Giải trang 114 Tập 1

Bài 1 trang 114 Sách bài tập Toán 7 Tập 1: Tìm hiểu về khả năng tự nấu cơm của các bạn học sinh lớp 7C được cho bởi bảng thống kê sau:

Khả năng tự nấu cơm	Không đạt	Đạt	Giỏi	Xuất sắc
Số bạn tự đánh giá	20	10	6	4

a) Hãy phân loại dữ liệu trong bảng thống kê trên dựa trên tiêu chí định tính và định lượng.

b) Tính sĩ số của lớp.

Lời giải

a) Dữ liệu định tính là dữ liệu được biểu diễn bằng từ, chữ cái, kí hiệu, tên gọi,…

Dữ liệu định lượng là dữ liệu được biểu diễn bằng số thực.

Vậy dữ liệu định tính trong bảng thống kê là khả năng tự nấu cơm của các bạn học sinh: không đạt, đạt, giỏi, xuất sắc.

Dữ liệu định lượng trong bảng thống kê là số bạn tự đánh giá: 20, 10, 6, 4.

b) Tổng số bạn học sinh tự đánh giá là:

20 + 10 + 6 + 4 = 40 (bạn).

Vậy sĩ số của lớp 7C là 40 bạn.

Bài 2 trang 114 Sách bài tập Toán 7 Tập 1: Tìm hiểu về sở thích đối với môn bóng chuyền của các bạn học sinh lớp 7C được cho bởi bảng thống kê sau:

Thái độ	Không thích	Không quan tâm	Thích	Rất thích
Số bạn nữ	20	10	6	4

Dữ liệu trên có đại diện được cho thái độ đối với môn bóng đá của tất cả học sinh lớp 7C hay không?

Lời giải

Bài 3 trang 114 Sách bài tập Toán 7 Tập 1: Vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu của bảng thống kê sau:

Số học sinh đạt điểm giỏi môn Văn trong 4 tháng học kì I của khối lớp 7
Tháng	Số học sinh
9	15
10	24
11	20
12	36

Lời giải

Để vẽ biểu đồ đoạn thẳng biểu diễn số liệu thống kê số học sinh đạt điểm giỏi môn Văn trong 4 tháng học kì I của khối lớp 7, ta thực hiện các bước sau:

Bước 1: Vẽ hai trục ngang và thẳng đứng vuông góc với nhau.

– Trục ngang: Ghi các mốc thời gian (tháng: 9, 10, 11, 12).

– Trục thẳng đứng: Chọn khoảng chia thích hợp với số liệu và ghi số ở các vạch chia.

Ở đây ta có thể chọn khoảng chia là 5.

Bước 2:

– Tại mốc tháng 9 trên trục ngang, đánh dấu một điểm cách điểm mốc thời gian theo chiều thẳng đứng một khoảng 15 tại mốc thời gian đó, tương ứng với khoảng chia trên trục thẳng đứng.

Tương tự như vậy với tại các mốc thời gian còn lại.

– Vẽ các đoạn thẳng nối từng cặp điểm tương ứng với cặp mốc thời gian liên tiếp, ta được một đường gấp khúc biểu diễn sự thay đổi của số liệu theo thời gian.

Bước 3: Hoàn thiện biểu đồ.

– Ghi tên cho biểu đồ: Số học sinh đạt điểm giỏi môn Văn trong 4 tháng học kì I của khối lớp 7.

– Ghi chú các giá trị số liệu tại các đầu đoạn thẳng.

– Ghi đơn vị trên hai trục.

Ta có biểu đồ sau:

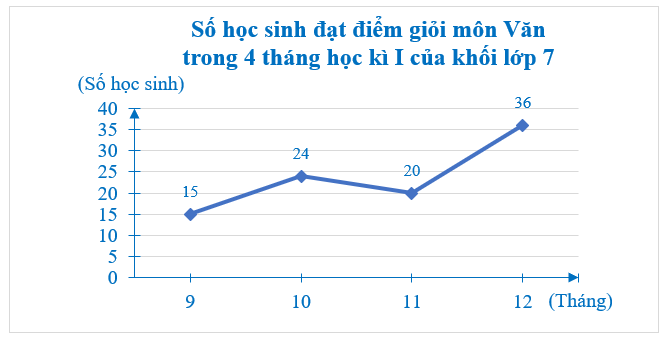
Sách bài tập Toán 7 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

Giải trang 115 Tập 1

Bài 4 trang 115 Sách bài tập Toán 7 Tập 1: Hãy đọc dữ liệu được biểu diễn trong biểu đồ đoạn thẳng sau và ghi vào bảng thống kê tương ứng.

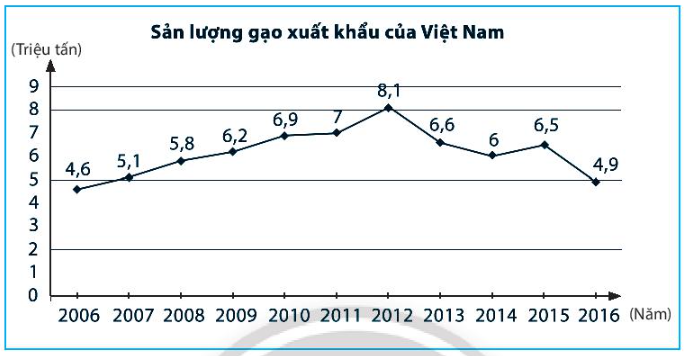
Sách bài tập Toán 7 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

(Nguồn: Niên giám thống kê 2020)

Lời giải

Quan sát biểu đồ đoạn thẳng ở trên ta thấy:

– Biểu đồ biểu diễn các thông tin về sản lượng gạo xuất khẩu của Việt Nam (triệu tấn).

– Đơn vị thời gian là năm.

– Sản lượng gạo xuất khẩu của Việt Nam qua các năm:

+ Sản lượng gạo xuất khẩu của Việt Nam năm 2006 là 4,6 (triệu tấn).

+ Tương tự như vậy ta đọc được sản lượng gạo xuất khẩu của Việt Nam qua các năm còn lại.

Ta có bảng thống kê sau:

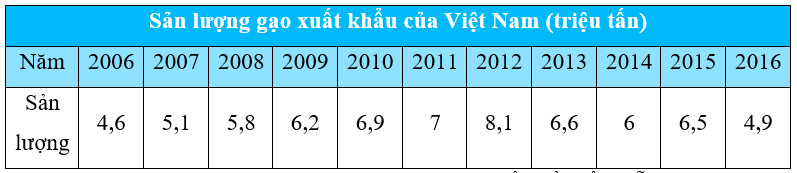
Sách bài tập Toán 7 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

Bài 5 trang 115 Sách bài tập Toán 7 Tập 1: Vẽ biểu đồ biểu diễn dữ liệu trong bảng thống kê sau:

Tổ	Số lượng điểm khá, giỏi môn Toán của tổ	Tỉ lệ phần trăm điểm khá, giỏi của mỗi tổ so với cả lớp
1	28	31%
2	34	38%
3	28	31%
Tổng	90	100%

Lời giải

Để vẽ biểu đồ hình quạt tròn biểu diễn dữ liệu như sau:

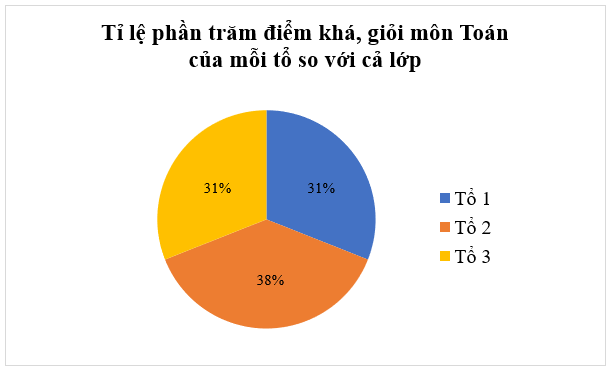
– Ghi tên biểu đồ: Tỉ lệ phần trăm điểm khá, giỏi môn Toán của mỗi tổ so với cả lớp.

– Ghi chú tên các đối tượng và các tỉ lệ phần trăm trên biểu đồ.

Tổ 1: 31%; Tổ 2: 38%; Tổ 3: 31%.

Ta có biểu đồ như sau:

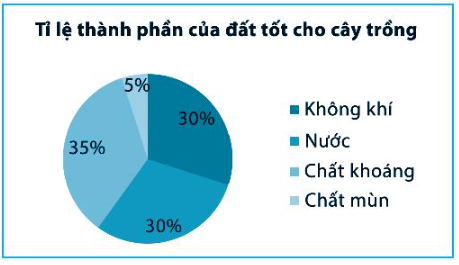
Sách bài tập Toán 7 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

Bài 6 trang 115 Sách bài tập Toán 7 Tập 1: Đọc các thông tin được ghi trong biểu đồ hình quạt tròn sau và lập bảng thống kê tương ứng.

Sách bài tập Toán 7 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

Lời giải

Quan sát biểu đồ hình quạt tròn ở trên ta thấy:

– Có bốn thành phần của đất tốt cho cây trồng được biểu thị bằng bốn hình quạt có trong hình tròn là: Không khí, Nước, Chất khoáng, Chất mùn.

– Tỉ lệ phần trăm của từng thành phần là:

+ Tỉ lệ phần trăm của Không khí chiếm: 30%;

+ Tỉ lệ phần trăm của Nước chiếm: 30%;

+ Tỉ lệ phần trăm của Chất khoáng chiếm: 35%;

+ Tỉ lệ phần trăm của Chất mùn chiếm: 5%;

Ta có bảng thống kê sau:

Tỉ lệ thành phần của đất tốt cho cây trồng
Thành phần	Không khí	Nước	Chất khoáng	Chất mùn
Tỉ lệ	30%	30%	35%	5%

Giải trang 116 Tập 1

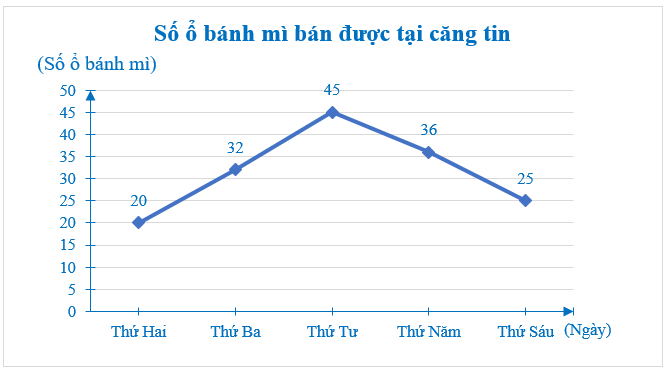
Bài 7 trang 116 Sách bài tập Toán 7 Tập 1: Bảng dữ liệu sau cho biết số ổ bánh mì bán được tại căng tin trường Trung học cơ sở Quang Trung vào các ngày trong tuần vừa qua. Em hãy vẽ biểu đồ đoạn thẳng biểu diễn bảng dữ liệu này.

Ngày	Số ổ bánh mì bán được tại căng tin
Thứ Hai	20
Thứ Ba	32
Thứ Tư	45
Thứ Năm	36
Thứ Sáu	25

Lời giải

Để vẽ biểu đồ đoạn thẳng biểu diễn số liệu thống kê số ổ bánh mì bán được tại căng tin, ta thực hiện các bước sau:

Bước 1: Vẽ hai trục ngang và thẳng đứng vuông góc với nhau.

– Trục ngang: Ghi các mốc thời gian (Thứ Hai, Thứ Ba, Thứ Tư, Thứ Năm, Thứ Sáu).

– Trục thẳng đứng: Chọn khoảng chia thích hợp với số liệu và ghi số ở các vạch chia.

Ở đây ta có thể chọn khoảng chia là 5.

Bước 2:

– Tại mốc Thứ Hai trên trục ngang, đánh dấu một điểm cách điểm mốc thời gian theo chiều thẳng đứng một khoảng 20 tại mốc thời gian đó, tương ứng với khoảng chia trên trục thẳng đứng.

Tương tự như vậy với tại các mốc thời gian còn lại.

Bước 3: Hoàn thiện biểu đồ.

– Ghi tên cho biểu đồ: Số ổ bánh mì bán được tại căng tin.

– Ghi chú các giá trị số liệu tại các đầu đoạn thẳng.

– Ghi đơn vị trên hai trục.

Ta có biểu đồ sau:

Sách bài tập Toán 7 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

Bài 8 trang 116 Sách bài tập Toán 7 Tập 1: Hãy phân tích biểu đồ đoạn thẳng sau:

Sách bài tập Toán 7 Bài tập cuối chương 5 - Chân trời sáng tạo (ảnh 1)

(Nguồn: https://kenhthoitiet.vn/)

Lời giải

Phân tích biểu đồ trên ta nhận thấy:

– Biểu đồ biểu diễn nhiệt độ trung bình của mỗi tháng trong năm 2021 tại thành phố Đà Lạt.

– Đơn vị thời gian là tháng.

– Tháng 4 có nhiệt độ trung bình cao nhất (19,1 °C).

– Tháng 12 có nhiệt độ trung bình thấp nhất (15,7 °C).

– Nhiệt độ trung bình tăng từ tháng 1 đến tháng 4 (từ 16,1 °C lên 19,1 °C) và từ tháng 8 đến tháng 9 (từ 18,2 °C lên 18,7 °C).

– Nhiệt độ trung bình giảm từ tháng 4 đến tháng 8 (từ 19,1 °C xuống 18,2 °C) và từ tháng 9 đến tháng 12 (từ 18,7 °C xuống 15,7 °C).

Xem thêm các bài giải SBT Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 3 : Biểu đồ đoạn thẳng

Bài tập cuối chương 5

Bài 1 : Tỉ lệ thức – Dãy tỉ số bằng nhau

Bài 2 : Đại lượng tỉ lệ thuận

Bài 3 : Đại lượng tỉ lệ nghịch

Vở thực hành Toán 7 Bài 4 (Chân trời sáng tạo): Bài tập cuối chương 5

Giải VTH Toán lớp 7 Bài 4: Bài tập cuối chương 5

Câu 1 trang 79 vở thực hành Toán 7 Tập 1: Cho các dãy dữ liệu sau:

(1) Các món ăn sáng ngon

(2) Loại phim mà em yêu thích

(3) Giá tiền các loại trà sữa

(4) Đánh giá về một bài hát

Trong các dãy dữ liệu trên, có bao nhiêu dữ liệu định tính ?

A. 1;

B. 2;

C. 3;

D. 4.

Lời giải:

Đáp án đúng là: C

Dữ liệu (1) có thể được biểu diễn bằng từ, chữ cái, kí hiệu nên nó là dữ liệu định tính.

Dữ liệu (2) có thể được biểu diễn bằng từ, chữ cái, kí hiệu nên nó là dữ liệu định tính.

Dữ liệu (3) được biểu diễn bằng số thực nên nó là dữ liệu định lượng.

Dữ liệu (4) có thể được biểu diễn bằng từ, chữ cái, kí hiệu nên nó là dữ liệu định tính.

Vậy có 3 dữ liệu định tính là (1), (2), (4).

Biểu đồ sau cho thông tin về môn thể thao luyện tập hàng ngày của học sinh khối lớp 7. Quan sát biểu đồ và trả lời các câu hỏi B2 – B3.

Câu 2 trang 80 vở thực hành Toán 7 Tập 1: Biết môn cầu lông có số người chọn nhiều gấp 3 môn bơi. Hỏi môn cầu lông có bao nhiêu phần trăm các bạn lựa chọn ?

A. 24%;

B. 28%;

C. 36%;

D. 40%.

Lời giải:

Đáp án đúng là: C

Tổng số phần trăm số người chọn môn bơi và môn cầu lông là:

100% – (8% + 27% + 17%) = 48%.

Gọi môn bơi có tỉ lệ người chọn là x% (x > 0) thì môn cầu lông có tỉ lệ người chọn là 3x%.

Do đó, ta có: x + 3x = 48 hay x = 12.

Vậy môn cầu lông có 36% người chọn.

Câu 3 trang 80 vở thực hành Toán 7 Tập 1: Biết có 34 học sinh lựa chọn môn chạy. Hỏi có bao nhiêu học sinh đã tham gia khảo sát.

A. 160;

B. 200;

C. 280;

D. 320.

Lời giải:

Đáp án đúng là: B

Tỉ lệ số học sinh lựa chọn môn chạy là 17% ứng với 34 bạn. Vậy số học sinh đã tham gia khảo sát là: 34 : 17% = 200 (bạn).

Quan sát biểu đồ và trả lời các câu hỏi B4 – B6.

Câu 4 trang 80 vở thực hành Toán 7 Tập 1: Lượng truy cập vào website chênh lệch giữa ngày thứ Năm và Chủ nhật là bao nhiêu người ?

A. 121;

B. 176;

C. 142;

D. 118.

Lời giải:

Đáp án đúng là: B

Lượng truy cập vào website vào ngày thứ Năm là 148 người.

Lượng truy cập vào website vào ngày Chủ nhật là 324 người.

Lượng truy cập vào website chênh lệch giữa ngày thứ Năm và Chủ nhật là:

324 – 148 = 176 (người).

Câu 5 trang 80 vở thực hành Toán 7 Tập 1: Vào thứ Bảy, lượng học sinh truy cập vào website giảm 30% so với thứ Ba. Có bao nhiêu học sinh truy cập website vào thứ Bảy?

A. 148;

B. 154;

C. 161;

D. 175.

Lời giải:

Đáp án đúng là: C

Vào thứ Bảy, lượng học sinh truy cập vào website giảm 30% so với thứ Ba. Do đó số lượng học sinh truy cập vào website vào thứ Bảy bằng 70% so với thứ Ba.

Số học sinh truy cập website vào thứ Bảy là: 230 . 70% = 161 (bạn).

Câu 6 trang 80 vở thực hành Toán 7 Tập 1: Hỏi trung bình cả tuần có bao nhiêu học sinh truy cập vào website?

A. 148;

B. 154;

C. 161;

D. 212.

Lời giải:

Đáp án đúng là: D

Tổng số học sinh truy cập vào website trong cả tuần là:

182 + 230 + 206 + 148 + 233 + 161 + 324 = 1 484 (bạn)

Vậy trung bình cả tuần có số học sinh truy cập vào website là:

1 484 : 7 = 212 (bạn).

Câu 7 trang 81 vở thực hành Toán 7 Tập 1: Xin ý kiến 40 học sinh lớp 7A về việc chọn màu áo cho đội tuyển thể thao của lớp, kết quả có trong bảng dữ liệu sau:

Biểu đồ hình quạt tròn nào dưới đây là phù hợp nhất với dữ liệu trên ?

A.

B.

C.

D.

Lời giải:

Đáp án đúng là: D

Từ bảng dữ liệu ta có bảng thống kê tỉ lệ như sau:

Màu

Xanh

Đỏ

Vàng

Đen

Trắng

Số bạn chọn

15%

25%

35%

15%

10%

Dựa vào bảng thống kê tỉ lệ, ta thấy biểu đồ hình quạt tròn dưới đây là phù hợp nhất với dữ liệu trên

Với thứ tự biểu diễn lần lượt theo chiều kim đồng hồ là: Xanh, Vàng, Đỏ, Trắng, Đen.

Bài 1 trang 81 vở thực hành Toán 7 Tập 1: Xác định phương pháp thu thập dữ liệu trong mỗi trường hợp sau và cho biết mỗi dữ liệu thu được thuộc loại nào ?

a) Thể loại phim yêu thích của các bạn cùng lớp.

b) Kết quả đánh giá rèn luyện học kì 1 của các bạn cùng tổ.

c) Số học sinh nghỉ học trong tuần của lớp.

Lời giải:

a) Thu thập dữ liệu “Thể loại phim yêu thích của các bạn cùng lớp” bằng phương pháp phỏng vấn hoặc lập bảng hỏi.

Dữ liệu thu được có thể biểu diễn bằng từ, chữ cái, kí hiệu nên nó là dữ liệu định tính.

b) Thu thập dữ liệu “Kết quả đánh giá rèn luyện học kì 1 của các bạn cùng tổ” bằng phương pháp phỏng vấn hoặc hỏi giáo viên chủ nhiệm.

Dữ liệu thu được có thể biểu diễn bằng từ, chữ cái, kí hiệu nên nó là dữ liệu định tính.

c) Thu thập dữ liệu “Số học sinh nghỉ học trong tuần của lớp” bằng phương pháp quan sát.

Dữ liệu thu được biểu diễn bằng số thực nên nó là dữ liệu định lượng.

Bài 2 trang 81 vở thực hành Toán 7 Tập 1: Biểu đồ sau cho biết tỉ lệ học sinh các khối lớp trong danh sách 25 cầu thủ đội dự tuyển bóng đá của trường.

a) Trong đội dự tuyển, khối lớp nào có ít thành viên nhất và có bao nhiêu cầu thủ ?

b) Hai khối lớp nào có số thành viên trong đội dự tuyển bằng nhau ? Mỗi khối lớp có bao nhiêu cầu thủ.

c) Trong đội dự tuyển, khối lớp 7 có ít hơn khối lớp 8 bao nhiêu cầu thủ ?

Lời giải:

a) Khối có ít thành viên nhất là khối 6 với 25 . 12% = 3 cầu thủ.

b) Hai khối lớp có số thành viên bằng nhau là khối 8 và khối 9

Mỗi khối có 25.32% = 8 cầu thủ.

c) Trong đội dự tuyển, khối lớp 7 có ít hơn khối lớp 8 số cầu thủ là: 8 – 25 . 24% = 8 – 6 = 2 cầu thủ.

Bài 3 trang 82 vở thực hành Toán 7 Tập 1: Khảo sát về môn học yêu thích từ 575 học sinh lớp 7, dữ liệu được cho trong biểu đồ sau:

a) Tìm giá trị của a.

b) Trong số các học sinh được hỏi, có bao nhiêu bạn thích học môn Toán ?

c) Trong số các học sinh được hỏi, có bao nhiêu bạn thích học các môn tích hợp (Khoa học tự nhiên, Lịch sử và Địa lí, Nghệ thuật).

Lời giải:

a) Ta có: 28 + 5a + 7a + 24 + 8 + 4 = 100 (%). Vậy a = 3.

b) Số bạn thích học môn Toán là: 575 . 28% = 161 (bạn).

c) Số bạn thích học các môn tích hợp là: 575 . [(5 . 3)% + (7 . 3)% + 8%) = 253 (bạn).

Bài 4 trang 82 vở thực hành Toán 7 Tập 1: Hai biểu đồ sau cho kết quả xếp loại rèn luyện học kì 1 của hai lớp 7A và 7B:

a) Có ý kiến nói rằng số học sinh xếp loại Khá ở hai lớp bằng nhau. Ý kiến này có đúng không ? Tại sao ?

b) Biết lớp 7A có 40 học sinh, lớp 7B có 45 học sinh. Hỏi cả hai lớp có tất cả bao nhiêu học sinh được xếp loại Tốt.

Lời giải:

a) Ý kiến này chưa chắc đúng vì nếu số học sinh của hai lớp khác nhau thì số học sinh được xếp loại Khá sẽ khác nhau dù có tỉ lệ giống nhau.

b) Cả hai lớp có số học sinh được xếp loại Tốt là:

40 . 65% + 45 . 60% = 26 + 27 = 53 (bạn).

Bài 5 trang 83 vở thực hành Toán 7 Tập 1: Biểu đồ dưới đây cho biết chuẩn chiều cao của nữ theo độ tuổi:

a) Đến tuổi nào, chuẩn chiều cao của nữ đã vượt mức 151 cm.

b) Theo chuẩn trên, trong khoảng độ tuổi nào, chiều cao tăng nhanh nhất.

c) Với xu thế tăng chiều cao ổn định như các độ tuổi trước, chuẩn chiều cao năm 17 tuổi có thể đưa ra mức 170 cm được không ?

Lời giải:

a) Chuẩn chiều cao của nữ vượt mức 151 cm năm 12 tuổi.

b) Chiều cao tăng nhanh nhất trong độ tuổi 10 – 11 (tăng 6,5 cm).

c) Với xu thế tăng chiều cao ổn định như các độ tuổi trước, chuẩn chiều cao tăng chậm dần theo độ tuổi tăng dần, do đó, chuẩn chiều cao năm 17 tuổi không thể đưa ra mức 170 cm.

Bài 6 trang 83 vở thực hành Toán 7 Tập 1: Biểu đồ dưới đây cho biết nhiệt độ trung bình tại Thủ đô Hà Nội và Thành phố Quy Nhơn (tỉnh Bình Định) trong 6 tháng đầu năm 2022:

a) Có bao nhiêu tháng nhiệt độ trung bình tại Quy Nhơn thấp hơn Hà Nội ?

b) Mức chênh lệch cao nhất về nhiệt độ trung bình giữa hai thành phố là bao nhiêu độ và xảy ra vào tháng nào ?

Lời giải:

a) Nhiệt độ trung bình tại Quy Nhơn thấp hơn Hà Nội trong 2 tháng. (tháng 5 và tháng 6)

b) Mức chênh lệch cao nhất về nhiệt độ là 7,1°C ở tháng 3.

Bài 7 trang 84 vở thực hành Toán 7 Tập 1: Một khảo sát về số người nghe đài (làm tròn số) vào buổi tối có kết quả sau:

• Lúc 19 giờ có khoảng 300 người nghe đài.

• Đến 20 giờ, số người nghe đã tăng lên 50% so với lúc 19 giờ.

• Tỉ số người nghe lúc 20 giờ và 21 giờ là 9 : 10.

• Đến 22 giờ, số người nghe giảm 20% so với lúc 21 giờ.

• Tính trung bình, từ 19 giờ đến 23 giờ có 380 người nghe đài.

a) Lập bảng thống kê số lượng người nghe đài tại từng thời điểm.

b) Vẽ biểu đồ đoạn thẳng biểu diễn dữ liệu đã cho.

Lời giải:

a) Thời điểm 20 giờ có số người nghe đài là: 300 + 300 . 50% = 450 (người).

Thời điểm 21 giờ có số người nghe đài là: 450 . 10 : 9 = 500 (người).

Thời điểm 22 giờ có số người nghe đài là: 500 – 500 . 20% = 400 (người).

Thời điểm 23 giờ có số người nghe đài là: 380 . 5 – (300 + 450 + 500 + 400) = 250 (người).

Bảng thống kê:

Thời điểm

19 giờ

20 giờ

21 giờ

22 giờ

23 giờ

Số người

300

450

500

400

250

b) Biểu đồ đoạn thẳng
Sách bài tập Toán 6 (Cánh diều): Bài tập cuối chương 5 trang 59, 60, 61, 62

Giải SBT Toán lớp 6 Bài tập cuối chương 5 trang 59, 60, 61, 62

Bài 121 trang 59 sách bài tập Toán lớp 6 Tập 2: Viết các số sau theo thứ tự tăng dần:

a) $\frac{- 5}{16}; \frac{- 17}{8}; \frac{17}{21}; \frac{- 11}{32}; \frac{35}{42}; \frac{71}{62}$ ;

b) –1,002; 1,01; –3,761; –6,2314; 0,001; 7,5.

Lời giải:

a) $\frac{- 5}{16}; \frac{- 17}{8}; \frac{17}{21}; \frac{- 11}{32}; \frac{35}{42}; \frac{71}{62}$

Ta chia các phân số trên thành 2 nhóm:

• Nhóm 1: gồm các phân số âm $\frac{- 5}{16}; \frac{- 17}{8}; \frac{- 11}{32}$ ;

• Nhóm 2: gồm các phân số dương $\frac{17}{21}; \frac{35}{42}; \frac{71}{62}$ .

+ So sánh nhóm 1: $\frac{- 5}{16}; \frac{- 17}{8}; \frac{- 11}{32}$

Ta có $\frac{- 17}{8} = \frac{(- 17) .4}{8.4} = \frac{- 68}{32}$ và $\frac{- 5}{16} = \frac{(- 5) .2}{16.2} = \frac{- 10}{32}$ .

Vì –68 < –11 < –10 nên $\frac{- 68}{32} < \frac{- 11}{32} < \frac{- 10}{32}$ .

Khi đó $\frac{- 17}{8} < \frac{- 11}{32} < \frac{- 5}{16}$ .

+ So sánh nhóm 2: $\frac{17}{21}; \frac{35}{42}; \frac{71}{62}$

Ta có $\frac{17}{21} = \frac{17.2}{21.2} = \frac{34}{42}$ ; giữ nguyên $\frac{35}{42}$ .

Vì 34 < 35 nên $\frac{34}{42} < \frac{35}{42}$ .

Khi đó $\frac{17}{21} < \frac{35}{42}$

Lại có $\frac{35}{42} < 1 < \frac{71}{62}$

Nên $\frac{17}{21} < \frac{35}{42} < \frac{71}{62}$ .

Ta đã biết phân số âm luôn nhỏ hơn phân số dương nên ta có:

$\frac{- 17}{8} < \frac{- 11}{32} < \frac{- 5}{16} < \frac{17}{21} < \frac{35}{42} < \frac{71}{62}$ .

Vậy sắp xếp theo thứ tự tăng dần là: $\frac{- 17}{8}; \frac{- 11}{32}; \frac{- 5}{16}; \frac{17}{21}; \frac{35}{42}; \frac{71}{62}$ .

b) –1,002; 1,01; –3,761; –6,2314; 0,001; 7,5.

Ta chia các số thập phân trên thành 2 nhóm:

• Nhóm 1: gồm các số thập phân âm –1,002; –3,761; –6,2314;

• Nhóm 2: gồm các số thập phân dương 1,01; 0,001; 7,5.

+ So sánh nhóm 1: –1,002; –3,761; –6,2314;

Xét các số thập phân 1,002; 3,761; 6,2314.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng đơn vị. Do 6 > 3 > 1 nên 6,2314 > 3,761 > 1,002.

Do đó –6,2314 < –3,761 < –1,002.

+ So sánh nhóm 2: 1,01; 0,001; 7,5.

Kể từ trái sang phải, cặp chữ số cùng hàng đầu tiên khác nhau là cặp chữ số ở vị trí hàng đơn vị. Do 0 < 1 < 7 nên 0,001 < 1,01 < 7,5.

Ta đã biết các số thập phân âm luôn nhỏ hơ các số thập phân dương nên ta có:

–6,2314 < –3,761 < –1,002 < 0,001 < 1,01 < 7,5.

Vậy sắp xếp theo thứ tự tăng dần là: –6,2314; –3,761; –1,002; 0,001; 1,01; 7,5.

Bài 122 trang 59 sách bài tập Toán lớp 6 Tập 2: Thực hiện phép tính:

a) 0,58.7² – (–7).(–0,7).15,8;

b) 0,05 : 0,5 + 7 : 0,7 + 0,9 : 0,009;

c) $\frac{9}{11} . \frac{92}{121} + \frac{2}{- 121} . \frac{9}{11} + \frac{31}{121} . \frac{9}{11}$ ;

d) $\frac{20 212 021}{2 021} . \frac{2 020}{20 202 020} . \frac{2^{3}}{3^{2}} . \frac{- 3}{2^{2}}$ .

Lời giải:

a) 0,58.7² – (–7).(–0,7).15,8

= 0,58.49 – 7.7.1,58

= 0,58.49 – 49.1,58

= 49.(0,58 – 1,58)

= 49.(–1)

= –49.

b) 0,05 : 0,5 + 7 : 0,7 + 0,9 : 0,009

= 0,1 + 10 + 100

= 110,1.

c) $\frac{9}{11} . \frac{92}{121} + \frac{2}{- 121} . \frac{9}{11} + \frac{31}{121} . \frac{9}{11}$

$= \frac{9}{11} . \frac{92}{121} - \frac{9}{11} . \frac{2}{121} + \frac{9}{11} . \frac{31}{121}$

$= \frac{9}{11} . (\frac{92}{121} - \frac{2}{121} + \frac{31}{121})$

$= \frac{9}{11} . \frac{121}{121} = \frac{9}{11} .1 = \frac{9}{11}$ .

d) $\frac{20 212 021}{2 021} . \frac{2 020}{20 202 020} . \frac{2^{3}}{3^{2}} . \frac{- 3}{2^{2}}$

$= \frac{2 021 . 10 001}{2 021} . \frac{2 020}{2 020 . 10 001} . \frac{2^{2} .2}{3.3} . \frac{(- 1) .3}{2^{2}}$

$= \frac{- 2}{3}$ .

Bài 123 trang 60 sách bài tập Toán lớp 6 Tập 2: Tính một cách hợp lí:

a) 1,6 + (2,7 – 0,7.6) – (94.0,7 – 99.2,7);

b) 0,1 – 0,02 + 0,2 – 0,01 + 0,03 – 0,8;

c) $(\frac{- 5}{116} + \frac{- 117}{232} - \frac{71}{464}) . (\frac{5}{6} - \frac{1}{2} - \frac{1}{3})$ ;

d) $(\frac{2}{1.3} + \frac{2}{3.5} + \frac{2}{5.7}) . (\frac{10.13}{3} - \frac{2^{2}}{3} - \frac{5^{3}}{3})$ ;

e) $\frac{2.4.10 + 4.6.8 + 14.16.20}{3.6.15 + 6.9.12 + 21.24.30}$ .

Lời giải:

a) 1,6 + (2,7 – 0,7.6) – (94.0,7 – 99.2,7)

= 1,6 + 2,7 – 0,7.6 – 94.0,7 + 99.2,7

= 1,6 + 2,7.(1 + 99) – 0,7.(6 + 94)

= 1,6 + 2,7.100 – 0,7.100

= 1,6 + 270 – 70 = 201,6.

b) 0,1 – 0,02 + 0,2 – 0,01 + 0,03 – 0,8

= 0,1 + 0,2 + (–0,01 – 0,02 + 0,03) – 0,8

= 0,3 + 0 – 0,8

= –0,5.

c) $(\frac{- 5}{116} + \frac{- 117}{232} - \frac{71}{464}) . (\frac{5}{6} - \frac{1}{2} - \frac{1}{3})$

$= (\frac{- 5}{116} + \frac{- 117}{232} - \frac{71}{464}) . (\frac{5}{6} - \frac{3}{6} - \frac{2}{6})$

$= (\frac{- 5}{116} + \frac{- 117}{232} - \frac{71}{464}) .0 = 0$ .

d) $(\frac{2}{1.3} + \frac{2}{3.5} + \frac{2}{5.7}) . (\frac{10.13}{3} - \frac{2^{2}}{3} - \frac{5^{3}}{3})$

$= (1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + \frac{1}{5} - \frac{1}{7}) . (\frac{130}{3} - \frac{4}{3} - \frac{125}{3})$

$= (1 - \frac{1}{7}) . \frac{1}{3} = \frac{6}{7} . \frac{1}{3} = \frac{2}{7}$ .

e) $\frac{2.4.10 + 4.6.8 + 14.16.20}{3.6.15 + 6.9.12 + 21.24.30}$

$= \frac{2.4.2.5 + 4.6.2.2.2 + 7.2.4.4.2.10}{3.6.3.5 + 6.3.3.2.6 + 3.7.6.4.3.10}$

$= \frac{2.4.2. (5 + 2.6 + 7.4.10)}{3.6.3. (5 + 2.6 + 7.4.10)}$

$= \frac{2.4.2}{3.2.3.3} = \frac{2.4}{3.3.3} = \frac{8}{27}$ .

Bài 124 trang 60 sách bài tập Toán lớp 6 Tập 2: Tìm x, biết:

a) –3x + 7 = 12 – 125;

b) $\frac{1}{3} : (2 x - 1) = \frac{- 4}{21}$ ;

c) [124 – (20 – 4x)] : 20 = 12;

d) $(\frac{1}{2.3} + \frac{1}{3.4} + … + \frac{1}{8.9} + \frac{1}{9.10}) . x = \frac{1}{5}$ .

Lời giải:

a) –3x + 7 = 12 – 125

–3x + 7 = –113

–3x = –113 – 7

–3x = –120

x = (–120) : (–3) = 40.

Vậy x = 40.

b) $\frac{1}{3} : (2 x - 1) = \frac{- 4}{21}$

$2 x - 1 = \frac{1}{3} : (\frac{- 4}{21})$

$2 x - 1 = \frac{1}{3} . \frac{- 21}{4} = \frac{- 7}{4}$

$2 x = \frac{- 7}{4} + 1 = \frac{- 3}{4}$

$x = \frac{- 3}{4} : 2 = \frac{- 3}{8}$ .

Vậy $x = \frac{- 3}{8}$ .

c) [124 – (20 – 4x)] : 20 = 12

124 – (20 – 4x) = 12.20

124 – (20 – 4x) = 240

20 – 4x = 124 – 240

20 – 4x = –116

4x = 20 – (–116)

4x = 136

x = 136 : 4

x = 34.

Vậy x = 34.

d) $(\frac{1}{2.3} + \frac{1}{3.4} + … + \frac{1}{8.9} + \frac{1}{9.10}) . x = \frac{1}{5}$

$(\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + … + \frac{1}{8} - \frac{1}{9} + \frac{1}{9} - \frac{1}{10}) . x = \frac{1}{5}$

$(\frac{1}{2} - \frac{1}{10}) . x = \frac{1}{5}$

$(\frac{5}{10} - \frac{1}{10}) . x = \frac{1}{5}$

$\frac{4}{10} . x = \frac{1}{5}$

$\frac{2}{5} . x = \frac{1}{5}$

$x = \frac{1}{5} : \frac{2}{5}$

$x = \frac{1}{5} . \frac{5}{2} = \frac{1}{2}$

Vậy $x = \frac{1}{2}$ .

Bài 125 trang 60 sách bài tập Toán lớp 6 Tập 2: Tìm các số nguyên x sao cho:

a) $\frac{- 2}{5} < \frac{x}{15} < \frac{1}{6}$ ;

b) $\frac{1}{2} + \frac{1}{3} - \frac{5}{12} < 2 x < \frac{- 12}{31} + \frac{- 136}{- 31}$ .

Lời giải:

a) Ta có:

⦁ $\frac{- 2}{5} = \frac{(- 2) .6}{5.6} = \frac{- 12}{30}$ ;

⦁ $\frac{x}{15} = \frac{2 x}{2.15} = \frac{2 x}{30}$ ;

⦁ $\frac{1}{6} = \frac{1.5}{6.5} = \frac{5}{30}$ .

Vì $\frac{- 2}{5} < \frac{x}{15} < \frac{1}{6}$ nên $\frac{- 12}{30} < \frac{2 x}{30} < \frac{5}{30}$ .

Do đó –12 < 2x < 5.

Suy ra –6 < x < 2,5.

Mà x là số nguyên nên x ∈ {–5; –4; –3; –2; –1; 0; 1; 2}.

Vậy x ∈ {–5; –4; –3; –2; –1; 0; 1; 2}.

b) Ta có:

⦁ $\frac{1}{2} + \frac{1}{3} - \frac{5}{12} = \frac{6}{12} + \frac{4}{12} - \frac{5}{12} = \frac{5}{12}$ ;

⦁ $\frac{- 12}{31} + \frac{- 136}{- 31} = \frac{- 12}{31} + \frac{136}{31} = \frac{124}{31} = 4$

Vì $\frac{1}{2} + \frac{1}{3} - \frac{5}{12} < 2 x < \frac{- 12}{31} + \frac{- 136}{- 31}$ nên $\frac{5}{12} < 2 x < 4$

Do đó $\frac{5}{24} < x < 2$ .

Mà x là số nguyên nên x = 1.

Vậy x = 1.

Bài 126 trang 60 sách bài tập Toán lớp 6 Tập 2: So sánh:

a) $A = \frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + … + \frac{1}{2^{2 020}} + \frac{1}{2^{2 021}}$ và $B = \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{13}{60}$ ;

b) $C = \frac{2 019}{2 020} . \frac{2 021}{2 022}$ và $D = \frac{2 020 + 2 022}{2 019 + 2 021} . \frac{3}{2}$ .

Lời giải:

a) Ta có:

$2 A = 2. (\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + … + \frac{1}{2^{2 020}} + \frac{1}{2^{2 021}})$

$2 A = 1 + \frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + … + \frac{1}{2^{2 019}} + \frac{1}{2^{2 020}}$

Suy ra: $2 A - A = (1 + \frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + … + \frac{1}{2^{2 019}} + \frac{1}{2^{2 020}})$

$- (\frac{1}{2} + \frac{1}{2^{2}} + \frac{1}{2^{3}} + … + \frac{1}{2^{2 020}} + \frac{1}{2^{2 021}})$

Do đó $A = 1 - \frac{1}{2^{2021}} < 1$ .

Lại có $B = \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{13}{60} = \frac{20 + 15 + 12 + 13}{60} = \frac{60}{60} = 1$ .

Vậy A < B.

b) Ta có $0 < \frac{2 019}{2 020} < 1$ và $0 < \frac{2 021}{2 022} < 1$ .

Suy ra C < 1 (1)

Lại có 2 020 > 2 019 và 2 022 > 2 021.

Nên 2 020 + 2 022 > 2 019 + 2 021

Suy ra $\frac{2 020 + 2 022}{2 019 + 2 021} > 1$

Mà $\frac{3}{2} > 1$ .

Do đó $\frac{2 020 + 2 022}{2 019 + 2 021} . \frac{3}{2} > 1$ hay D > 1 (2).

Từ (1) và (2) suy ra C < 1 < D.

Vậy C < D.

Bài 127 trang 60,61 sách bài tập Toán lớp 6 Tập 2: Bốn bạn An, Bình, Chi, Đông cùng đọc 4 quyển truyện giống nhau và thi xem ai đọc nhanh hơn. Trong một giờ, các bạn An, Bình, Chi, Đông lần lượt đọc được $\frac{7}{18}; \frac{1}{3}; \frac{23}{60}; \frac{3}{10}$ quyển truyện. Trong bốn bạn đó ai đọc xong nhanh nhất? Ai đọc xong cuối cùng? Giải thích vì sao.

Lời giải:

Ta có: $\frac{7}{18} = \frac{70}{180}$ ; $\frac{1}{3} = \frac{60}{180}$ ; $\frac{23}{60} = \frac{69}{180}$ và $\frac{3}{10} = \frac{54}{180}$ .

Vì 54 < 60 < 69 < 70 nên $\frac{54}{180} < \frac{60}{180} < \frac{69}{180} < \frac{70}{180}$ .

Do đó $\frac{3}{10} < \frac{1}{3} < \frac{23}{60} < \frac{7}{18}$ .

Vậy An đọc xong nhanh nhất, Đông đọc xong cuối cùng.

Bài 128 trang 61 sách bài tập Toán lớp 6 Tập 2: Trong đợt tổng kết năm học tại một trường trung học cơ sở, tổng số học sinh giỏi của ba lớp 6A, 6B, 6C là 90 em. Biết rằng $\frac{2}{5}$ số học sinh giỏi của lớp 6A bằng $\frac{1}{3}$ số học sinh giỏi của lớp 6B và bằng $\frac{1}{2}$ số học sinh giỏi của lớp 6C. Tính số học sinh giỏi của mỗi lớp.

Lời giải:

Số học sinh giỏi của lớp 6A bằng: $\frac{1}{3} : \frac{2}{5} = \frac{5}{6}$ (số học sinh giỏi của lớp 6B).

Số học sinh giỏi của lớp 6C bằng: $\frac{1}{3} : \frac{1}{2} = \frac{2}{3}$ (số học sinh giỏi của lớp 6B).

Tổng số học sinh giỏi của cả ba lớp bằng: $\frac{5}{6} + 1 + \frac{2}{3} = \frac{5}{2}$ (số học sinh giỏi của lớp 6B).

Số học sinh giỏi của lớp 6B là: $90 : \frac{5}{2} = 36$ (học sinh).

Số học sinh giỏi của lớp 6A là: $\frac{5}{6} .36 = 30$ (học sinh).

Số học sinh giỏi của lớp 6C là: 90 – (36 + 30) = 24 (học sinh).

Vậy số học sinh giỏi của lớp 6A, 6B, 6C lần lượt là 36 học sinh, 30 học sinh, 24 học sinh.

Bài 129 trang 61 sách bài tập Toán lớp 6 Tập 2:Cùng một công việc, nếu mỗi đội làm riêng thì ba đội A, B, C hoàn thành công việc trong thời gian lần lượt là 6 giờ, 8 giờ và 12 giờ. Hai đội B và C làm chung trong 2 giờ rồi sau đó đội C chuyển đi làm việc khác, đội A cùng làm với đội B tiếp tục công việc cho đến khi hoàn thành. Đội A cùng làm với đội B cho đến khi hoàn thành công việc trong mấy giờ?

Lời giải:

Trong 1 giờ, đội A, B, C làm được số phần công việc lần lượt là: $\frac{1}{6}; \frac{1}{8}$ và $\frac{1}{12}$ .

Trong 2 giờ, đội B, C làm được số phần công việc lần lượt là: $2. \frac{1}{8} = \frac{1}{4}$ và $2. \frac{1}{12} = \frac{1}{6}$ .

Trong 2 giờ, hai đội B và C làm được $\frac{1}{4} + \frac{1}{6} = \frac{5}{12}$ (công việc).

Số phần công việc còn lại sau khi hai đội B và C làm chung trong 2 giờ là:

$1 - \frac{5}{12} = \frac{7}{12}$ (công việc).

Số phần công việc hai đội A và B làm chung trong 1 giờ là: $\frac{1}{6} + \frac{1}{8} = \frac{7}{24}$ (công việc).

Vậy số giờ để đội A cùng làm với đội B cho đến khi hoàn thành công việc là:

$\frac{7}{12} : \frac{7}{24} = 2$ (giờ).

Bài 130 trang 61 sách bài tập Toán lớp 6 Tập 2: Một người trưởng thành đi 1 dặm (1 mile) khoảng 2 000 bước chân. Các chuyên gia cho rằng nếu người trưởng thành đi bộ đều đặn mỗi ngày khoảng 7 000 bước sẽ giúp cho cơ thể dẻo dai, giảm nguy cơ tim mạch, thoái hóa xương khớp,… 7 000 bước chân (của người trưởng thành) tương ứng với bao nhiêu ki-lô-mét? (Làm tròn kết quả đến hàng phần mười). Biết rằng 1 dặm chuẩn quốc tế ngày nay đã được thống nhất và quy định bằng 1 609,344 m.

Lời giải:

7 000 bước chân (của người trưởng thành) tương ứng với số dặm là:

7 000 : 2 000 = 3,5 (dặm).

Đổi đơn vị: 3,5 dặm = 3,5.1 609,344 m

= 5632,704 m

= 5,632 704 km ≈ 5,6 km.

Vậy 7 000 bước chân (của người trưởng thành) tương ứng với khoảng 5,6 km.

Bài 131 trang 61 sách bài tập Toán lớp 6 Tập 2: Một người trưởng thành trung bình mỗi phút thở 15 lần, mỗi lần hít thở 0,55 lít không khí (Nguồn: optimalbreathing.com). Tính khối lượng không khí một người trưởng thành hít thở trong một ngày (tính theo gam), biết 1 lít không khí nặng 1,3 gam.

Lời giải:

Đổi 1 ngày = 24 giờ = 24 . 60 phút = 1 440 phút.

Số lần hít thở của một người trưởng thành trong một ngày là:

15.1 440 = 21 600 (lần).

Một người trưởng thành hít thở trong một ngày được số lít không khí là:

21 600.0,55 = 11 880 (lít).

Khối lượng không khí một người trưởng thành hít thở trong một ngày là:

11 880.1,3 = 15 444 (g).

Vậy khối lượng không khí một người trưởng thành hít thở trong một ngày là 15 444 g.

Bài 132 trang 61 sách bài tập Toán lớp 6 Tập 2: Các nhà sản xuất cho biết: khi để một chiếc ti vi ở trạng thái “chờ” (nghĩa là chỉ tắt ti vi bằng điều khiển không dây) thì trong một giờ ti vi vẫn tiêu thụ điện năng là 1 Wh (Nguồn: thegreenage.co.uk). Giả thiết trung bình mỗi hộ gia đình ở thành phố Hà Nội đều có một ti vi và xem 4 giờ mỗi ngày. Hãy tính nếu tất cả 1,8 triệu hộ gia đình ở Hà Nội đều tắt ti vi ở trạng thái “chờ” thì trong một tháng (30 ngày) cả thành phố đã để lãng phí bao nhiêu tiền điện? Biết rằng giá điện trung bình là 1 900 đồng/kWh và 1 kWh = 1 000 Wh.

Lời giải:

Trong 1 ngày, mỗi hộ gia đình sẽ để ti vi ở trạng thái “chờ” trong số giờ là:

24 – 4 = 20 (giờ).

Trong 1 tháng, mỗi hộ gia đình sẽ để ti vi ở trạng thái “chờ” trong số giờ là:

20 . 30 = 600 (giờ).

Trong 1 tháng, 1,8 triệu hộ gia đình sẽ để ti vi ở trạng thái “chờ” trong số giờ là:

1 800 000 . 600 = 1 080 000 000 (giờ).

Khi đó trong 1 tháng, 1,8 triệu hộ gia đình để ti vi ở trạng thái “chờ” sẽ tiêu thụ 1 080 000 000 Wh điện.

Đổi đơn vị: 1 kWh = 1 000 Wh.

1 080 000 000 Wh = 1 080 000 kWh.

Số tiền cả thành phố đã lãng phí là:

1 080 000.1 900 = 2 052 000 000 (đồng)

Vậy số tiền cả thành phố đã lãng phí là 2 052 000 000 đồng.

Bài 133 trang 61 sách bài tập Toán lớp 6 Tập 2: Hai xe ô tô chở tất cả 948,6 kg hàng hóa. Nếu chuyển 50% số hàng ở xe thứ nhất sang xe thứ hai thì xe thứ hai chở gấp 3 lần xe thứ nhất. Mỗi xe chở bao nhiêu ki-lô-gam hàng hóa?

Lời giải:

Khi chuyển 50% số hàng ở xe thứ nhất sang xe thứ hai thì xe thứ hai chở gấp 3 lần xe thứ nhất, khi đó xe thứ nhất còn chở số hàng hóa là:

[948,6 : (3 + 1)].1 = 237,15 (kg).

Thực tế xe thứ nhất phải chở: 237,15 : 50% = 474,3 (kg).

Xe thứ hai phải chở: 948,6 – 474,3 = 474,3 (kg).

Vậy mỗi xe đều chở 474,3 kg.

Bài 134 trang 62 sách bài tập Toán lớp 6 Tập 2: Để cấm các loại xe (cơ giới và thô sơ) đi vào đường theo chiều đặt biển, trừ các xe được ưu tiên theo quy định, người ta đặt biển cấm đi ngược chiều. Người đi bộ được phép đi trên vỉa hè hoặc lề đường. Biển báo có dạng hình tròn đường kính 70 cm.

a) Tính diện tích biển báo.

b) Ở chính giữa biển báo là hình chữ nhật được sơn màu trắng có chiều rộng 10 cm, chiều dài 50 cm. Phần còn lại của biển báo được sơn màu đỏ. Tính diện tích phần được sơn màu đỏ của biển báo. (Lấy π = 3,14).

Lời giải:

a) Bán kính của biển báo là: 70 : 2 = 35 (cm).

Diện tích của biển báo là: 35.35.3,14 = 3 846,5 (cm²).

Vậy diện tích của biển báo là 3 846,5 cm².

b) Diện tích của hình chữ nhật được sơn màu trắng là:

10.50 = 500 (cm²).

Vậy diện tích phần được sơn màu đỏ của biển báo là: 3 846,5 – 500 = 3 346,5 cm².

Bài 135 trang 62 sách bài tập Toán lớp 6 Tập 2: Ước lượng kết quả của các tích sau (theo mẫu):

Mẫu: 97,21.5,97 ≈ 97.6 = 582;

121.79 ≈ 120.80 = 9 600.

a) 2 395,11.155,99;

b) (–875,41).(–23,92);

c) (–56 999).1 992.

Lời giải:

a) 2 395,11.155,99 ≈ 2 395.156 = 373 620.

b) (–875,41).(–23,92) = 875,41.23,92 ≈ 875.24 = 21 000.

c) (–56 999).1 992 ≈ (–57 000).1 990 = –113 430 000.

Bài 136 trang 62 sách bài tập Toán lớp 6 Tập 2: Nhân dịp ngày Phụ nữ Việt Nam 20–10, Tâm giúp mẹ bán hoa trong ba ngày. Ngày thứ hai số hoa bán được tăng 10% so với ngày thứ nhất. Ngày thứ ba số hoa bán được giảm 10% so với ngày thứ hai. Trong ngày thứ nhất và ngày thứ ba thì ngày nào Tâm bán được nhiều hoa hơn và nhiều hơn bao nhiêu phần trăm?

Lời giải:

Giả sử số hoa bán được trong ngày thứ nhất là 100% thì số hoa bán được trong ngày thứ hai là: 100% + 10% = 110% (số hoa bán được trong ngày thứ nhất).

Giả sử số hoa bán được trong ngày thứ hai là 100% thì số hoa bán được trong ngày thứ ba là: 100% – 10% = 90% (số hoa bán được trong ngày thứ hai).

So với ngày thứ nhất thì số hoa bán được trong ngày thứ ba là:

110%.90% = 99% (số hoa bán được trong ngày thứ nhất).

Vậy ngày thứ nhất Tâm bán được nhiều hoa hơn ngày thứ ba và nhiều hơn100% – 99% = 1%.

Bài 137 trang 62 sách bài tập Toán lớp 6 Tập 2: Nhân dịp năm mới, một cửa hàng điện máy thực hiện chương trình giảm giá 20% cho tất cả các mặt hàng và ai có thẻ “khách hàng thân thiết” sẽ được giảm tiếp 5% trên giá đã giảm.

a) Bác Nam có thẻ “khách hàng thân thiết” mua một ti vi trị giá 7 900 000 đồng thì phải trả bao nhiêu tiền?

b) Bác Nam mua thêm một ấm đun nước nên phải trả tất cả 6 156 000 đồng. Giá ban đầu của chiếc ấm là bao nhiêu?

Lời giải:

a) Cửa hàng thực hiện chương trình giảm giá 20% nên giá của một chiếc ti vi lúc này bằng 100% – 20% = 80% giá ban đầu.

Số tiền bác Nam phải trả sau khi được giảm 20% là:

7 900 000. 80% = 6 320 000 (đồng).

Do bác Nam có thẻ “khách hàng thân thiết” nên được giảm thêm 5% trên giá đã giảm, nên giá của chiếc ti vi lúc này bằng 100% – 5% = 95% giá đã giảm.

Số tiền bác Nam phải trả sau khi được giảm thêm 5% trên giá đã giảm là:

6 320 000 . 95% = 6 004 000 (đồng).

Vậy số tiền bác Nam phải trả là 6 004 000 đồng.

b) Số tiền bác Nam phải trả khi mua thêm chiếc ấm là:

6 156 000 – 6 004 000 = 152 000 (đồng).

Số tiền bác Nam phải trả cho chiếc ấm trước khi được giảm thêm 5% trên giá đã giảm là: 152 000 : 95% = 160 000 (đồng).

Giá tiền ban đầu của chiếc ấm là: 160 000 : 80% = 200 000 (đồng).

Vậy giá tiền ban đầu của chiếc ấm là 200 000 đồng.

Bài 138 trang 62 sách bài tập Toán lớp 6 Tập 2: Biểu đồ sau đây nói về độ lớn của một số âm thanh trong cuộc sống:

Đơn vị được dùng để đo cường độ âm thanh là decibel (dB). Các âm thanh từ 85dB trở lên (gọi là tiếng ồn) mà tai chúng ta phải tiếp xúc kéo dài hoặc lặp lại nhiều lần có thể làm giảm khả năng nghe hoặc gây điếc.

a) Tỉ lệ độ lớn âm thanh lúc trò chuyện so với độ lớn âm thanh búa khoan là bao nhiêu phần trăm?

b) Dựa vào biểu đồ trên, em hãy nêu ra những tiếng ồn chúng ta nên tránh hoặc hạn chế tiếp xúc.

Lời giải:

a) Tỉ lệ phần trăm giữa độ lớn âm thanh lúc trò chuyện so với độ lớn âm thanh búa khoan là: $\frac{60}{120} .100 % = 50 %$ .

b) Dựa vào biểu đồ trên, những tiếng ồn chúng ta nên tránh hoặc hạn chế tiếp xúc là những âm thanh có cường độ âm thanh từ 85 dB trở lên.

Tức là các âm thanh từ giao thông, máy sấy tóc, nhạc Rock, máy cưa và búa khoan.