Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ một đường tròn (I) tiếp xúc với đường tròn (O) tại C và tiếp xúc với đường kính AB tại D, đường tròn này cắt CA và CB tại các điểm thứ hai là M và N. Chứng minh rằng:a) Ba điểm M, I, N thẳng hàngb) ID⊥MNc) Đường thẳng CD đi qua điểm cố địnhd) Nêu cách dựng đường tròn (I) nói trên.

Câu hỏi:

Cho đường tròn tâm O đường kính AB và một điểm C chạy trên một nửa đường tròn. Vẽ một đường tròn (I) tiếp xúc với đường tròn (O) tại C và tiếp xúc với đường kính AB tại D, đường tròn này cắt CA và CB tại các điểm thứ hai là M và N. Chứng minh rằng:a) Ba điểm M, I, N thẳng hàngb) $\mathrm{ID}\perp \mathrm{MN}$c) Đường thẳng CD đi qua điểm cố địnhd) Nêu cách dựng đường tròn (I) nói trên.

Trả lời:

=> K là điểm chính giữa của cung.Do đó K cố định. Vậy CD luôn đi qua điểm cố định Kd) Để dựng đường tròn (I), ta thực hiện:- Dựng OK vuông góc với AB, với K thuộc nửa đường tròn không chứa điểm C.- Nối CK cắt AB tại D.- Dựng đường thẳng qua D vuông góc với AB cắt CD tại I.- Dựng đường tròn (I; ID) đây chính là đường tròn cần dựng.

====== **** mời các bạn xem câu tiếp bên dưới **** =====

1. Muốn xác định tâm của một đường tròn mà chỉ dùng ê ke thì phải làm như thế nào?
   
   

   Câu hỏi:
   

   Muốn xác định tâm của một đường tròn mà chỉ dùng ê ke thì phải làm như thế nào?

   Trả lời:

   Để xác định tâm của một đường tròn mà chỉ dùng ê ke, ta thực hiện theo các bước sau:Bước 1: Kẻ đường thẳng cắt đường tròn tại A và B.Bước 2: Qua B, dùng ê ke kẻ đường thẳng vuông góc với AB ở B và cắt đường tròn tại C.Bước 3: Nối C với A.Bước 4: Qua A, dùng ê ke kẻ đường thẳng vuông góc với AB tại A và cắt đường tròn tại D.Bước 5: Nối B với D. Giao điểm của AC và BD là tâm đường tròn.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
2. Dựng một tam giác vuông, biết cạnh huyền dài 4 cm và một cạnh góc vuông dài 2,5 cm.
   
   

   Câu hỏi:
   

   Dựng một tam giác vuông, biết cạnh huyền dài 4 cm và một cạnh góc vuông dài 2,5 cm.

   Trả lời:

   Giả sử dựng được tam giác ABC vuông có cạnh huyền BC = 4 cm, cạnh góc vuông AB = 2,5 cm.Gọi O là trung điểm của BC. Ta có: OB = OC = OA = 2 cm.Vậy tam giác ABC nội tiếp đường tròn đường kính BC có cạnh AB = 2,5 cm.Cách dựng: Ta thực hiện các bước sau:Bước 1: Dựng đường tròn bán kính r = 2 cm.Bước 2: Qua O kẻ đường thẳng d cắt đường tròn tại hai điểm B cà CBước 3: Dựng đường tròn tâm B, bán kính 2,5 cm và cắt đường tròn (O) tại ${\mathrm{A}}_1, {\mathrm{A}}_2$.Vậy ${\text{∆A}}_{\text{1}}{\text{BC, ∆A}}_{\text{2}}\text{BC}$ thỏa mãn đề bài.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
3. Cho tam giác ABC. Đường tròn (I) nội tiếp tam giác tiếp xúc với BC, AC, BA theo thứ tự tại D, E, F. Cho biết BAC^=EDF^. Tính số đo của góc BAC^.
   
   

   Câu hỏi:
   

   Cho tam giác ABC. Đường tròn (I) nội tiếp tam giác tiếp xúc với BC, AC, BA theo thứ tự tại D, E, F. Cho biết $\widehat{\mathrm{BAC}}=\widehat{\mathrm{EDF}}$. Tính số đo của góc $\widehat{\mathrm{BAC}}$.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
4. Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.
   
   

   Câu hỏi:
   

   Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.

   Trả lời:

   Ta có $\widehat{\mathrm{AMB}}, \widehat{\mathrm{ANB}}$ là các góc nội tiếp chắn nửa đường tròn nên: $\widehat{\mathrm{AMB}}=\widehat{\mathrm{ANB}}={90}^0$Do đó, $\mathrm{BM}\perp \text{AS,\hspace{0.17em}\hspace{0.17em}AN}\perp \text{SB}$$\Rightarrow \mathrm{H}$ là trực tâm của tam giác SAB.Vậy ta được $\mathrm{AH}\perp \mathrm{AB}$.

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====
   
5. Cho đường tròn (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D. Gọi K là giao điểm của EB với đường tròn (O) và H là giao điểm của BD và AK.a) ∆ABE là tam giác gì?b) Chứng minh rằng EH vuông góc với AB.c) Chứng minh rằng OD vuông góc với AK.
   
   

   Câu hỏi:
   

   Cho đường tròn (O), đường kính AB, điểm D thuộc đường tròn. Gọi E là điểm đối xứng với A qua D. Gọi K là giao điểm của EB với đường tròn (O) và H là giao điểm của BD và AK.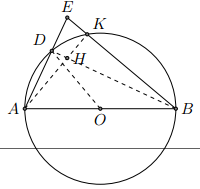a) $∆$ABE là tam giác gì?b) Chứng minh rằng EH vuông góc với AB.c) Chứng minh rằng OD vuông góc với AK.

   Trả lời:

   

   ====== **** mời các bạn xem câu tiếp bên dưới **** =====