Đề thi Giữa học kì 1 Toán lớp 8 Hà Nội năm 2022 (6 đề) – Đề 1
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1 Hà Nội
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 1)
PHẦN I. TRẮC NGHIỆM (1 điểm). Viết lại chữ cái đứng trước đáp án đúng trong các câu sau vào bài kiểm tra.
Câu 1. Kết quả rút gọn biểu thức: (3x + 2)(3x – 2) là:
A) 3x2 + 4 B) 3x2 – 4 C) 9x2 + 4 D) 9x2 -4
Câu 2. Đơn thức 12x2y3z chia hết cho đơn thức nào sau đây?
A) 3x3yz B) 4xy2z2 C) -5xy2 D) 3xyz2
Câu 3. Khẳng định nào sau đây là đúng?
A. Tứ giác có hai đường chéo bằng nhau là hình chữ nhật.
B. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật
C. Hình thang có một góc vuông là hình chữ nhật
D. Hình thang cân có hai đường chéo bằng nhau là hình chữ nhật.
Câu 4. Hình nào dưới đây luôn có tâm đối xứng?
A. Hình thang B. Hình thang cân C. Hình bình hành D. Cả A, B, C
PHẦN II. TỰ LUẬN (9 điểm).
Bài 1 (2 điểm). Phân tích các đa thức sau thành nhân tử.
a) 2xy + 3z + 6y +xz
b) 16x2 -(x +1)2
c) x2 – 6x -7
d) x3 – 2x2 + 2x -1
Bài 2 (1,5 điểm) Tìm x, biết:
a) x(x – 2) – x + 2= 0
b) x2 – 25 – (x + 5) = 0
c) (10x + 9)x – (5x – 1)(2x + 3)=0
Bài 3 (1 điểm).
a) Rút gọn rồi tính giá trị của biểu thức sau:
(x – y)(x2 + xy + y2 ) + 2y3 tại 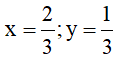
b) Làm tính chia: ( 30x4y3 – 20x2y3 + 6x4y4) : 5x2y3
Bài 4 (3,5 điểm). Cho hình bình hành ABCD, các đường chéo cắt nhau tại O. Gọi E, F theo thứ tự là trung điểm của OB, OD.
a) Tứ giác AECF là hình gì? Vì sao?
b) Gọi H là giao điểm của AF và DC, K là giao điểm của CE và AB. Chứng minh AH = CK
c) Qua O kẻ đường thẳng song song với CK cắt DC tại I.
Chứng minh rằng: DI = 2CI
Bài 5 (1 điểm). Ông Văn có 24m hàng rào rất đẹp, ông muốn rào một sân vườn hình chữ nhật để đạt được diện tích lớn nhất. Vườn ngay sát tường nhà để một chiều không phải rào. Hỏi kích thước sân vườn đó là bao nhiêu?

………………………………………………………………………….
Đề thi Giữa học kì 1 Toán lớp 8 Hà Nội năm 2022 (6 đề) – Đề 2
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1 Hà Nội
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 2)
I. TRẮC NGHIỆM (1,5 điểm) Ghi lại chữ cái đứng trước câu trả lời đúng
Câu 1. Đơn thức thích hợp điền vào chỗ trống của 9x2 +….+ 25 =(3x + 5)2 là
A. 30x B. -20x C. 10x D. 25x
Câu 2. Kết quả phân tích đa thức x2 -2x – y2 + 1 thành nhân tử là:
A. (x – 1 + y)(x + 1 + y)
B. (x – 1 – y)(x + 1 + y)
C. (x – 1 – y)(x – 1 + y)
D. (x + 1 – y)(x -1 + y)
Câu 3. Giá trị của x để x2 = 3x là:
A. B.{ 0; -3} C. {±3} D.
Câu 4. Số trục đối xứng của tam giác đều là:
A. 1 B.2
C.3 D.4
Câu 5. Hình thang ABCD AB // CD , M là trung điểm AD, N là trung điểm BC. Biết:
CD = 8cm, MN = 6cm. Độ dài đoạn AB là:
A. 2cm B. 4cm
C. 6cm D. 8cm
Câu 6. Tứ giác ABCD là hình bình hành nếu có:
A.  B. AB // CD
B. AB // CD
C. AB = CD; BC = AD D. BC = DA
II. TỰ LUẬN (8,5 điểm)
Bài 1. (1,5 điểm) Cho biểu thức sau:
A= (x – 1)( x + 1) + (x – 2)(x2 + 2x + 4) – x(x2 + x -2)
a) Rút gọn biểu thức A.
b) Tính giá trị của biểu thức A tại 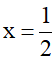 .
.
Bài 2. (1,5 điểm) Phân tích các đa thức sau thành nhân tử:
a) 3x3 – 6x2y + 3xy2
b) x3 – 3x2 – 4x + 12
c) (x2 + x)2 – 4(x2 + x) -12
Bài 3 (1,5 điểm): Tìm x biết:
a) (3x + 5)(2x – 1) -6x(x + 2) = x
b) x3 – 5x2 -14x = 0
c) 2(x + 3) – x2 -3x = 0
Bài 4 (3,5 điểm): Cho hình thang vuông ABCD  có
có 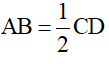 . Kẻ
. Kẻ  tại H. Gọi M là trung điểm của đoạn CH, N là trung điểm của đoạn DH.
tại H. Gọi M là trung điểm của đoạn CH, N là trung điểm của đoạn DH.
a) Chứng minh: Tứ giác ABMN là hình bình hành.
b) Gọi I là trung điểm của CD. Chứng minh H và C đối xứng nhau qua MI.
c) Chứng minh: N là trực tâm của tam giác ADM.
d) Chứng minh: AB2 + AD2 = MB2 + MD2
Bài 5. (0,5 điểm)
Cho a, b là các số dương thỏa mãn a9 + b9 = a10 + b10= a11 + b11.
Tính giá trị của biểu thức P= a2018 + b2018 + 2018 .
………………………………………………………………………….
Đề thi Giữa học kì 1 Toán lớp 8 Hà Nội năm 2022 (6 đề) – Đề 3
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1 Hà Nội
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 3)
Bài 1: (2 điểm) Phân tích đa thức thành nhân tử
a) xy + xz + 3y + 3z
b) x2 + 2x – 3
Bài 2: (2 điểm) Cho A = [(3x – 2)(x + 1) – (2x + 5)(x2 – 1)]:(x + 1)
Tính giá trị của A khi x= 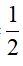 .
.
Bài 3: (2 điểm) Tìm x biết:
a) 6x2 – (2x – 3)(3x + 2) = 1
b) (x + 1)3 – (x – 1)(x2 + x + 1) – 2 = 0
Bài 4: (3,5 điểm)
Cho tam giác ABC vuông tại A, lấy điểm M thuộc cạnh huyền BC (M không trung B và C). Gọi D và E theo thứ tự là chân đường vuông góc kẻ từ M đến AB, AC
a) Tứ giác AEMD là hình gì?
b) Gọi P là điểm đối xứng của M qua D, K là điểm đối xứng của của M qua E và I là trung điểm của DE. Chứng minh P đối xứng với K qua A
c) Khi M chuyển động trên đoạn BC thì I chuyển động trên đường nào?
Bài 5: (0,5 điểm): Cho x, y Z chứng minh rằng:
N = (x – y)(x – 2y)(x – 3y)(x – 4y) + y4 là số chính phương.
————-HẾT———–

Đề thi Giữa học kì 1 Toán lớp 8 Hà Nội năm 2022 (6 đề) – Đề 4
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1 Hà Nội
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 4)
Bài 1. (2 điểm) Rút gọn các biểu thức:
a) (x + 2)2 – (x + 3)(x – 3) + 10
b) (x + 5)( x2 – 5x + 25)- x(x – 4)2 + 16x
c) (x-2y)3 – (x + 2y)( x2 -2xy + 4y2) + 6x2y
Bài 2. (2,0 điểm) Phân tích đa thức thành nhân tử:
a) 8x2y – 8xy + 2x
b) x2 – 6x – y2 + 9
c) (x2 + 2x)(x2 + 4x + 3) – 24
Bài 3. (2 điểm) Tìm x, biết:
a) (x + 3)2 – (x +2)(x – 2)= 4x +17
b) (x-3)(x2 + 3x +9) – x(x2-4) = 1
c) 3x2 + 7x =10
Bài 4. (3 điểm) Cho hình bình hành ABCD. Trên đường chéo BD lấy 2 điểm M và N sao cho BM= DN=  BD
BD
a) Chứng minh rằng: ΔAMB = ΔCND
b) AC cắt BD tại O. Chứng minh tứ giác AMCN là hình bình hành.
c) AM cắt BC tại I. Chứng minh: AM = 2MI
d) CN cắt AD tại K. Chứng minh: I và K đối xứng với nhau qua O
Bài 5 (1 điểm)
a) Tìm GTLN của biểu thức: A = 5 + 2xy + 14y -x2 -5y2 -2x
b) Tìm tất cả số nguyên dương n sao cho B= 2n + 3n + 4n là số chính phương.
(Giám thị coi thi không giải thích gì thêm)
………………………………………………………………………….
Đề thi Giữa học kì 1 Toán lớp 8 Hà Nội năm 2022 (6 đề) – Đề 5
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1 Hà Nội
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 5)
Bài 1 (4,5 điểm). Phân tích các đa thức sau thành nhân tử:
a) 4x2 + 4x3 -x2 -x
b) 1 – 2a + 2bc + a2 -b2 – c2
c) ( x – 7)( x – 5)(x – 4)(x – 2) – 72
Bài 2 (1,5 điểm). Tìm x sao cho:
(x + 5)(4 – 3x)- (3x+ 2)2 + (2x + 1)3 = (2x – 1)(4x2 + 2x + 1)
Bài 3 (3 điểm). Cho có M và N lần lượt là trung điểm của các cạnh BC và AC. Trên tia đối của tia MN lấy điểm D sao cho NM = ND. Gọi I là trung điểm của đoạn thẳng AM.
a) Tứ giác ADCM là hình gì? vì sao?
b) Chứng minh rằng: B, I, D thẳng hàng.
c) Qua điểm D kẻ đường thẳng song song với AC, cắt đường thẳng BC tại E. Đường thẳng IN cắt DE tại F. Tìm điều kiện của để tứ giác MNFE là hình thang cân.
Bài 4 (1 điểm).
a) Tìm giá trị nhỏ nhất của biểu thức A = 2x2 – x + 2017
b) (Dành riêng cho lớp 8A)
Cho ba số nguyên a, b, c có tổng chia hết cho 6
Chứng minh rằng biểu thức M= (a+b)(b+c)(c+a) – 2abc chia hết cho 6
………………………………………………………………………….
Đề thi Giữa học kì 1 Toán lớp 8 Hà Nội năm 2022 (6 đề) – Đề 6
Phòng Giáo dục và Đào tạo …..
Đề thi Giữa Học kì 1 Hà Nội
Năm học 2022 – 2023
Bài thi môn: Toán lớp 8
Thời gian làm bài: 60 phút
(không kể thời gian phát đề)
(Đề số 6)
Bài 1: (2,0 điểm) Thực hiện phép tính:
a) 2x2(3x2 – 7x -3)
b) (16x4 – 20x2y3 – 4x5y) : (-4x2 )
Bài 2: (2,0 điểm) Phân tích đa thức thành nhân tử:
a) x2 – 3x +xy -3y
b) 16(2x + 3)2 – 9(5x-2)2
Bài 3: (2,0 điểm) Tìm biết:
a) 2018x – 1 + 2019x(1 – 2018x) = 0
b) (x + 2)3 – x2(x – 6) – 4
Bài 4: (3,5 điểm) Cho vuông tại A (AB < AC), trung tuyến AM. Kẻ MN ⊥ AB, MP ⊥ AC (N ∈ AB, P ∈ AC)
a) Chứng minh: AC = 2MN
b) Chứng minh tứ giác BMPN là hình gì? Tại sao?
c) Gọi E là trung điểm của BM, F là giao điểm của AM và PN. Chứng minh tứ giác ABEF là hình thang cân
d) Kẻ AH ⊥ BC, MK // AH (H ∈ BC, K ∈ AC). Chứng minh BK ⊥ HN
Bài 5: (0,5 điểm) Cho các số a, b dương thỏa mãn: a3 + b3 = 3ab -1
Chứng minh rằng: a2018 + b2018 =2