Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Chương 1 : Sơ lược về khái niệm và lịch sử
Chương 2 : Các biến đổi lượng giác
Chương 3: Hệ thức lượng trong tam giác
Biến đổi lượng giác và hệ thức lượng
Chương 1 : Sơ lược về khái niệm và lịch sử
I. Khái niệm
Trong toán học nói chung và lượng giác học nói riêng, các hàm lượng giác là các hàm toán học của góc, được dùng khi nghiên cứu tam giác và các hiện tượng có tính chất tuần hoàn. Các hàm lượng giác của một góc thường được định nghĩa bởi tỷ lệ chiều dài hai cạnh của tam giác vuông chứa góc đó, hoặc tỷ lệ chiều dài giữa các đoạn thẳng nối các điểm đặc biệt trên vòng tròn đơn vị. Sâu xa hơn, ở khía cạnh hiện đại hơn, định nghĩa hàm lượng giác là chuỗi vô hạn hoặc là nghiệm của phương trình vi phân, điều này cho phép hàm lượng giác có thể có đối số là một số thực hay một số phức bất kỳ.
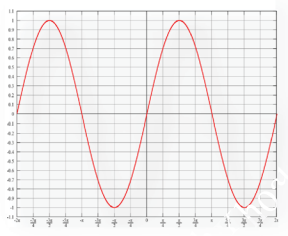
( Dạng đồ thị hàm sin )
II. Lịch sử
Những nghiên cứu một cách hệ thống và việc lập bảng tính các hàm lượng giác được cho là thực hiện đầu tiên bởi Hipparchus \(^{(1)}(180 – 125{\rm{TCN}})\), người đã lập bảng tính độ dài các cung tròn và chiều dài của dây cung tương ứng. Sau đó, Ptomely \(^{(2)}\) tiếp tục phát triển công trình, tìm ra công thức cộng và trừ cho \(\sin (A + B)\) và \(\cos (A + B)\), Ptomely cũng đã suy diễn ra được công thức hạ bậc, cho phép ông lập bảng tính với bất kỳ độ chính xác cần thiết nào. Tuy nhiên, những bảng tính trên đều đã bị thất truyền. Các phát triển tiếp theo diễn ra ở Ấn Độ, công trình của Surya Siddhanta \(^{(3)}\) (thế kỷ 4-5) định nghĩa hàm sin theo nửa góc và nửa dây cung. Đến thế kỷ 10 , người Ả Rập đã dùng cả 6 hàm lượng giác cơ bản với độ chính xác đến 8 chữ số thập phân.
Các công trình đầu tiên này về các hàm lượng giác cơ bản đều được phát triển nhằm phục vụ trong các công trình thiên văn học, cụ thể là dùng để tính toán các đồng hồ mặt trời.
Ngày nay, chúng được dùng để đo khoảng cách tới các ngôi sao gần, giữa các mốc giới hạn hay trong các hệ thống hoa tiêu vệ tinh. Rộng hơn nữa, chúng được áp dụng vào nhiều lĩnh vực khác : quang học, phân tích thị trường tài chính, điện tử học, lý thuyết xác suất, thống kê, sinh học, dược khoa, hóa học, lý thuyết số, địa chấn học, khí tượng học, hải dương học…
Ta lấy ví dụ từ một bài toán sau trích từ Lucia C. Hamson, Daylight, Twilight, Darkness and Time:
Việc mô hình hóa về số giờ chiếu sáng của mặt trời là hàm thời gian trong năm tại nhiều vĩ độ khác nhau. Cho biết Philadelphia nằm ở vĩ độ Bắc, tìm hàm biều thị số giờ chiếu sáng của mặt trời tại Philadelphia.

Chú ý rằng mỗi đường cong tương tự với một hàm số sin mà bị di chuyển và kéo căng ra. Tại độ cao của Philadelphia, thời gian chiếu sáng kéo dài 14,8 giờ vào ngày 21 tháng 6 và 9,2 giờ vào ngày 21 tháng 12 , vậy nên biên độ của đường cong (hệ số kéo căng theo chiều dọc) là : \(\frac{1}{2}(14,8 – 9,2) = 2,8\)
Hệ số nào mà chúng ta cần để kéo căng đồ thị hình sin theo chiều ngang nếu chúng ta đo thời gian t trong ngày? Bởi có 365 ngày/ năm, chu kỳ của mô hình nên là 365 . Nhưng mà giai đoạn của \(y = \sin t\) là \(2\pi \), nên hệ số kéo căng theo chiều ngang là :
\(c = \frac{{2\pi }}{{365}}\)
Chúng ta cũng để ý rằng đường cong bắt đầu một chu trình của nó vào ngày 21 tháng 3 , ngày thứ 80 của năm nên chúng ta phải phải dịch chuyển đường cong về bên phải 80 đơn vị. Ngoài ra, chúng ta phải đưa nó lên trên 12 đơn vị. Do đó chúng ta mô hình hóa số giờ chiếu sáng của của mặt trời trong năm ở Philadelphia vào ngày thứ t của năm bằng hàm số :
\(L(t) = 12 + 2,8\sin \left[ {\frac{{2\pi }}{{365}}(t – 80)} \right]\)
Chương 2 : Các biến đổi lượng giác
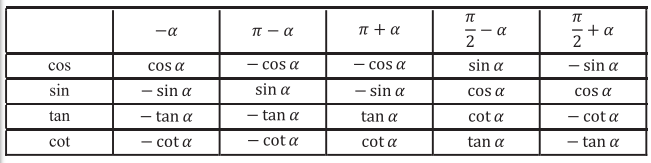
I. Bảng giá trị lượng giác của các cung có liên quan đặc biệt
Ta gọi cung có liên quan đặc biệt với cung \(\alpha \) là các cung :
– Đối với \(\alpha : – \alpha \)
– Bù với \(\alpha :\pi – \alpha \)
Hiệu \(\pi \) với \(\alpha :\pi + \alpha \)
Hơn kém \(\frac{\pi }{2}\) với \(\alpha :\frac{\pi }{2} \pm \alpha \)
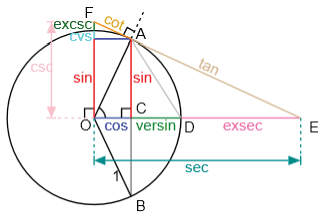
Ngoài ra, có một số hàm lượng giác khác :
\( – \sec \alpha = \frac{1}{{\cos \alpha }}\quad – \csc \alpha = \frac{1}{{\sin \alpha }}\)
\( – {\mathop{\rm versin}\nolimits} \alpha = 1 – \cos \alpha \quad – {\mathop{\rm exsec}\nolimits} \alpha = \sec \alpha – 1\)
II. Công thức lượng giác
1. Công thức cơ bản
\(\begin{array}{l}{\sin ^2}x + {\cos ^2}x = 1\quad \\\tan x\cot x = 1\left( {x \ne k\frac{\pi }{2},k \in \mathbb{Z}} \right)\end{array}\)
\[1 + {\tan ^2}x = \frac{1}{{{{\cos }^2}x}}\left( {x \ne \frac{\pi }{2} + k\pi ,k} \right. \in \mathbb{Z})\]
\[\begin{array}{*{20}{l}}{\tan x = \frac{{\sin x}}{{\cos x}}}&{}\\{\cot x = \frac{{\cos x}}{{\sin x}}}&{}\end{array}\]
\[1 + {\cot ^2}x = \frac{1}{{{{\sin }^2}x}}(x \ne k\pi ,k \in \mathbb{Z})\]
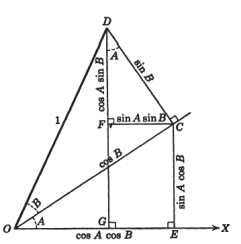
Từ hình vẽ thực tiễn trên, ta rút ra được một số công thức cơ bản về hàm lượng giác :
2. Công thức cộng
\(\begin{array}{l}\sin (a \pm b) = \sin a\cos b \pm \sin b\cos a\\\cos (a + b) = \cos a\cos b \mp \sin a\sin b\\\tan (a \pm b) = \frac{{\tan a \pm \tan b}}{{1 \mp \tan a\tan b}}\quad \left( {a,b,a \pm b \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\\\cot (a \pm b) = \frac{{\cot a\cot b \mp 1}}{{\cot a \pm \cot b}}\quad (a,b,a \pm b \ne k\pi ,k \in \mathbb{Z})\end{array}\)
3. Công thức nhân 2
a. Công thức nhân 2
\(\sin 2x = 2\sin x\cos x\)
\[\begin{array}{l}\cos 2x = \left\{ {\begin{array}{*{20}{l}}{{{\cos }^2}x – {{\sin }^2}x}\\{2{{\cos }^2}x – 1}\\{1 – 2{{\sin }^2}x}\end{array}} \right.\\\tan 2x = \frac{{2\tan x}}{{1 – {{\tan }^2}x}}\quad \left( {x,2x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right)\end{array}\]
b. Công thức nhân 3
\(\sin 3x = 3\sin x – 4{\sin ^3}x = 4\sin x\sin \left( {\frac{\pi }{3} – x} \right)\sin \left( {\frac{\pi }{3} + x} \right)\)
\(\begin{array}{l}\cos 3x = 4{\cos ^3}x – 3\cos x = 4\cos x\cos \left( {\frac{\pi }{3} – x} \right)\cos \left( {\frac{\pi }{3} + x} \right)n\\\tan 3x = \frac{{3\tan x – {{\tan }^3}x}}{{1 – 3{{\tan }^2}x}} = \tan x\tan \left( {\frac{\pi }{3} – x} \right)\tan \left( {\frac{\pi }{3} + x} \right)\end{array}\)
Công thức tổng quát đối với hàm \(\tan \) :
\(\tan (a + b + c) = \frac{{\tan a + \tan b + \tan c – \tan a\tan b\tan c}}{{1 – \tan a\tan b – \tan b\tan c – \tan c\tan a}}\)
Xem thêm