Bài tập Toán 8 Chương 1 Bài 11: Chia đa thức cho đơn thức
A. Bài tập Chia đa thức cho đơn thức
I. Bài tập trắc nghiệm
Bài 1: Đa thức M thỏa mãn xy2 + x2y2 + x3y = (5xy).M là ?
A. M = y + xy2 + x2
B. M = y + xy + x2
C. M = – y + x2y + x2
D. Cả A, B, C đều sai.
Lời giải:
Ta có xy2 + x2y2 + x3y = ( 5xy ).M
⇒ M = ( xy2 + x2y2 + x3y ):( 5xy )
= y + xy + x2.
Chọn đáp án B.
Bài 2: Kết quả nào sau đây đúng?
A. ( – 3x3 + 5x2y – 2x2y2 ):( – 2 ) = – x3 – x2y + x2y2
B. ( 3x3 – x2y + 5xy2 ):(x ) = 6x2 – 2xy + 10y2
C. ( 2x4 – x3 + 3x2 ):( –x ) = 6x2 + 3x – 9
D. ( 15x2 – 12x2y2 + 6xy3 ):( 3xy ) = 5x – 4xy – 2y2
Lời giải:
Ta có:
+ ( – 3x3 + 5x2y – 2x2y2 ):( – 2 ) = x3 – x2y + x2y2
⇒ Đáp án A sai.
+ ( 3x3 – x2y + 5xy2 ):( x ) = 6x2 – 2xy + 10y2
⇒ Đáp án B đúng.
+ ( 2x4 – x3 + 3x2):( – x ) = – 6x3 + 3x2 – 9x
⇒ Đáp án C sai.
+ ( 15x2 – 12x2y2 + 6xy3 ):( 3xy ) = – 4xy – 2y2
⇒ Đáp án D sai.
Chọn đáp án B.
Bài 3: Giá trị của biểu thức A = [ ( x – y )5 + ( x – y )4 + ( x – y )3 ]:( x – y ) với x = 3, y = 1 là ?
A. A = 28
B. A = 16
C. A = 20
D. A = 14
Lời giải:
Ta có A = [ ( x – y )5 + ( x – y )4 + ( x – y )3 ]:( x – y )
= ( x – y )4 + ( x – y )3 + ( x – y )2
Với x = 3, y = 1 ta có A = ( 3 – 1 )4 + ( 3 – 1 )3 + ( 3 – 1 )2
= 24 + 23 + 22 = 16 + 8 + 4 = 28.
Chọn đáp án A.
Bài 4:
Lời giải:
Chọn đáp án A
Bài 5:
Lời giải:
Chọn đáp án C
Bài 6: Cho đa thức
đơn thức B = 2x .Không làm tính chia, hãy xét xem đa thức A có chia hết cho đơn thức B hay không?
A. Không
B. Có
C. Chưa thể kết luận
D. Tất cả sai
Lời giải:
Hạng tử y6 của đa thức A không chia hết cho đơn thức B = 2x.
Do đó, đa thức A không chia hết cho đơn thức B
Chọn đáp án A
Bài 7: Thực hiện phép chia:
Lời giải:
Chọn đáp án A
Bài 8: Tính giá trị biểu thức A tại x = -2; y = 102; z = 102
A. 1029
B. -1028
C. 30
D. -1
Lời giải:
Giá trị biểu thức tại x = -2; y = 102; z= 102 là:
Chọn đáp án D
Bài 9: Thưc hiện phép tính chia:
Lời giải:
Chọn đáp án C
Bài 10: Làm tính chia:
Lời giải:
Chọn đáp án A
Bài 11: Chọn câu đúng nhất
A. Thương của phép chia đa thức cho đơn thức
là
B. Thương của phép chia đa thức cho đơn thức ax2 là
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải:
Ta có
Đáp án cần chọn là: C
Bài 12: Cho A = (3a2b)3(ab3)2; B = (a2b)4. Khi đó A : B bằng
A. 27ab5
B. -27b5
C. 27b5
D. 9b5
Lời giải:
Ta có
A = (3a2b)3(ab3)2 = 33.(a2)3.b3.a2(b3)2
= 27a6.b3.a2.b6 = 27a8b9
B = (a2b)4 = (a2)4.b4 = a8b4
Khi đó A : B = 27a8b9 : a8b4 = 27b5
Đáp án cần chọn là: C
Bài 13: Cho A = (4x2y2)2(xy3)3; B = (x2y3)2. Khi đó A : B bằng
A. 16x4y6
B. 8x3y8
C. 4x3y7
D. 16x3y7
Lời giải:
Ta có A = (4x2y2)2(xy3)3 = 42(x2)2(y2)2x3(y3)3 = 16x4y4x3y9 = 16x7y13
B = (x2y3)2 = (x2)2(y3)2 = x4y6
Khi đó A : B = 16x7y13 : x4y6 = 16x3y7
Đáp án cần chọn là: D
Bài 14: Cho (2x+ y2).(…) = 8x3 + y6. Điền vào chỗ trống (…) đa thức thích hợp
A. 2x2 – 2xy + y4
B. 2x2 – 2xy + y2
C. 4x2 – 2xy2 + y4
D. 4x2 + 2xy + y4
Lời giải:
Ta có
8x3 + y6 = (2x)3 + (y2)3
= (2x + y2)((2x)2 – 2x.y2 + (y2)2)
= (2x + y2)(4x2 – 2xy2 + y4)
Vậy đa thức cần điền là 4x2 – 2xy2 + y4
Đáp án cần chọn là: C
Bài 15: Cho (3x – 4y).(…) = 27x3 – 64y3. Điền vào chỗ trống (…) đa thức thích hợp
A. 6x2 + 12xy + 8y2
B. 9x2 + 12xy + 16y2
C. 9x2 – 12xy + 16y2
D. 3x2 + 12xy + 4y2
Lời giải:
Ta có:
27x3 – 64y3 = (3x)3 – (4y)3 = (3x – 4y)((3x)2 + 3x.4y + (4y)2)
= (3x – 4y)(9x2 + 12xy + 16)
Vậy đa thức cần điền là 9x2 + 12xy + 16
Đáp án cần chọn là: B
Bài 16: Cho (27x3 + 27x2 + 9x + 1) : (3x + 1)2 = (…) Điền vào chỗ trống đa thức thích hợp
A. (3x + 1)5
B. 3x + 1
C. 3x – 1
D. (3x + 1)3
Lời giải
Ta có:
(27x3 + 27x2 + 9x + 1) : (3x + 1)2
= (3x + 1)3 : (3x + 1)2 = 3x + 1
Đáp án cần chọn là: B
II. Bài tập tự luận
Bài 1: Thực hiện phép tính
a, (12x4y3 + 8x3y2 – 4xy2):2xy.
b, (- 2x5 + 6x2 – 4x3):2x2
Lời giải:
a) Ta có: (12x4y3 + 8x3y2 – 4xy2):2xy = (12x4y3:2xy) + (8x3y2:2xy) – (4xy2:2xy)
= 6x4 – 1.y3 – 1 + 4x3 – 1.y2 – 1 – 2x1 – 1.y2 – 1 = 6x3y2 + 4x2y – 2y
b) Ta có: (- 2x5 + 6x2 – 4x3):2x2 = (- 2x5:2x2) + (6x2:2x2) – (4x3:2x2)
= – x5 – 2 + 3x2 – 2 – 2x3 – 2 = – x3 – 2x + 3.
Bài 2: Thực hiện các phép tính sau: (a2x4 + ax3 – ax2):(-ax2)
Lời giải:
Ta có: (a2x4 + ax3 – ax2):(-ax2)
= (a2x4: – ax2) + (ax3: – ax2) + (- ax2: – ax2)
= – ax2 – 2x + 1
Bài 3: Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7xn – 1y5 – 5x3y4;
B = 5x2yn
Lời giải:
Ta có A:B = (7xn – 1 y5 – 5x3y4):(5x2yn) = xn – 3 y5 – n – xy4 – n
Theo đề bài đa thức A chia hết cho đơn thức B
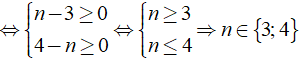
Vậy giá trị n cần tìm là n∈{3; 4}.
Bài 4: Thực hiện các phép tính: 4(x – 1) + (12x2 – 3x):(- 3x) – (2x + 1).
Lời giải:
Ta có 4(x – 1) + (12x2 – 3x):(- 3x ) – (2x + 1)
= 4(x – 1) + [(12x2: – 3x) + (- 3x: – 3x)] – (2x + 1)
= 4(x – 1) + (- 4x + 1) – (2x + 1) = 3x – 4 + 1 – 4x – 2x – 1 = – 3x – 4
Bài 5: Tìm đa thức A biết:
a, A.6x4 = 24x9 – 30x8 +x5
b, A.(- x3y2) = 5x6y4 + x5y3 – 10x3y2
Lời giải:
a) Ta có: A.6x4 = 24x9 – 30x8 +x5 ⇒ A = (24x9 – 30x8 + x5):(6x4)
⇔ A =x9 – 4 – x8 – 4 + x5 – 4 = 4x5 – 5x4 + x
Vậy A = 4x5 – 5x4 + x.
b) Ta có A.(- x3y2) = 5x6y4 + x5y3 – 10x3y2 ⇒ A = (5x6y4 + x5y3 – 10x3y2):(- x3y2)
⇔ A = – 2x6 – 3y4 – 2 – 3x5 – 3y3 – 2 + 4x3 – 3y2 – 2
Vậy A = – 2x3y2 – 3x2y + 1.
Bài 6: Không làm tính chia, hãy xét xem đa thức A có chia hết cho đơn thức B không:
A = 15xy2 + 17xy3 + 18y2
B = 6y2.
Lời giải:
A chia hết cho B vì mỗi hạng tử của A đều chia hết cho B (mỗi hạng tử của A đều có chứa nhân tử y với số mũ lớn hơn hay bằng 2 bằng với số mũ của y trong B).
Bài 7: Làm tính chia:
a) (-2x5 + 3x2 – 4x3) : 2x2;
b) (x3 – 2x2y + 3xy2) : (-x);
Lời giải:
a) (-2x5 + 3x2 – 4x3) : 2x2 = (-)x5 – 2 +x2 – 2 + (-)x3 – 2 = – x3 + – 2x.
b) (x3 – 2x2y + 3xy2) : (-x) = (x3 : – x) + (-2x2y : – ) + (3xy2 : – x) = -2x2+ 4xy – 6y2 = -2x(x + 2y + 3y2).
Bài 8: Làm tính chia: [3(x – y)4 + 2(x – y)3 – 5(x – y)2] : (y – x)2
(Gợi ý, có thế đặt x – y = z rồi áp dụng quy tắc chia đa thức cho đơn thức)
Lời giải:
[3(x – y)4 + 2(x – y)3 – 5(x – y)2] : (y – x)2
= [3(x – y)4 + 2(x – y)3 – 5(x – y)2] : [-(x – y)]2
= [3(x – y)4 + 2(x – y)3 – 5(x – y)2] : (x – y)2
= 3(x – y)4 : (x – y)2 + 2(x – y)3 : (x – y)2 + [– 5(x – y)2 : (x – y)2]
= 3(x – y)2 + 2(x – y) – 5
Bài 9: Thực hiện phép tính:
a, (7.35 – 34 + 36) : 34
b, (163 – 642) : 83
Lời giải:
a, (7.35 – 34 + 36) : 34
= (7.35 : 34) + (– 34 : 34 + (36 : 34)
= 7.3 – 1 + 32
= 21 – 1 + 9 = 29
b, (163 – 642) : 83
= [(2.8)3 – (82)2] : 83
= (23.83 – 84) : 83
= (23.83 : 83) + (- 84 : 83)
= 23 – 8 = 8 – 8 = 0
Bài 10: Làm tính chia: (3x2y2 + 6x2y3 – 12xy) : 3xy.
Lời giải:
(3x2y2 + 6x2y3 – 12xy) : 3xy
= (3x2y2 : 3xy) + (6x2y2 : 3xy) + (-12xy : 3xy)
= xy + 2xy2 – 4.
III. Bài tập vận dụng
Bài 1:
Ai đúng, ai sai?
Khi giải bài tập: “Xét xem đa thức A = 5x4 – 4x3 + 6x2y có chia hết cho đơn thức B = 2x2 hay không”,
Hà trả lời: “A không chia hết cho B vì 5 không chia hết cho 2”,
Quang trả lời: “A chia hết cho B vì mọi hạng tử của A đều chia hết cho B”.
Cho biết ý kiến của em về lời giải của hai bạn.
Bài 2: Làm tính chia:
a, (5x4 – 3x3 + x2) : 3x2
b, (5xy2 + 9xy – x2y2) : (- xy)
c, (x3y3 – x2y3 – x3y2) : x2y2
Bài 3: Tìm n để mỗi phép chia sau là phép chia hết (n là số tự nhiên)
a, (5x3 – 7x2 + x) : 3xn
b, (13x4y3 – 5x3y3 + 6x2y2) : 5xnyn
Bài 4: Làm tính chia:
a, [5(a – b)3 + 2(a – b)2] : (b – a)2
b, 5(x – 2y)3 : (5x – 10y)
c, (x3 + 8y3) : (x + 2y)
Bài 5: Tìm giá trị nguyên của n để giá trị biểu thức 4n3 – 4n2 – n + 4 chia hết cho giá trị của biểu thức 2n + 1.
Bài 6: Tìm m sao cho đa thức A chia hết cho đa thức B biết.
a) A = 8x2 – 26x + m và B = 2x – 3
b) A = x3 + 4x2 + 4x + m và B = x + 3
c) A = x3 – 13x + m và B = x2 + 4x + 3
d) A = x4 + 5x3 – x2 – 17x + m + 4 và B = x2 + 2x – 3
Bài 7: Cho các đa thức sau: A = x3 + 4×2 + 3x – 7, B = x + 4
a) Tính A : B
b) Tìm x ∈ Z sao cho A chia hết cho B.
Bài 8: Chứng minh:
a) x50 + x10 + 1 chia hết cho x20 + x10 + 1
b) x2012 + x2008 + 1 chia hết cho x2 + x + 1
Bài 9: Tìm thương Q và dư R sao cho A = B.Q + R biết.
a) A = x4 + 3x3 + 2x2 – x – 4 và B = x2 – 2x + 3
b) A = 2x3 – 3x2 + 6x – 4 và B = x2 – x + 3
c) A = 2x4 + x3 + 3x2 + 4x + 9 và B = x2 + 1
Bài 10: Tìm x, biết.
a) (8x2 – 4x) : (-4x) – (x + 2) = 8
b) (2x4 – 3x3 + x2) : (-x2) + 4(x – 1)2 = 0
B. Lý thuyết chia đa thức cho đơn thức
Quy tắc: Muốn chia đa thức A cho đơn thức B (trường hợp các hạng tử của đa thức A đều chia hết cho B) ta làm như sau:
– Chia lần lượt từng hạng tử của đa thức A cho đơn thức B;
– Cộng các kết quả tìm được lại với nhau.
Chú ý: Trong thực hành ta có thể nhẩm và bỏ bớt một số phép tính trung gian.
Ví dụ 1: (15x2y + 17xy3 – 6xy ) : 3xy
= (15x2y : 3xy) + (17xy3 : 3xy) – (6xy : 3xy)
Chú ý: Trường hợp đa thức A có thể phân tích thành nhân tử, ta thường phân tích A trước để rút gọn cho nhanh.
Ví dụ 2: (8x3 – 27y3) : (2x – 3y)
= (2x – 3y)(4x2 + 6xy + 9y2) : (2x – 3y)
= 4x2 + 6xy + 9y2.
Xem thêm