50 bài tập Những hằng đẳng thức đáng nhớ (có đáp án) - Toán 8

Bài tập Toán 8 Chương 1 Bài 3: Những hằng đẳng thức đáng nhớ

A. Bài tập Những hằng đẳng thức đáng nhớ

I. Bài tập trắc nghiệm

Bài 1: Điền vào chỗ trống: A = ( $\frac{1}{2}$ x – y )² = $\frac{1}{4}$ x² – … + y²

A. 2xy

B. xy

C. – 2xy

D. $\frac{1}{2}$ xy

Lời giải:

Áp dụng hằng đẳng thức (a – b)² = a² – 2ab + b².

Khi đó ta có A = ( $\frac{1}{2}$ x – y )² = $\frac{1}{4}$ x² – 2. $\frac{1}{2}$ x.y + y² = $\frac{1}{4}$ x² – xy + y².

Suy ra chỗ trống cần điền là xy.

Chọn đáp án B.

Bài 2: Giá trị của x thỏa mãn 2x² – 4x + 2 = 0 là ?

A. x = 1.

B. x = – 1.

C. x = 2.

D. x = – 2.

Lời giải:

Ta có 2x² – 4x + 2 = 0

⇔ 2( x² – 2x + 1 ) = 0 ( 1 )

Áp dụng hằng đẳng thức ( a – b )² = a² – 2ab + b²

Khi đó ta có ( 1 ) ⇔ 2( x – 1 )² = 0

⇔ x – 1 = 0

⇔ x = 1.

Chọn đáp án A.

Bài 3: Bài tập Những hằng đẳng thức đáng nhớ | Lý thuyết và Bài tập Toán 8 có đáp án

Lời giải:

Áp dụng hằng đẳng thức đáng nhớ: Bài tập Những hằng đẳng thức đáng nhớ | Lý thuyết và Bài tập Toán 8 có đáp án

Ta được:

Bài tập Những hằng đẳng thức đáng nhớ | Lý thuyết và Bài tập Toán 8 có đáp án

Chọn đáp án A

Bài 4: Rút gọn biểu thức: A = (x – 2y).(x² + 2xy + y²) – (x + 2y). (x² – 2xy + y²)

A. 2x³

B. -16y³

C. 16y³

D. –2x³

Lời giải:

Áp dụng hằng đẳng thức:

a³ – b³ = (a – b).(a² + ab + b²) và a³ + b³ = (a + b).(a² – ab + b²) ta được:

A = (x – 2y). (x² + 2xy + y²) – (x + 2y). (x² – 2xy + y²)

A = x³ – (2y)³ – [x³ + (2y)³]

A = x³ – 8y³ – x³ – 8y³ = -16y³

Chọn đáp án B

Bài 5: Rút gọn biểu thức A = (x + 2y ).(x – 2y) – (x – 2y)²

A. 2x² + 4xy

B. – 8y² + 4xy

C. – 8y²

D. – 6y² + 2xy

Lời giải:

Ta có: A = (x + 2y ). (x – 2y) – (x – 2y)²

A = x² – (2y)² – [x² – 2.x.2y +(2y)² ]

A = x² – 4y² – x² + 4xy – 4y²2

A = -8y² + 4xy

Chọn đáp án B

Bài 6: Chọn câu đúng

A. (c + d)² – (a + b)² = (c + d + a + b)(c + d – a + b)

B. (c – d)² – (a + b)² = (c – d + a + b)(c – d – a + b)

C. (a + b + c – d)(a + b – c + d) = (a + b)² – (c – d)²

D. (c – d)² – (a – b)² = (c – d + a – b)(c – d – a – b)

Lời giải:

Ta có:

(c + d)² – (a + b)² = (c + d + a + b)(c + d – (a + b)) = (c + d + a + b)(c + d – a – b) nên A sai

(c – d)² – (a + b)² = (c – d + a + b)[c – d – (a + b)] = (c – d + a + b)(c – d – a – b) nên B sai

(c – d)² – (a – b)² = (c – d + a – b)(c – d – (a – b)) = (c – d + a – b)(c – d – a + b) nên D sai

(a + b + c – d)(a + b – c + d) = [(a + b) + (c – d)][(a + b) – (c – d)] = (a + b)² – (c – d)² nên C đúng

Đáp án cần chọn là: C

Bài 7: Chọn câu đúng

A. 4 – (a + b)² = (2 + a + b)(2 – a + b)

B. 4 – (a + b)² = (4 + a + b)(4 – a – b)

C. 4 – (a + b)² = (2 + a – b)(2 – a + b)

D. 4 – (a + b)² = (2 + a + b)(2 – a – b)

Lời giải

Ta có 4 – (a + b)² = 2² – (a + b)²

= (2 + a + b)[2 – (a + b)]

= (2 + a + b)(2 – a – b)

Đáp án cần chọn là: D

Bài 8: Rút gọn biểu thức A = (3x – 1)² – 9x(x + 1) ta được

A. -15x + 1

B. 1

C. 15x + 1

D. – 1

Lời giải: Ta có

A = (3x – 1)² – 9x(x + 1)

= (3x)² – 2.3x.1 + 1 – (9x.x + 9x)

= 9x² – 6x + 1 – 9x² – 9x

= -15x + 1

Đáp án cần chọn là: A

Bài 9: Rút gọn biểu thức A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4), ta được:

A. 342

B. 243

C. 324

D. -324

Lời giải

Ta có

A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4)

= 5(x² + 2.x.4 + 16) + 4(x² – 2.x.5 + 5²) – 9(x² – 4²)

= 5(x² + 8x + 16) + 4(x² – 10x + 25) – 9(x² – 4²)

= 5x² + 40x + 80 + 4x² – 40x + 100 – 9x² + 144

= (5x² + 4x² – 9x²) + (40x – 40x) + (80 +100 + 144)

= 324

Đáp án cần chọn là: C

Bài 10: Rút gọn biểu thức B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7) ta được

A. 0

B. 1

C. 19

D. – 19

Lời giải

B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7)

= 2a² + 2a – 3a – 3 – (a² – 8a + 16) – (a² + 7a)

= 2a² + 2a – 3a – 3 – a² + 8a – 16 – a² – 7a

= – 19

Đáp án cần chọn là: D

Bài 11: Cho B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1). Chọn câu đúng.

A. B < 12

B. B > 13

C. 12 < B< 14

D. 11 < B < 13

Lời giải

B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1).

= (x²)² +2.x².4 + 3² – (x².x² + x².3) – 3(x² – 1)

= x⁴ + 6x² + 9 – x⁴ – 3x² – 3x² + 3 = 12

Đáp án cần chọn là: D

Bài 12: Cho Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án . Tìm mối quan hệ giữa C và D.

A. D = 14C + 1

B. D = 14C

C. D = 14C – 1

D. D = 14C – 2

Lời giải

Ta có:

Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án

Vậy D = 29; C = 2 suy ra D = 14C + 1 (do 29 = 14.2 + 1)

Đáp án cần chọn là: A

Bài 13: Cho M = 4(x + 1)² + (2x + 1)² – 8(x – 1)(x + 1) – 12x và N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14).

Tìm mối quan hệ giữa M và N

A. 2N – M = 60

B. 2M – N = 60

C. M> 0, N < 0

D. M > 0, N > 0

Lời giải

Ta có

M = 4(x + 1)² + (2x + 1)² – 8(x – 1)(x + 1) – 12

= 4(x² + 2x + 1) + (4x² + 4x + 1) – 8(x² – 1) – 12x

= 4x² + 8x + 4 + 4x² + 4x + 1 – 8x² +8 – 12x

= (4x² + 4x² – 8x²) + (8x + 4x – 12x) + 4 + 1 +8

= 13

N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14)

= 2(x² – 2x + 1) – 4(9 + 6x + x²) + 2x² + 28x

= 2x² – 4x + 2 – 36 – 24x – 4x² + 2x² + 28x

= (2x² +2x² – 4x²) + (-4x – 24x + 28x) + 2 – 36

= -34

Suy ra M = 13, N = -34 ⇔ 2M – N = 60

Đáp án cần chọn là: B

Bài 14: Có bao nhiêu giá trị x thỏa mãn (2x – 1)² – (5x – 5)² = 0

A. 0

B. 1

C. 2

D. 3

Lời giải

Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án

Vậy có hai giá trị của x thỏa mãn yêu cầu

Đáp án cần chọn là: C

Bài 15: Có bao nhiêu giá trị x thỏa mãn (2x + 1)² – 4(x + 3)² = 0

A. 0

B. 1

C. 2

D. 3

Lời giải

Ta có:

Trắc nghiệm Những hằng đẳng thức đáng nhớ có đáp án

Vậy có một giá trị của x thỏa mãn yêu cầu.

Đáp án cần chọn là: B

II. Bài tập tự luận

Bài 1: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a, $4{x^2} + 4x + 1$	b, $9{x^2} - 12x + 4$
c, $25{a^2} + 16{b^2} - 40ab$	d, ${x^2} - 3x + \frac{9}{4}$
e, ${\left( {x + 2} \right)^2} - 2.\left( {x + 2} \right) + 1$	f, ${\left( {{x^2} - 2x + 1} \right)^2} - 2.{\left( {x + 1} \right)^2}.4 + 16$

Lời giải:

a, $4{x^2} + 4x + 1 = {\left( {2x} \right)^2} + 2.2x.1 + 1 = {\left( {2x + 1} \right)^2}$

b, $9{x^2} - 12x + 4 = {\left( {3x} \right)^2} - 2.3x.2 + {2^2} = {\left( {3x - 2} \right)^2}$

c, $25{a^2} + 16{b^2} - 40ab = {\left( {5a} \right)^2} - 2.5a.4b + {\left( {4b} \right)^2} = {\left( {5a - 4b} \right)^2}$

d, ${x^2} - 3x + \frac{9}{4} = {x^2} - 2.\frac{3}{2}.x + {\left( {\frac{3}{2}} \right)^2} = {\left( {x - \frac{3}{2}} \right)^2}$

e, ${\left( {x + 2} \right)^2} - 2.\left( {x + 2} \right) + 1 = {\left( {x + 2 - 1} \right)^2} = {\left( {x + 1} \right)^2}$

f, $\begin{array}{l} {\left( {{x^2} - 2x + 1} \right)^2} - 2.{\left( {x + 1} \right)^2}.4 + 16 = \left( {{x^2} - 2x + 1 - 4} \right)\\ = \left[ {{{\left( {x - 1} \right)}^2} - 4} \right] = \left( {x - 1 - 2} \right)\left( {x - 1 + 2} \right) = \left( {x - 3} \right)\left( {x + 1} \right) \end{array}$

Bài 2: Tính giá trị của biểu thức:

a, ${\left( {a + b} \right)^2}$ tại a = 2, b = 3

b, ${\left( {a + b} \right)^2} - {\left( {a - b} \right)^2}$ tại $a = {2^8};b = {3^{10}}$

c, $24{x^2} - 480x + 2400$ tại x= 5

Lời giải:

a, Thay a = 2, b = 3 vào ${\left( {a + b} \right)^2}$ có: ${\left( {2 + 3} \right)^2} = {5^2} = 25$

b, Có ${\left( {a + b} \right)^2} - {\left( {a - b} \right)^2} = \left( {a + b - a + b} \right)\left( {a + b + a - b} \right) = 4ab$

Thay $a = {2^8};b = {3^8}$ có: ${4.2^8}{.3^{10}} = {2^2}{.2^8}{.3^{10}} = {2^{10}}{.3^{10}} = {\left( {2.3} \right)^{10}} = {6^{10}}$

c, Có $24{x^2} - 480x + 2400 = 24.\left( {{x^2} - 20x + 100} \right) = 24.{\left( {x - 10} \right)^2}$

Thay x = 5 có: $24.{\left( {5 - 10} \right)^2} = 24.{\left( { - 5} \right)^2} = 24.25 = 500$

Bài 3: Tính:

a, ${\left( {2a + b - 3c} \right)^2}$

b, ${\left( {a + 2b + 3c - 4d} \right)^2}$

Lời giải:

a, $\begin{array}{l} {\left( {2a + b - 3c} \right)^2} = {\left( {2a + b} \right)^2} - 2.3c.\left( {2a + b} \right) + {\left( {3c} \right)^2}\\ = 4{a^2} + 4ab + {b^2} - 12ac - 6bc + 9{c^2}\\ = 4{a^2} + {b^2} + 9{c^2} + 4ab - 12ac - 6bc \end{array}$

b, $\begin{array}{l} {\left( {a + 2b + 3c - 4d} \right)^2} = {\left( {a + 2b} \right)^2} + 2.\left( {a + 2b} \right).\left( {3c - 4d} \right) + {\left( {3c - 4d} \right)^2}\\ = {a^2} + 4ab + 4{b^2} + \left( {2a + 4b} \right)\left( {3c - 4d} \right) + 9{c^2} - 24cd + 16{d^2}\\ = {a^2} + 4ab + 4{b^2} + 6ac - 8ad + 12bc - 16bd + 9{c^2} - 24cd + 16{d^2} \end{array}$

Bài 4

Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) x²+ 2x + 1

b) 9x² + y² + 6xy;

c) 25a² + 4b² – 20ab;

d) x² – x + $\frac{1}{4}$

Đáp án và hướng dẫn giải:

a) x² + 2x + 1 = x²+ 2.x.1 + 12

= (x + 1)²

b) 9x² + y²+ 6xy = (3x)² + 2.3. x.y + y.2 = (3x + y)²

c) 25a² + 4b²– 20ab = (5a)² – 2.5a.2b + (2b)² = (5a – 2b)²

Hoặc 25a² + 4b² – 20ab = (2b)² – 2.2b.5a + (5a)² = (2b – 5a)²

d) x² – x + $\frac{1}{4}$

= x² – 2.x. $\frac{1}{2}$ + ( $\frac{1}{2}$ )²

=(x – $\frac{1}{2}$ )²

Hoặc x² – x + $\frac{1}{4}$

= $\frac{1}{4}$ – x + x2 =( $\frac{1}{2}$ )² – 2. $\frac{1}{2}$ x + x²= ( $\frac{1}{2}$ – x⁾²

Bài 5

Chứng minh rằng:

(10a + 5)² = 100a . (a + 1) + 25.

Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.

Áp dụng để tính: 25², 35², 65², 75².

Đáp án và hướng dẫn giải:

Ta có: (10a + 5)² = (10a)² + 2.10a.5 + 5²

= 100a² + 100a + 25

= 100a(a + 1) + 25.

Cách tính nhẩm bình thường của một số tận cùng bằng chữ số 5;

Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được

(10a + 5)² = 100a(a + 1) + 25

Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.

Áp dụng;

Để tính 25²ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.

Để tính 35² ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.

65² = (10.6 + 5)²= 100.6(6+1) +25= 600.7 +25 =4200 +25= 4225

75²=(10.7+5)2 = 100.7(7+1) +25 = 700.8 +25=5600 +25 = 5625

Bài 6

Hãy tìm cách giúp bạn An khôi phục lại những hằng đẳng thức bị mực làm nhòe đi một số chỗ:

a) x² + 6xy + … = (… + 3y)²;

b) … – 10xy + 25y² = (… – …)²;

Hãy nêu một số đề bài tương tự.

Đáp án và hướng dẫn giải:

a) x² + 6xy + … = (… + 3y)² nên x² + 2x . 3y + … = (…+3y)²

= x² + 2x . 3y + (3y)² = (x + 3y)²

Vậy: x² + 6xy +9y² = (x + 3y)²

b) …-2x . 5y + (5y)2 = (… – …)²;

x² – 2x . 5y + (5y)² = (x – 5y)²

Vậy: x² – 10xy + 25y² = (x – 5y)²

Bài 7:

Tính diện tích phần hình còn lại mà không cần đo.

Từ một miếng tôn hình vuông có cạnh bằng a + b, bác thợ cắt đi một miếng cũng hình vuông có cạnh bằng a – b (cho a > b). Diện tích phần hình còn lại là bao nhiêu? Diện tích phần hình còn lại có phụ thuộc vào vị trí cắt không?

Đáp án và hướng dẫn giải bài:

Diện tích của miếng tôn là (a + b)²

Diện tích của miếng tôn phải cắt là (a – b)².

Phần diện tích còn lại là (a + b)2 – (a – b)².

Ta có: (a + b)² – (a – b)² = a² + 2ab + b² – (a² – 2ab + b²)

= a² + 2ab + b² – a² + 2ab – b²

= 4ab

Vậy phần diện tích hình còn lại là 4ab và không phụ thuộc vào vị trí cắt.

Bài 8:

Nhận xét sự đúng, sai của kết quả sau:

x² + 2xy + 4y² = (x + 2y)²

Đáp án và hướng dẫn giải:

Nhận xét sự đúng, sai:

Ta có: (x + 2y)² = x² + 2 . x . 2y + 4y²

= x²+ 4xy + 4y²

Nên kết quả x² + 2xy + 4y² = (x + 2y)² sai.

Bài 9:

Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) 9x² – 6x + 1;

b) (2x + 3y)² + 2.(2x + 3y) + 1.

Hãy nêu một đề bài tương tự.

Đáp án và hướng dẫn giải:

a) 9x² – 6x + 1 = (3x)² – 2 . 3x . 1 + 1² = (3x – 1)²

Hoặc 9x² – 6x + 1 = 1 – 6x + 9x² = (1 – 3x)²

b) (2x + 3y) = (2x + 3y)² + 2 . (2x + 3y) . 1 + 1²

= [(2x + 3y) + 1]²

= (2x + 3y + 1)²

Đề bài tương tự. Chẳng hạn:

1 + 2(x + 2y) + (x + 2y)²

4x² – 12x + 9…

16x² y⁴ – 8xy² +1

Bài 10

Tính nhanh:

a) 1012; b) 1992; c) 47.53.

Đáp án và hướng dẫn giải:

a) 101² = (100 + 1)² = 100² + 2 . 100 + 1 = 10201

b) 199²= (200 – 1)² = 200² – 2 . 200 + 1 = 39601

c) 47.53 = (50 – 3)(50 + 3) = 50² – 3²= 2500 – 9 = 2491.

III. Bài tập vận dụng

Bài 1:

Chứng minh rằng:

(a + b)² = (a – b)² + 4ab;

(a – b)² = (a + b)² – 4ab.

Áp dụng:

a) Tính (a – b)², biết a + b = 7 và a . b = 12.

b) Tính (a + b)², biết a – b = 20 và a . b = 3.

Bài 2:

Tính giá trị của biểu thức 49x² – 70x + 25 trong mỗi trường hợp sau:

a) x = 5;

b) x = 1/7.

Bài 3:

Tính:

a) (a + b + c)²; b) (a + b – c)²;

c) (a – b – c)²

Bài 4. Áp dụng hằng đẳng thức để tính nhanh

a) $1001^{2}$ = b) 29,9. 30,1 =

c) $(31,8)^{2}$ – 2.31,8.21,8 + $(21,8)^{2}$ =

Bài 5. Điền vào ô trống để trở thành hằng đẳng thức:

Ví dụ : 36 $x^{2}$ + 24x + ………..=

Phân tích : 36 $x^{2}$ = $(6x)^{2}$ và 24x = 2. 6x. 2, từ đó phần còn thiếu là $2^{2}$ = 4

Đáp án : 36 $x^{2}$ + 24x + 4 = $(6x + 2)^{2}$

a) $x^{2}$ + 20x + …….. =

b) 16 $x^{2}$ + 24x + ……..=

c) $y^{2}$ – ………. + 49 =

d) …………- 42xy + 49 $y^{2}$ =

e) $x^{2}$ + ………..+ 4 $y^{4}$ =

f) 4 $x^{2}$ +…………..+ 1 =

g) (2a +3b)( – + ) = 8 $a^{3}$ + 27 $b^{3}$

h) (5x – )( + 20xy + ) = 125 $x^{3}$ – 64 $y^{3}$

Bài 6. Viết mỗi biểu thức sau dưới dạng tổng của hai bình phương

Ví dụ : $x^{2}$ – 2xy + 2 $y^{2}$ +2y +1 = ( $x^{2}$ – 2xy + $y^{2}$ ) + ( $y^{2}$ +2y +1) = $(x - y)^{2}$ + $(y + 1)^{2}$

a) $x^{2}$ + 10x + 26 + $y^{2}$ +2y =

b) $z^{2}$ – 6z + 13 + $t^{2}$ +4t =

c) 4 $x^{2}$ – 4xz + 1 + 2 $z^{2}$ -2z =

Bài 7. Tìm giá trị lớn nhất của biểu thức:

a) C = 4x – $x^{2}$ + 3

Tìm giá trị nhỏ nhất của biểu thức:

a) A = $x^{2}$ – 6x + 11

b) B = $x^{2}$ – 4x + $y^{2}$ – 8y + 6

Bài 8. Chứng minh các biểu thức sau luôn dương với mọi giá trị của biến

D = $x^{2}$ – 8x +19

Chứng minh các biểu thức sau luôn âm với mọi giá trị của biến

E = – $x^{2}$ + 2x – 7

Bài 9. Khai triển hằng đẳng thức dạng $(A + B)^{2}$ và $(A - B)^{2}$

$(A + B)^{2}$ = $A^{2}$ + 2.A.B + $B^{2}$ $(A - B)^{2}$ = $A^{2}$ – 2.A.B +

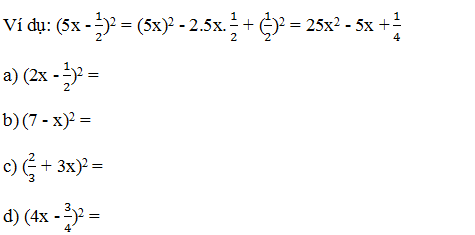
B. Lý thuyết Những hằng đẳng thức đáng nhớ

I. Lý thuyết

1. Bình phương của một tổng:

${(A + B)}^{2} = A^{2} + 2 A B + B^{2}$

2. Bình phương của một hiệu:

${(A - B)}^{2} = A^{2} - 2 A B + B^{2}$

3. Hiệu hai bình phương

$A^{2} - B^{2}$ = (A – B)(A + B)

II. Các dạng bài

1. Dạng 1: Thực hiện phép tính

a. Phương pháp giải:

Sử dụng trực tiếp các hằng đẳng thức đã học để khai triển các biểu thức

b, Ví dụ minh họa:

VD1: Thực hiện phép tính:

Những hằng đẳng thức đáng nhớ lớp 8 và cách giải các dạng bài tập – Toán lớp 8 (ảnh 1)

VD2: Viết các biểu thức sau dưới dạng bình phương một tổng hoặc bình phương một hiệu:

a, $4 x^{2} + 4 x + 1$

b, $x^{2} - 8 x + 16$

Giải:

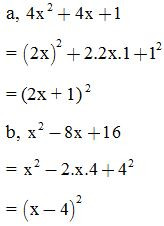
Những hằng đẳng thức đáng nhớ lớp 8 và cách giải các dạng bài tập – Toán lớp 8 (ảnh 1)

2. Dạng 2: Chứng minh các đẳng thức

a. Phương pháp giải:

Áp dụng linh hoạt các hằng đẳng thức, lựa chọn vế có thể dễ dàng áp dụng các hằng đẳng thức.

b. Ví dụ minh họa:

Chứng minh các đẳng thức sau:

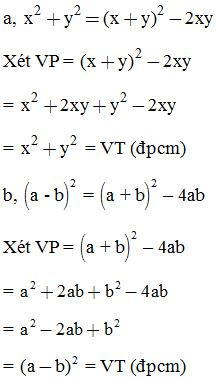
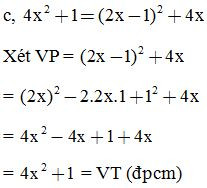
Những hằng đẳng thức đáng nhớ lớp 8 và cách giải các dạng bài tập – Toán lớp 8 (ảnh 1)

3. Dạng 3: Tính nhanh

a. Phương pháp giải:

Áp dụng linh hoạt các hằng đẳng thức cho các số tự nhiên

b. Ví dụ minh họa:

Tính nhanh:

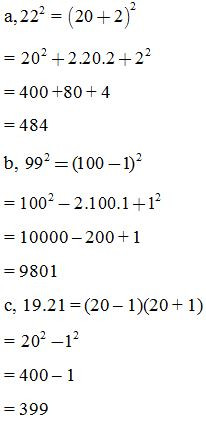
Những hằng đẳng thức đáng nhớ lớp 8 và cách giải các dạng bài tập – Toán lớp 8 (ảnh 1)

4. Dạng 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức

a. Phương pháp giải:

Sử dụng các hằng đẳng thức và cần chú ý:

$A^{2} \geq 0$ và $- A^{2} \leq 0$

b. Ví dụ minh họa:

a, Chứng minh $9 x^{2} - 6 x + 3$ luôn dương với mọi x

Giải:

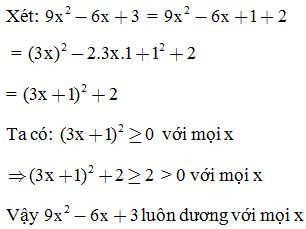
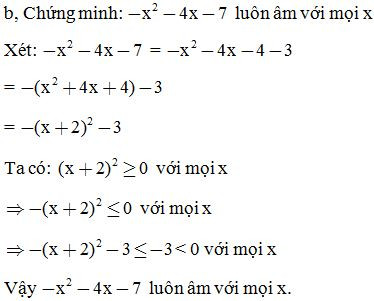
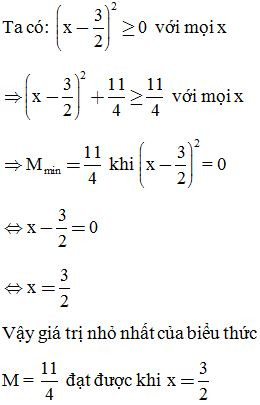
Những hằng đẳng thức đáng nhớ lớp 8 và cách giải các dạng bài tập – Toán lớp 8 (ảnh 1)

Xem thêm

Bài 5

Bài 6

Bài liên quan:

Leave a Comment Hủy