Lý thuyết Toán lớp 6 Bài 2: Xác suất thực nghiệm
Video giải Toán 6 Bài 2: Xác suất thực nghiệm – Chân trời sáng tạo
A. Lý thuyết Xác suất thực nghiệm
1. Khả năng xảy ra của một sự kiện
Khi thực hiện một phép thử nghiệm, một sự kiện có thể xảy ra hoặc không thể xảy ra. Để nói về khả năng xảy ra của mỗi sự kiện, ta dùng một con số có giá trị từ 0 đến 1.
Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.
Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.
Ví dụ 1. Trong hộp có 3 quả bóng: bóng xanh, bóng đỏ và bóng vàng. Không nhìn vào hộp, chọn ra từ hộp một quả bóng. Xét khả năng xảy ra của mỗi sự kiện sau:
a) Bóng chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng;
b) Bóng chọn ra có màu tím.
Lời giải:
a) Khi chọn một quả bóng từ hộp thì quả bóng được chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng.
Do đó, sự kiện này chắc chắn xảy ra.
Vậy sự kiện “Bóng chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng” có khả năng xảy ra bằng 1.
b) Vì ba quả trong hộp không có quả bóng nào có màu tím nên sự kiện “Bóng chọn ra có màu tím” không xảy ra.
Vậy sự kiện “Bóng chọn ra có màu tím” có khả năng xảy ra bằng 0.
2. Xác suất thực nghiệm
Thực hiện lặp đi lặp lại một hoạt động nào đó n lần. Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số
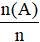= Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
được gọi là xác suất thực nghiệm của sự kiện A sau n hoạt động vừa thực hiện.
Ví dụ 2. Tung hai đồng xu cân đối 40 lần ta được kết quả như sau:
|
Sự kiện |
Hai đồng sấp |
Một đồng sấp, một đồng ngửa |
Hai đồng ngửa |
|
Số lần |
12 |
15 |
13 |
Hãy tính xác suất thực nghiệm của sự kiện:
a) Hai đồng xu sấp.
b) Có một đồng xu sấp, một đồng xu ngửa.
Lời giải:
a) Xác suất thực nghiệm của sự kiện “Hai đồng xu sấp” tung 40 lần tung là:
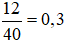
b) Xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” tung 30 lần tung là:
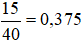
B. Bài tập tự luyện
Bài 1. Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
8 |
6 |
10 |
9 |
8 |
9 |
Hãy tính xác suất thực nghiệm của sự kiện:
a) Gieo được mặt có 5 chấm.
b) Gieo được mặt có số chẵn chấm.
Lời giải:
a) Số lần xuất hiện mặt 5 chấm của con xúc xắc 6 mặt trong 50 lần gieo là: 8.
Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có 5 chấm” là: 
.
b) Số mặt có chẵn chấm là các mặt có 2 chấm, 4 chấm và 6 chấm.
Số lần xuất hiện mặt 2 chấm là: 6.
Số lần xuất hiện mặt 4 chấm là: 9.
Số lần xuất hiện mặt 6 chấm là: 9.
Do đó, số lần xuất hiện mặt có chẵn chấm của con xúc xắc 6 mặt trong 50 lần gieo là: 6 + 9 + 9 = 24.
Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có số chẵn chấm” là: 
Bài 2. Trong hộp có một số viên bi màu xanh, đỏ và vàng có kích thước giống nhau. Lấy ngẫu nhiên một viên bi từ hộp, xem màu rồi trả lại lại. Lặp lại hoạt động đó 80 lần ta được kết quả như sau:
|
Loại bi |
Bi xanh |
Bi đỏ |
Bi vàng |
|
Số lần |
22 |
45 |
13 |
a) Tính xác suất thực hiện của sự kiện “lấy được viên bi xanh”.
b) Em hãy dự đoán xem trong hộp loại bi nào có nhiều hơn.
Lời giải:
a) Số lần lấy được bi xanh trong 80 lần lấy bi từ hộp là 22.
Vậy xác suất thực nghiệm của sự kiện “lấy được viên bi xanh” trong 80 lần lấy là: 
b) Tổng số viên bi xanh và viên bi vàng là: 22 + 13 = 35 (viên bi)
Ta thấy: số lần lấy được viên bi đỏ nhiều hơn so với số lần lấy được viên bi xanh và viên bi vàng.
Vậy có thể dự đoán là trong hộp đó số viên bi đỏ nhiều hơn số viên bi đỏ và số viên bi vàng.
Bài 3. Số điện thoại một cửa hàng bán được trong 30 ngày của tháng 8 được cho ở bảng sau:
|
5 |
7 |
4 |
5 |
5 |
3 |
5 |
3 |
6 |
7 |
|
4 |
7 |
8 |
5 |
2 |
7 |
3 |
6 |
4 |
12 |
|
5 |
8 |
6 |
4 |
9 |
5 |
8 |
9 |
5 |
5 |
Hãy tính xác suất thực nghiệm của sự kiện:
a) Cửa hàng bán được 5 chiếc điện thoại một ngày.
b) Cửa hàng bán được trên 7 chiếc điện thoại một ngày.
Lời giải:
a) Số ngày cửa hàng bán được 5 chiếc điện thoại trong 30 ngày là 9.
Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được 5 chiếc điện thoại một ngày” là: 
.
b) Số ngày cửa hàng bán được trên 7 chiếc điện thoại bằng tổng số các ngày cửa hàng bán được 8 chiếc điện thoại, 9 chiếc điện thoại và 12 chiếc điện thoại.
Số ngày cửa hàng bán được 8 chiếc điện thoại là: 3.
Số ngày cửa hàng bán được 9 chiếc điện thoại là: 2.
Số ngày cửa hàng bán được 12 chiếc điện thoại là: 1.
Số ngày cửa hàng bán được trên 7 chiếc điện thoại một ngày trong 30 ngày là:
3 + 2 + 1 = 6.
Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được trên 7 chiếc điện thoại một ngày” là: 
Xem thêm các bài tóm tắt lý thuyết Toán 6 Chân trời sáng tạo hay, chi tiết khác:
Lý thuyết Bài 5: Trung điểm của đoạn thẳng
Lý thuyết Bài 6: Góc
Lý thuyết Bài 7: Số đo góc. Các góc đặc biệt
Lý thuyết Bài 1: Phép thử nghiệm – Sự kiện
Lý thuyết Bài 2: Xác suất thực nghiệm