Bộ 8 Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận

Đề thi Toán lớp 11 học kì 2 có ma trận năm 2022 (8 đề)

Ma trận đề

Nội dung kiến thức	Đơn vị kiến thức	Mức độ nhận thức								Tổng			% tổng điểm
		Nhận biết		Thông hiểu		Vận dụng		Vận dụng cao
										Số CH		Thời gian
		Số CH	Thời gian	Số CH	Thời gian	Số CH	Thời gian	Số CH	Thời gian	TN	TL
Giới hạn	Giới hạn của dãy số	5	5	2	4	1	8	1	12	23	3	63	66
	Giới hạn của hàm số
	Hàm số liên tục
Đạo hàm	Định nghĩa và ý nghĩa của đạo hàm	1	1	1	2			1	12
	Quy tắc tính đạo hàm	6	6	2	4
	Đạo hàm của hàm số lượng giác	3	3	3	6
	Đạo hàm cấp hai			2	4					2		4	4
Vectơ trong không gian. Quan hệ vuông góc trong không gian.	Vectơ trong không gian	1	1			1	8			10	1	23	30
	Hai đường thẳng vuông góc	1	1	1	2
	Đường thẳng vuông góc với mặt phẳng	1	1	2	4
	Hai mặt phẳng vuông góc	1	1	1	2
	Khoảng cách	1	1	1	2
Tổng		20		15		2		2		35	4	90	100
Tỉ lệ (%)		40		30		20		10
Tỉ lệ chung (%)		70				30

 

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 1

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 1)

I. TRẮC NGHIỆM (3,0 điểm)

Chọn phương án trả lời đúng cho các câu hỏi sau:

Câu 1. Cho hàm số \(f(x) = \sqrt {2{x^2} – 4x + 5} \) . Khẳng định nào dưới đây đúng?

A. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) =  – \infty \].

B. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) =  + \infty \].

C. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) = 2\].

D. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) =  – 2\].

Câu 2. Hàm số \(y = {\cos ^2}3x\) có đạo hàm là

A. \(y’ = 6\sin 6x.\)

B. \(y’ = 2\cos 3x.\)

C. \(y’ =  – 3\sin 6x.\)

D. \(y’ =  – 3\sin 3x.\)

Câu 3. Trong không gian, cho đoạn thẳng AB có trung điểm là I, \((\alpha )\) là mặt phẳng trung trực của đoạn thẳng AB. Phát biểu nào sau đây đúng ?

A.  \((\alpha )\) qua I và vuông góc với AB.

B.  \((\alpha )\) qua A và vuông góc với AB.

C.  \((\alpha )\) qua I và không vuông góc với AB.

D.  \((\alpha )\) qua B và vuông góc với AB.

Câu 4: Cho hai hàm số \(f\left( x \right),g\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) =  – 5\) và \(\mathop {\lim }\limits_{x \to 1} g\left( x \right) = 2.\) Giá trị của \(\mathop {\lim }\limits_{x \to 1} \left[ {f\left( x \right) – g\left( x \right)} \right]\) bằng

A. 7.

B. 3.

C.  -7.

D. -3.

Câu 5: Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA vuông góc với mặt phẳng (ABCD) (như hình vẽ minh hoạ). Hãy chọn khẳng định đúng.

A.  \[BD \bot (SAC)\].

B.  \[CD \bot (SAD)\].   

C.  \[AC \bot (SBD)\]

D. \[BC \bot (SAB)\].

Câu 6. Cho hình chóp S.ABCD có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.

A.  \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} .\)

B.  \(\overrightarrow {SA}  + \overrightarrow {AB}  = \overrightarrow {SD}  + \overrightarrow {DC} .\)                             

C.  \(\overrightarrow {SA}  + \overrightarrow {AD}  = \overrightarrow {SB}  + \overrightarrow {BC} .\)

D.  \(\overrightarrow {SA}  + \overrightarrow {SB}  = \overrightarrow {SC}  + \overrightarrow {SD} .\)

Câu 7. Cho các hàm số u(x); v(x) có đạo hàm trên khoảng K và \[v\left( x \right) \ne 0\] với mọi \[x \in K\]. Mệnh đề nào sau đây SAI?

A. \[{\left[ {\frac{{u\left( x \right)}}{{v\left( x \right)}}} \right]^\prime } = \frac{{u’\left( x \right).v\left( x \right) – u\left( x \right).v’\left( x \right)}}{{{v^2}\left( x \right)}}\]

B. \[{\left[ {u\left( x \right) + v\left( x \right)} \right]^\prime } = u’\left( x \right) + v’\left( x \right)\]

C. \[{\left[ {u\left( x \right).v\left( x \right)} \right]^\prime } = u’\left( x \right).v’\left( x \right)\]

D. \[{\left[ {u\left( x \right) – v\left( x \right)} \right]^\prime } = u’\left( x \right) – v’\left( x \right)\]

Câu 8. Cho \[n \in N,n > 1\] , tính đạo hàm của hàm số \[y = {x^n}\].

A. \[y’ = n.{x^n}\]

B. \[y’ = n.{x^{n – 2}}\]

C. \[y’ = 2n.{x^{n – 1}}\]

Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông, cạnh SA vuông góc với mặt phẳng (ABCD), (xem hình vẽ).  Góc giữa đường thẳng SB và mặt phẳng (ABCD) là góc

A. \[\widehat {SBD}\]

B. \[\widehat {SBA}\]

C. \[\widehat {S{\rm{D}}C}\]

D. \[\widehat {SBC}\]

Câu 10.  Cho hàm số \(y = {x^7}\). Đẳng thức nào dưới đây đúng?

A. \(y” = 42{x^5}\).

B. \(y” = 14{x^6}\).

C. \(y” = 7{x^5}\).

D. \(y” = 7{x^6}\).

Câu 11. Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 7 cm. Tính khoảng cách từ điểm B đến mặt phẳng (CDD’).

A. \(7\sqrt 3 \) cm.

B. 7 cm.

C. 14 cm.

D. \(7\sqrt 2 \) cm.

Câu 12: Tính đạo hàm của hàm số \(f(x) = {x^{2021}}\) .

A. \(f'(x) = 2021{x^{2022}}\).

B. \(f'(x) = 2021{x^{2020}}\).

C. \(f'(x) = 2021x\).

D. \(f'(x) = 2021{x^{2021}}\).

Câu 13:  Giả sử u = u(x). Khi đó đẳng thức nào sau đây đúng?

A. \({\left( {{u^n}} \right)^\prime } = {u^{n – 1}}.u’\,\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

B. \({\left( {{u^n}} \right)^\prime } = n.{u^{n – 1}}\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

C. \({\left( {{u^n}} \right)^\prime } = n.u’\,\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

D. \({\left( {{u^n}} \right)^\prime } = n.{u^{n – 1}}.u’\,\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

Câu 14:  Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\). Khi đó đẳng thức nào dưới đây là sai?

 

A. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) – g\left( x \right)} \right] = L – M\).

B. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\).

C. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right)g\left( x \right)} \right] = L + M\).

D. \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{L}{M},\,\,\,\left( {M \ne 0} \right)\).

Câu 15: Cho một vật chuyển động theo phương trình \(S = {t^3} + m{t^2} + 10t + {m^2}\), trong đó t được tính bằng giây, S được tính bằng mét và m là tham số thực. Biết tại thời điểm t = 4s vận tốc của vật bị triệt tiêu. Gọi a là gia tốc của vật tại thời điểm t = 5s. Chọn khẳng định đúng trong các khẳng định sau

A. \(a \in \left( {30;40} \right)\).

B. \(a \in \left( {20;30} \right)\).

C. \(a \in \left( {0;10} \right)\).

D. \(a \in \left( {10;20} \right)\).

II. Tự luận (7 điểm)

Câu 1. Tính các giới hạn sau:

a) \(\lim \frac{{5n + 2}}{{3n – 1}}.\)

b) \[\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {x + 3}  – 2}}{{x – 1}}.\] 

Câu 2. Cho hàm số \[y = f(x) = \left\{ \begin{array}{l}\frac{{{x^2} – 3x + 2}}{{x – 2}}{\rm{     khi  }}x \ne 2\\3 – a{\rm{                 khi  }}x = 2\end{array} \right..\]

Tìm điều kiện của tham số a để hàm số trên gián đoạn tại điểm x = 2.

Câu 3. Cho hàm số \[y = f(x) = \frac{1}{3}{x^3} – 2x\], có đồ thị (C)

a) Tính đạo hàm của hàm số trên.

 b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm có hoành độ x₀ =3

Câu 4. Cho hình chóp S.ABC có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S lên mặt đáy là trung điểm M của cạnh AD, \(SM = \frac{{a\sqrt 3 }}{2}.\) Gọi N, Q  lần lượt là trung điểm của các cạnh SC; SB

a) Chứng minh rằng \(CD \bot \left( {SAD} \right).\)

b) Chứng minh rằng \(\left( {SBC} \right) \bot \left( {SMQ} \right).\)

c) Xác định và tính cosin của góc giữa hai mặt phẳng (AND) và (SBC)

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 2

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 2)

I. TRẮC NGHIỆM (3,0 điểm)

Chọn phương án trả lời đúng cho các câu hỏi sau:

Câu 1. Hệ số góc của tiếp tuyến với đồ thị hàm số \[y = {x^3} – 4{x^2} + 1\] tại điểm có hoành độ bằng 1 là

A. -5.

B. 5.                                     

C. 4.                                     

D. \( – 4\).

Câu 2. Cho hàm số \(f(x) = \sqrt {3{x^2} – 4x + 5} \) . Khẳng định nào dưới đây đúng?

A. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) =  – \infty \].

B. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) =  + \infty \].

C. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) = 3\].

D. \[\mathop {\lim }\limits_{x \to  – \infty } f(x) =  – 3\].

Câu 3. Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} – 1}}{{x – 1}}\,\,\,\,\,khi\,\,\,\,x \ne 1\\m + 2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,\,\,x = 1\end{array} \right.\) liên tục tại điểm \({x_0} = 1\).  

A.  m = 3.

B. m = 0.

C. m = 4.

D. m = 1.

Câu 4. Tính đạo hàm của hàm số sau \(y = \frac{{ – 3x + 4}}{{x – 2}}\).

A. \(y’ = \frac{2}{{{{(x – 2)}^2}}}\).

B. \(y’ = \frac{{ – 11}}{{{{(x – 2)}^2}}}\).

C. \(y’ = \frac{{ – 5}}{{{{(x – 2)}^2}}}\).

D. \(y’ = \frac{{10}}{{{{(x – 2)}^2}}}\).

Câu 5. Nếu \[\mathop {\lim }\limits_{x \to 0} f\left( x \right) = 5\] thì \(\mathop {\lim }\limits_{x \to 0} \left[ {3x – 4f\left( x \right)} \right]\) bằng bao nhiêu?

A. -17.

B. -1.                                    

C. 1.                                     

D. -20.

Câu 6. Cho hàm số \(f\left( x \right) = \frac{1}{3}{x^3} – \left( {m – 2} \right){x^2} – \left( {2m – 3} \right)x + 2020\), m là tham số. Biết rằng tồn tại giá trị \[{m_0}\] sao cho \(f’\left( x \right) \ge 0\),\(\forall x \in \mathbb{R}\). Khi đó \[{m_0}\] thuộc khoảng nào sau đây?

A. (0; 2).

B. (-3; 1).

C. (3; 6).

D. (-4; -2).

Câu 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O. Biết rằng SA = SC; SB = SD. Khẳng định nào sau đây đúng?

A. \(CD \bot AD\).

B. \(CD \bot (SBD)\).

C. \(AB \bot (SAC)\).

D. \(SO \bot (ABCD)\)

Câu 8. Một chất điểm chuyển động thẳng xác định bởi công thức \[v\left( t \right) = 8t + 3{t^2}\], t tính bằng giây, v(t) tính bằng (m/s). Tính gia tốc của chất điểm khi vận tốc đạt \[11\](m/s).

A.\[20\].                               

B.\[14\].

C.\[2\].

D. 11.

Câu 9. Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây?

A. (SBC).

B. (SAC).

C. (SBD).

D. (ABCD).

Câu 10. Hàm số \(y = {\cos ^2}3x\) có đạo hàm là

A. \(y’ = 6\sin 6x.\)

B. \(y’ = 2\cos 3x.\)

C. \(y’ =  – 3\sin 6x.\)

D. \(y’ =  – 3\sin 3x.\)

Câu 11. Cho \(\mathop {\lim }\limits_{x \to 1} \left( {\frac{{\sqrt {{x^2} + x + 2}  – \sqrt[3]{{3x + 5}}}}{{{x^2} – 3x + 2}}} \right) = \frac{a}{b}\,\)(\(\frac{a}{b}\) là phân số tối giản; a, b là số nguyên). Tính tổng \(P = {a^2} + {b^2}\).

A. P = 5.

B. P = 3.

C. P = 2.

D. P = -2.

Câu 12. Cho hình chóp S.ABCD  có đáy ABCD  là hình vuông cạnh 2a, \(SA \bot (ABCD)\)  Khoảng cách từ  điểm D đến mặt phẳng (SAC) bằng

A. \(a\sqrt 2 \).

B. a.                                     

C. \(\frac{{2a\sqrt 2 }}{3}\).

D. \(\frac{{a\sqrt 2 }}{2}\).

II. TỰ LUẬN (7,0 điểm)

Câu 13. (3,0 điểm)

1) Tính các giới hạn sau:          

a) \(\mathop {\lim }\limits_{x \to 4} \frac{{2{x^2} – 7x – 4}}{{x – 4}}\).

b) \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} + x}  – \sqrt {{x^2} + 1} } \right)\).

2) Tính đạo hàm của các hàm số sau: 

a) \(y = \frac{1}{2}{x^4} + 2\sqrt x \) với x > 0.                      

b) \[y = 2\sin x + \sqrt 3 x\].

Câu 14. (1,0 điểm) Cho hàm số \(y = \frac{1}{3}{x^3} – 3x + 1\) có đồ thị là (C). Viết phương trình tiếp tuyến của (C) tại điểm có tung độ bằng 3.

Câu 15. (2,5 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh a. Mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi H; K lần lượt là trung điểm của AB; BC.

a) Chứng minh rằng \(SH \bot \left( {ABCD} \right)\) và \(\left( {SAD} \right) \bot \left( {SAB} \right)\).

b) Gọi \[\varphi \] là góc giữa đường thẳng SC và mặt phẳng (ABCD). Tính \[\tan \varphi \].

c) Tính khoảng cách từ K đến (SAD).

Câu 16. (0,5 điểm) Cho hàm số \[f(x) = a{x^3} + b{x^2} + cx + d\left( {a \ne 0} \right)\] có đồ thị là (C). Biết (C) cắt trục hoành tại 3 điểm phân biệt có hoành  độ \[{x_1},{x_2},{x_3}\]. Tính giá trị biểu thức \[D = \frac{1}{{f’\left( {{x_1}} \right)}} + \frac{1}{{f’\left( {{x_2}} \right)}} + \frac{1}{{f’\left( {{x_3}} \right)}}\].

 

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 3

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 3) 

I. Trắc nghiệm (6 điểm)

Câu 1: Hàm số nào sau đây không liên tục trên R?

A. \[y = \sin x\].

B. \[y = 3{x^4} – 2x + 3\].

C. \[y = \tan x\].

D. \[y = \cos x\].

Câu 2: Tính\[\mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^2} – 1}}{{{x^2} + 3x + 2}}\] bằng

A. 1.

B. \[\frac{1}{2}\].        

C. -1.                           

D. \[ – \frac{1}{2}\].

Câu 3: Tính \[\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1}  – 2}}{{9 – {x^2}}}\]    bằng

A. \[ – \frac{1}{{24}}\].

B. \[\frac{1}{{24}}\].

C. \[\frac{1}{6}\].

D. \[ – \frac{1}{6}\].

Câu 4: Chứng minh rằng phương trình \[{x^3} – x + 3 = 0\]có ít nhất một nghiệm.

Một bạn học sinh trình bày lời giải như sau:

Bước 1:  Xét hàm số \[y = f(x) = {x^3} – x + 3\] liên tục trên \[\mathbb{R}\].

Bước 2:  Ta có  f(0) = 3và  f(-2) = -3.

Bước 3:  suy ra  f(0).f(-2) > 0.

Bước 4:  Vậy phương trình đã cho có ít nhất 1 nghiệm.

Hãy tìm bước giải sai của bạn học sinh trên ?

A. Bước 1.

B. Bước 2 .

C. Bước 3.

D. Bước 4 .

Câu 5: Đạo hàm của hàm số \[y = {\rm{cos}}2x\] tại \[x = \frac{\pi }{8}\] là

A.\[\sqrt 2 \].

B.\[\frac{{\sqrt 2 }}{2}\].

C.\[ – {\rm{ }}\sqrt 2 \].

D. \[ – {\rm{ }}\frac{{\sqrt 2 }}{2}\].

Câu 6: Khẳng định nào sau đây sai?

A. \({\left( {\sin x} \right)^\prime } = \cos x\).

B. \({\left( {\cos x} \right)^\prime } =  – \sin x\).

C. \[{\left( {\tan x} \right)^\prime } =  – \frac{1}{{{\rm{co}}{{\rm{s}}^2}x}}\] .

D. \({\left( {\cot x} \right)^\prime } =  – \frac{1}{{{\rm{si}}{{\rm{n}}^2}x}}\).

Câu 7: Cho \[u = u\left( x \right),v = v\left( x \right),v\left( x \right) \ne 0\]. Hãy chọn khẳng định sai?

A.\[\left( {u + v} \right)’ = u’ + v’\].

B.\[{\left( {\frac{1}{v}} \right)^\prime } =  – \frac{{v’}}{{{v^{}}}}\].               

 C.\[\left( {u.v} \right)’ = u’.v + u.v’\].

D.\[{\left( {k.u} \right)^\prime } = k.u’\].

Câu 8: Tính đạo hàm của hàm số sau \[y = \sqrt {{{\left( {2x + 1} \right)}^{2017}}} \].

A.\[y’ = \frac{{2017}}{{2\sqrt {{{\left( {2x + 1} \right)}^{2017}}} }}\]

B.\[y’ = \frac{{2017{{\left( {2x + 1} \right)}^{2016}}}}{{2\sqrt {{{\left( {x + 1} \right)}^{2017}}} }}\].                       

 C.\[y’ = \frac{{{{\left( {2x + 1} \right)}^{2017}}}}{{2\sqrt {{{\left( {2x + 1} \right)}^{2017}}} }}\].

 D.\[y’ = \frac{{2017{{\left( {2x + 1} \right)}^{2016}}}}{{\sqrt {{{\left( {2x + 1} \right)}^{2017}}} }}\] .

Câu 9:  Đạo hàm của hàm số \(y = \frac{{2x – 1}}{{1 – x}}\) là

A. \(y’ = \frac{1}{{{{\left( {x – 1} \right)}^2}}}\).

B. \(y’ = \frac{{ – 1}}{{{{\left( {1 – x} \right)}^2}}}\).

C. \(y’ = \frac{3}{{{{\left( { – x + 1} \right)}^2}}}\).

D. \(y’ = \frac{{ – 3}}{{{{\left( {1 – x} \right)}^2}}}\).

Câu 10: Đạo hàm của hàm số \[y = {x^3}{\rm{cos}}x\]là

A. \[y’ = 3{x^2}\cos x – {x^3}\sin x\].

B. \[y’ = 3{x^2}\cos x + {x^3}\sin x\].

C. \[y’ = 3x\cos x – {x^3}\sin x\].

D. \[y’ = 3{x^2}\cos x + 3{x^2}\sin x\].

Câu 11: Đạo hàm cấp hai của  hàm số \[y = \cos x\] là  

 A.\[y” =  – \sin x\].

B.\[y” =  – \cos x\].

C.\[y” = \cos x\].

D. \[y” = \sin x\].

Câu 12: Cho hình hộp ABCD.A’B’C’D’. Đẳng thức nào sau đây là sai?

A. \[\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA’}  = \overrightarrow {AC’} \].

B. \[\overrightarrow {BC}  + \overrightarrow {CD}  + \overrightarrow {BB’}  = \overrightarrow {BD’} \].                               

C. \[\overrightarrow {CB}  + \overrightarrow {CD}  + \overrightarrow {{\rm{DD’}}}  = \overrightarrow {CA’} \].

D. \[\overrightarrow {AD}  + \overrightarrow {AB}  + \overrightarrow {AA’}  = \overrightarrow {A’C} \].

Câu 13: Cho hình lập phương  ABCD.A’B’C’D’. Tìm góc giữa hai vectơ \(\overrightarrow {AD’} \) và \(\overrightarrow {BD} \).

 A. 45⁰

B. 30⁰

C. 60⁰

D. 120⁰

Câu 14: Trong không gian, phát biểu nào sau đây là sai ?

A. Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song với nhau.

B. Nếu hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song với nhau.

C. Cho hai đường thẳng song song. Đường thẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

D. Hai đường thẳng vuông góc với nhau thì chúng có thể cắt nhau hoặc chéo nhau.

Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, \[SA \bot (ABC)\] và  AH là đường cao của \(\Delta SAB\). Khẳng định nào sau đây sai ?

A. \[SB \bot BC\].

B. \(AH \bot BC\).

C. \(SB \bot AC\).

D. \(AH \bot SC\).

Câu 16: Cho hình chóp S.ABCD có đáy ABCD là hình vuông  và \[SA \bot (ABCD)\]. Chọn khẳng định sai ?

A. \(BD \bot \left( {SAC} \right)\).

B. \(AC \bot \left( {SBD} \right)\).

C. \(BC \bot \left( {SAB} \right)\).

D.\(DC \bot \left( {SAD} \right)\).

Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và \[SA \bot (ABCD)\]. Khi đó, mặt phẳng (SDC) vuông góc với mặt phẳng

A. (SBC).

B. (SAC).

C. (SAD).  

D. (ABCD).

Câu 18: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \[SA \bot (ABCD)\] và  SA = x. Tìm x để góc giữa hai mặt phẳng (SBC) và (ABCD) bằng  60⁰ là

A. \(x = \frac{{a\sqrt 3 }}{3}\).

B. \(x = a\sqrt 3 \).

C. \(x = a\sqrt 6 \).

D. \(x = a\sqrt 2 \).

Câu 19: Một vật được thả rơi tự do ở độ cao 147m có phương trình chuyển động \(S\left( t \right) = \frac{1}{2}g{t^2}\), trong đó\(g = 9,8m/{s^2}\)và  t tính bằng giây (s). Tính vận tốc của vật tại thời điểm vật tiếp đất.  

A. 30 m/s

B. \(\sqrt {30} {\rm{ }}m/s\)

C. \(\frac{{49\sqrt {30} }}{5}m/s\)

D. \(\frac{{49\sqrt {15} }}{5}m/s\)

Câu 20: Cho a và b là hai đường thẳng chéo nhau, biết \(a \subset (P),b \subset (Q)\) và\((P)//(Q)\). Khẳng định nào sau đây là sai?

A. Khoảng cách giữa hai đường thẳng a và b bằng khoảng cách từ đường thẳng a đến mặt phẳng (Q).

B. Khoảng cách giữa hai đường thẳng  a và b bằng khoảng cách từ một điểm A tùy ý thuộc đường thẳng a đến mặt phẳng (Q).

C. Khoảng cách giữa hai đường thẳng a và b không  bằng khoảng cách giữa hai mặt phẳng (P) và (Q).

D. Khoảng cách giữa hai đường thẳng a và b bằng độ dài đoạn thẳng vuông góc chung của chúng.

II. Phần tự luận (4,0 điểm):

Bài 1( 0,5 điểm): Viết phương trình tiếp tuyến của  đồ thị hàm số  \[(C):y = \frac{{x – 3}}{{x + 2}}\], biết tiếp tuyến song song với đường thẳng \[d:y = x – 2017\].

Bài 2 ( 1,5 điểm): Tính đạo hàm của các hàm số sau: 

a) \(y =  – \frac{{{x^5}}}{{15}} + 2{x^2} – \sqrt x \).

b) \(y = \frac{{\cos x}}{{\sin x – \cos x}}\).

c) \[y = {\rm{co}}{{\rm{s}}^2}\left( {2x – \frac{\pi }{3}} \right)\].

Bài 3 ( 2,0 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, \(SA \bot \left( {ABCD} \right)\)và  \(SA = 2a\sqrt {10} \). Gọi M , N lần lượt là trung điểm của BC và CD.

a. Chứng minh : \[BD \bot (SAC)\]

b. Tính góc giữa SM và (ABCD).

c. Tính khoảng cách từ điểm C đến mặt phẳng (SMN).

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 4

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 4)

I. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1: Cho hai dãy \(\left( {{u_n}} \right)\) và \(\left( {{v_n}} \right)\) thỏa mãn \(\lim {u_n} = 2\) và \(\lim {v_n} = 3.\) Giá trị của \(\lim \left( {{u_n} + {v_n}} \right)\) bằng

A. 5

B. 6

C. -1

D. 1

Câu 2: \(\lim \frac{1}{{2n + 1}}\) bằng

A. 0

B. \(\frac{1}{2}\)

C. 1

D. \( + \infty .\)

Câu 3: \(\lim {\left( {\frac{1}{3}} \right)^n}\) bằng

A. 0

B. \(\frac{1}{3}\)

C. 1

D. \( + \infty .\)

Câu 4: \(\mathop {\lim }\limits_{x \to 2} \left( {{x^2} – 1} \right)\) bằng

A. 3

B. -1

C. 1

D. \( + \infty .\)

Câu 5: \(\mathop {\lim }\limits_{x \to  + \infty } \left( {2x + 3} \right)\) bằng

A. \( + \infty .\)

B. 2

C. 3

D. \( – \infty .\)

Câu 6: Cho hàm số \(y = f(x)\) có đồ thị (C) và đạo hàm \(f'(2) = 6.\) Hệ số góc của tiếp tuyến của (C) tại điểm \(M\left( {2;f\left( 2 \right)} \right)\) bằng

A. 6

B. 3

C. 2

D. 12

Câu 7: Đạo hàm của hàm số y = x² tại điểm x = 3 bằng

A. 6

B. 12

C. 3

D. 9

Câu 8: Đạo hàm của hàm số y = x² + x là

A. 2x + 1

B. 2x

C. 2x² + 1

D. 2x² + x

Câu 9: Đạo hàm của hàm số y = x³ – 2x là

A. 3x² – 2

B. 3x²

C. 3x³ – 2

D. 2x² – 2

Câu 10: Cho hai hàm số f(x) và g(x) có f’(1) = 2 và g’(1) = 3. Đạo hàm của hàm số f(x) + g(x)  tại điểm x = 1 bằng

A. 5

B. 6

C. 1

D. -1

Câu 11: Cho hai hàm số f(x) và g(x) có f’(1) = 3 và g’(1) = 1. Đạo hàm của hàm số f(x) – g(x) tại điểm x = 1 bằng

A. 2

B. 3

C. 4

D. -2

Câu 12: Cho hàm số f(x) có đạo hàm f’(x) = 2x + 4 với mọi \(x \in \mathbb{R}.\) Hàm số 2f(x) có đạo hàm là

A. 4x + 8

B. 4x + 4

C. x + 2

D. 2x + 6

Câu 13: Đạo hàm của hàm số \(y = \cos x\) là

A. –sin x

B. sin x

C. –cos x

D. cos x

Câu 14: \(\mathop {\lim }\limits_{x \to 0} \frac{{\sin x}}{x}\) bằng

A. 1

B. -1

C. 0

D. \( + \infty .\)

Câu 15: Đạo hàm của hàm số \(y = x + \sin x\) là

A. 1 + cos x

B. 1 – cos x

C. cos x

D. -cos x

Câu 16: Trong không gian, cho hình bình hành ABCD Vectơ \(\overrightarrow {AB}  + \overrightarrow {AD} \) bằng

A. \(\overrightarrow {AC} \)

B. \(\overrightarrow {BC} \)

C. \(\overrightarrow {BD} \)

D. \(\overrightarrow {CA} \)

Câu 17: Trong không gian, với \(\vec a,\vec b,\vec c\) là ba vectơ bất kỳ, mệnh đề nào dưới đây đúng ?

A. \(\vec a\left( {\vec b + \vec c} \right) = \vec a.\vec b + \vec a.\vec c.\)

B. \(\vec a\left( {\vec b – \vec c} \right) = \vec a.\vec b + \vec a.\vec c.\)

C. \(\vec a\left( {\vec b + \vec c} \right) = \vec a.\vec b – \vec a.\vec c.\)

D. \(\vec a\left( {\vec b + \vec c} \right) = \vec a.\vec b + \vec b.\vec c.\)

Câu 18: Trong không gian cho điểm A và mặt phẳng (P). Mệnh đề nào dưới đây đúng ?

A. Có đúng một đường thẳng đi qua A và vuông góc với (P).

B. Có đúng hai đường thẳng đi qua A và vuông góc với (P).

C. Có vô số đường thẳng đi qua A và vuông góc với (P).

D. Không tồn tại đường thẳng đi qua A và vuông góc với (P).

Câu 19: Hình lăng trụ đứng tam giác có bao nhiêu mặt là hình chữ nhật ?

A. 3

B. 5

C. 1

D. 2

 

Câu 20: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Khoảng cách từ A’ đến mặt phẳng (ABCD) bằng

A. 2a

B. a

C. 3a

D. \(\frac{a}{2}\)

Câu 21: Cho (u_n) là cấp số nhân với u₁= 3 và công bội \(q = \frac{1}{2}.\) Gọi S_n là tổng của n số hạng đầu tiên của cấp số nhân đã cho. Ta có lim S_n bằng

A. 6

B. \(\frac{1}{2}\)

C. 3

D. \(\frac{3}{2}\)

Câu 22: Giá trị thực của tham số m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 1\,\,\,{\rm{khi }}x \ge 2\\\,\,\,\,m\,\,\,\,\,\,\,{\rm{khi }}x < 2\end{array} \right.\) liên tục tại x = 2 bằng

A. 5

B. 3

C. 2

D. 1

Câu 23: Tiếp tuyến của đồ thị hàm số \(y = {x^3} – 2{x^2}\) tại điểm M(1; -1) có hệ số góc bằng

A. -1

B. 1

C. 7

D. 5

Câu 24: Đạo hàm của hàm số y = (2x + 1)² là

A. y’ = 8x + 4

B. y’ = 2x + 1

C. y’ = 4x + 2

D. y = 4x + 1

Câu 25: Đạo hàm của hàm số \(y = 3{x^2} + \sqrt x \) là

A. \(6x + \frac{1}{{2\sqrt x }}.\)

B. \(6x – \frac{1}{{2\sqrt x }}.\)

C. \(3x + \frac{1}{{2\sqrt x }}.\)

D. \(6x + \frac{1}{{\sqrt x }}.\)

Câu 26: Đạo hàm của hàm số \(y = \tan \left( {2x + 1} \right)\) là

A. \(\frac{2}{{{{\cos }^2}\left( {2x + 1} \right)}}.\)

B. \( – \frac{2}{{{{\cos }^2}\left( {2x + 1} \right)}}.\)

C. \(\frac{1}{{{{\cos }^2}\left( {2x + 1} \right)}}.\)

D. \(\frac{2}{{{{\sin }^2}\left( {2x + 1} \right)}}.\)

Câu 27: Đạo hàm của hàm số y = xsin x là

A. \(\sin x + x\cos x.\)

B. \(\sin x – x\cos x.\)

C. \(\sin x + \cos x.\)

D. \(\cos x + x\sin x.\)

Câu 28: Đạo hàm của hàm số \(y = \sin 2x\) là

A. \(2\cos 2x.\)

B. \( – 2\cos 2x.\)

C. \(\cos 2x.\)

D. \( – \cos 2x.\)

Câu 29: Đạo hàm cấp hai của hàm số \(y = {x^3} + 2x\) là

A. 6x

B. 6x + 2

C. 3x

D. 3x + 2

Câu 30: Cho hàm số \(f\left( x \right) = {\left( {x + 1} \right)^3}.\) Giá trị của \(f”\left( 1 \right)\) bằng

A. 12

B. 6

C. 24

D. 4

Câu 31: Trong không gian cho hai vectơ \(\vec u,\vec v\) tạo với nhau một góc \(60^\circ \), \(\left| {\vec u} \right| = 2\) và \(\left| {\vec v} \right| = 3.\) Tích vô hướng \(\vec u.\vec v\) bằng

A. 3

B. 6

C. 2

D. 3\(\sqrt 3 \)

Câu 32: Cho hình chóp S.ABCD có ABCD là hình chữ nhật và \(SA \bot (ABCD).\) Mệnh đề nào dưới đây đúng ?

A. \(AB \bot (SAD).\)

B. \(BC \bot (SAD).\)

C. \(AC \bot (SAD).\)

D. \(BD \bot (SAD).\)

Câu 33: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,\(SA \bot (ABCD)\) và SA = a. Góc giữa đường thẳng SB và mặt phẳng (ABCD) bằng

A. \(45^\circ .\)

B. \(90^\circ .\)

C. \(30^\circ .\)

D. \(60^\circ .\)

Câu 34: Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng đáy. Mặt phẳng (ABCD) vuông góc với mặt phẳng nào dưới đây ?

A. (SAC)

B. (SBD)

C. (SCD)

D. (SBC)

Câu 35: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(SA \bot (ABCD),\)AB = a và \(SB = \sqrt 2 a.\) Khoảng cách từ điểm S đến mặt phẳng (ABCD) bằng

A. a

B. \(\sqrt 2 \)a

C. 2a

D. \(\sqrt 3 \)a

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1: Cho hàm số \(f\left( x \right) = {x^3} + a{x^2} + bx + c\) với \(a,b,c \in \mathbb{R}.\) Hãy xác định các số a, b, c biết rằng \(f’\left( {\frac{1}{3}} \right) = 0\) và đồ thị của hàm số \(y = f\left( x \right)\) đi qua các điểm (-1; -3) và (1; -1).

Câu 2: Cho hình chóp đều S.ABCD có cạnh đáy bằng a, góc giữa cạnh bên và mặt phẳng đáy bằng \(60^\circ .\)Tính độ dài đường cao của hình chóp đã cho.

Câu 3: 

a) Giả sử hai hàm số \(y = f\left( x \right)\) và \(y = f\left( {x + 1} \right)\) đều liên tục trên đoạn [0; 2] và \(f\left( 0 \right) = f\left( 2 \right).\) Chứng minh phương trình \(f\left( x \right) – f\left( {x + 1} \right) = 0\) luôn có nghiệm thuộc đoạn [0; 1].

b) Cho hàm số \(y = \frac{{x + 2}}{{x + 1}}\) có đồ thị (C). Tìm điểm M thuộc (C) sao cho tiếp tuyến của (C) tại \(M\) tạo với hai trục tọa độ một tam giác vuông cân.

————-HẾT ———-

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 5

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 5)

I) TRẮC NGHIỆM: (7,0 điểm)

Câu 1: Cho hình hộp ABCD.A’B’C’D’ (hình vẽ minh hoạ).

Mệnh đề nào sau đây đúng ?

A.  \(\overrightarrow {AC’}  = \overrightarrow {AD}  + \overrightarrow {AC}  + \overrightarrow {AA’} .\)                            

B.  \(\overrightarrow {AC’}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA’} .\)

C.  \(\overrightarrow {AC’}  = \overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AA’} .\)                            

D.  \(\overrightarrow {AC’}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AC} .\)

Câu 2: Tìm đạo hàm của hàm số \(y = \tan x\,\)với \(x \ne \frac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}\).

A.  \(y’ =  – \frac{1}{{{{\sin }^2}x}}\).

B.  \(y’ = \frac{1}{{{{\sin }^2}x}}\).

C.  \(y’ =  – \frac{1}{{{{\cos }^2}x}}\).

D.  \(y’ = \frac{1}{{{{\cos }^2}x}}\).

Câu 3. Trong không gian, hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng

A. \[{0^0}\]               

B. \[{45^0}\]

C. \[{90^0}\]

D. \[{60^0}\]

Câu 4. Cho hàm số \[y = f\left( x \right)\] có đạo hàm tại điểm x₀. Chọn khẳng định ĐÚNG?

A. \[f’\left( {{x_0}} \right) = f\left( {{x_0}} \right)\]

B. \[f’\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) – f\left( {{x_0}} \right)}}{{x + {x_0}}}\]

C. \[f’\left( {{x_0}} \right) = \frac{{f\left( x \right) – f\left( {{x_0}} \right)}}{{x – {x_0}}}\]

D. \[f’\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) – f\left( {{x_0}} \right)}}{{x – {x_0}}}\]

Câu 5: Tính \(\mathop {\lim }\limits_{x \to  + \infty } {x^3}\) ta được kết quả là

A. 3.

B. \( + \infty \).

C. 0.

D. \( – \infty \).

Câu 6: Trong quy tắc tính đạo hàm bằng định nghĩa tại điểm x₀ của hàm số y = f(x) thì đại lượng \(\Delta y\) bằng

A. \(f({x_0} + \Delta x) + f({x_0})\).

B. \(f({x_0} – \Delta x) – f({x_0})\).

C. \(f({x_0} – \Delta x) + f({x_0})\).

D. \(f({x_0} + \Delta x) – f({x_0})\).

Câu 7: Cho đường thẳng \(\Delta \), mặt phẳng \((\alpha )\) và 2 đường thẳng a, b phân biệt thuộc \((\alpha )\). Điều kiện để đường thẳng \(\Delta \) vuông góc với mặt phẳng \((\alpha )\) là

A. \(\Delta  \bot a,\,\,\Delta  \bot b\) và a cắt b.

B. \(\Delta  \bot a,\,\,\Delta  \bot b\) và a // b.

C. \(\Delta  \bot a,\,\,\Delta  \bot b\) và \(\Delta \)// b.

D. \(\Delta  \bot a,\,\,\Delta  \bot b\) và \(\Delta \) cắt b.

Câu 8: Tính vi phân \(d\left( {{x^2} – 7x + 9} \right)\) ta được kết quả là

A. \(\left( {2x – 7} \right)dx\).

B. \(\left( {x – 7} \right)dx\).

C. \(\left( {x + 7} \right)dx\).

Câu 9. Tính \[\mathop {\lim }\limits_{} \frac{{{{2.3}^n} – 5}}{{{3^n} + 3}}.\]

A. \[ – \infty .\]

B. \[ + \infty .\]

C. 0.

D. 2.

Câu 10. Cho hàm số \[y = f(x) = \left\{ \begin{array}{l}\frac{{m\sqrt {x + 3}  – 2m\sqrt {2 – x} }}{{x – 1}}\quad khi\;x \ne 1\\\frac{{1009}}{2} – n\quad \quad \quad \,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\;x = 1\end{array} \right..\]Tìm điều kiện của tham số  m và n  để hàm số trên liên tục tại điểm  x = 1.

A. 5m + 4n = 2018

B. 4m – 5n = 2018

C. 4m + 5n = 2018

D. 5m – 4n = 2018

Câu 11. Cho hình chóp S.ABCD  có đáy ABCD là hình vuông cạnh a, \(SA \bot \left( {ABCD} \right)\) và SA = a.Tính khoảng cách từ điểm A đến mặt phẳng (SBC)

A. \(d\left( {A;\left( {SBC} \right)} \right) = a.\)    

B. \(d\left( {A;\left( {SBC} \right)} \right) = a\sqrt 2 .\)   

C. \(d\left( {A;\left( {SBC} \right)} \right) = \frac{{a\sqrt 3 }}{2}.\)

D. \(d\left( {A;\left( {SBC} \right)} \right) = \frac{{a\sqrt 2 }}{2}.\)

Câu 12: Cho hình chóp S.ABCD có đáy là hình thoi, cạnh bên SA vuông góc với mặt phẳng (ABCD) (như hình vẽ minh hoạ). Hãy chọn khẳng định đúng.

A.  \[BD \bot (SAC)\].

B.  \[CD \bot (SAD)\].   

C.  \[AC \bot (SBD)\]

D. \[BC \bot (SAB)\].

Câu 13: Cho lăng trụ ABC.A’B’C’ (hình vẽ minh hoạ). Vectơ \(\overrightarrow {A’A} \)  không phải là vectơ chỉ phương của đường thẳng nào sau đây ?

A.  \(BB’.\)

B.  \(AA’.\)                 

C.  \(BC.\)

D.  \[CC’.\]

Câu 14: Cho hàm số y = f(x) có đồ thị trên \(\mathbb{R}\) như hình vẽ bên. Hỏi hàm số bị gián đoạn tại điểm nào ?

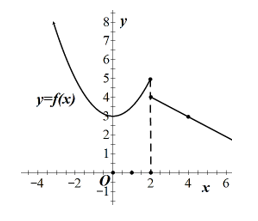
A. Tại điểm x₀  = -1.

B. Tại điểm x₀  = 2.

C. Tại điểm x₀  = -2.

D. Tại điểm x₀  = 1.

Câu 15. Cho hàm số  \(y = \frac{1}{{\sqrt {{x^4} + 1} }}\) . Mệnh đề nào dưới đây đúng ?

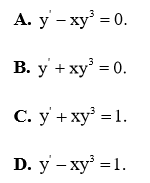
Câu 16: Cho một hàm số f(x). Khẳng định nào sau đây là đúng?

A. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a; b).

B. Nếu hàm số f(x) liên tục, đồng biến trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0  không có nghiệm trong khoảng (a; b).

C. Nếu f(x) liên tục trên đoạn [a; b], f(a).f(b) < 0 thì phương trình f(x) = 0 không có nghiệm trên khoảng (a; b).

D. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên tục trên khoảng (a; b).

Câu 17: Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?

A. \[{u_n} = \frac{{{n^3} – 2n + 3}}{{\sqrt {{n^4} + 4} }}\]

B. \[{u_n} = \sqrt {{n^2} + 2n}  – n\]

C. \[{u_n} = \frac{{3{n^4} – 1}}{{\sqrt {{n^6} + 2} }}\]

D. \[{u_n} = \frac{{2{n^3} – n}}{{{n^2} – 2}}\]

Câu 18: Biết \[\mathop {\lim }\limits_{x \to  + \infty } \frac{{2x}}{{a + x}} = 2\], khi đó a có giá trị là:

A. 1

B. Không tồn tại

C. \(\forall a \in \mathbb{R}\)

D. 0

Câu 19: Cho hàm số y = f(x) xác định trên tập số thực R thỏa mãn \[\mathop {\lim }\limits_{x \to 2} \frac{{f(x) – f(2)}}{{x – 2}} = 3\]. Kết quả nào sau đây là đúng?

A. f'(2) = 3

B. f'(3) = 2

C. f'(x) = 3

D. f'(x) = 2

Câu 20: Cho hàm số \[y = \sqrt {3x – 2} \]. Phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng \[y = \frac{3}{2}x + \frac{1}{2}\] là:

A. \[y = \frac{3}{2}x – \frac{1}{2}\]

B. \[y = \frac{3}{2}x – 1\]

C. \[y = \frac{3}{2}x + 1\]

D. \[y = \frac{3}{2}x – \frac{3}{2}\]

Câu 21: Đạo hàm của hàm số \(y = \sqrt {\sin 3x} \) là :

A. \(\frac{{3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

B. \(\frac{{\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

C. \(\frac{{ – \cos 3x}}{{2\sqrt {\sin 3x} }}.\)

D. \(\frac{{ – 3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

II.PHẦN TỰ LUẬN (3 điểm)

Câu 1 (1 điểm). Cho hàm số \(y =  – \frac{1}{3}{x^3} + 2m{x^2} – 3mx + 2\sqrt 2 \) , m là tham số.

a) Giải bất phương trình y’ > 0 khi m = 1.

b)Tìm điều kiện của tham số m để \(y’ \le 0,\forall x \in \mathbb{R}\) .

Câu 2(0,75 điểm). Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^3} + x\) tại điểm có hoành độ là 1.

Câu 3(1,25 điểm ). Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a. Biết SA = SC,  SB = SD, SO =\(\frac{{3a}}{4}\) và \(\widehat {ABC} = {60^0}\). Gọi I, J lần lượt là trung điểm của AB và BC.

a) Chứng minh \[SO \bot \left( {ABCD} \right),\,\,(SAC) \bot \left( {SBD} \right)\].

b) Tính khoảng cách giữa hai đường thẳng SO và IJ.

c) Tính góc giữa (SIJ) và mặt phẳng (SAC).

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 6

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 6)

I. Trắc nghiệm (7 điểm)

Câu 1: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC. Khẳng định nào sau đây đúng ?

A. \(SO \bot (ABCD)\)

B. \(BD \bot (SAC)\)

C. \(AC \bot (SBD)\)

D. \(AB \bot (SAD)\)

Câu 2: Dãy số nào sau đây có giới hạn bằng 0?

A. \(\frac{{\sqrt {2{n^2} – 1} }}{{5n + 3{n^2}}}\)

B. \(\frac{{1 – 2{n^2}}}{{5n + 3{n^2}}}\)

C. \({u_n} = \frac{{{n^2} – 2n}}{{5n + 3}}\)

D. \({u_n} = \frac{{{n^2} – 2}}{{\sqrt {1 + 3{n^2}} }}\)

Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \((SAB) \bot (ABC)\), SA = SB,  I là trung điểm AB. Khẳng định nào sau đây sai ?

A. Góc giữa SC và (ABC) là \(\widehat {SCI}\)

B. \(SI \bot (ABC)\)

C. \(AC \bot (SAB)\)

D. \(AB \bot (SAC)\)

Câu 4: Giới hạn\[\mathop {\lim }\limits_{x \to {1^ – }} \frac{{2x + 3}}{{1 – x}}\] là:

A. \[ – \infty \]              

B. 2

C. \[ + \infty \]

D. -2

Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Trong các tam giác sau tam giác nào không phải là tam giác vuông?

A. \[\Delta {\rm{SBC}}\]

B. \[\Delta {\rm{SAB}}\]

C. \[\Delta {\rm{SCD}}\]

D. \[\Delta {\rm{SBD}}\]

Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng ?

A. \((SCD) \bot (SAD)\)

B. \((SBC) \bot (SAC)\)

C. \((SDC) \bot (SAC)\)

D. \((SBD) \bot (SAC)\)

Câu 7: Khẳng định nào sau đây là đúng?

A. Hàm số \(f(x) = \frac{{x – 1}}{{x + 1}}\) gián đoạn tại x = 1

B. Hàm số \(f(x) = \frac{{x + 1}}{{{x^2} + 1}}\)liên tục trên \(\mathbb{R}\)

C. Hàm số \(f(x) = \frac{{{x^2} – 1}}{{x + 1}}\) liên tục trên\(\mathbb{R}\)

D. Hàm số \(f(x) = \frac{{x + 1}}{{x – 1}}\) liên tục trên (0; 2)

Câu 8: Một chất điểm chuyển động có phương trình \[s = {t^3} + 3t\] (t tính bằng giây, s tính bằng mét) Tính vận tốc của chất điểm tại thời điểm t₀ = 2 (giây) ?

A. 15 m/s

B. 7 m/s

C. 14 m/s

D. 12 m/s

Câu 9: Cho một hàm số f(x). Khẳng định nào sau đây là đúng?

A. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a; b).

B. Nếu hàm số f(x) liên tục, đồng biến trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0  không có nghiệm trong khoảng (a; b).

C. Nếu f(x) liên tục trên đoạn [a; b], f(a).f(b) < 0 thì phương trình f(x) = 0 không có nghiệm trên khoảng (a; b).

D. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên tục trên khoảng (a; b).

Câu 10: Hàm số\[y = \frac{{x + 6}}{{x + 9}}\]  có đạo hàm là:

A. \[\frac{3}{{{{\left( {x + 9} \right)}^2}}}\]

B. \[ – \frac{3}{{{{\left( {x + 9} \right)}^2}}}\]

C. \[\frac{{15}}{{{{\left( {x + 9} \right)}^2}}}\]

D. \[ – \frac{{15}}{{{{\left( {x + 9} \right)}^2}}}\]

Câu 11: \[\lim \left( {\sqrt {{n^2} + 3n}  – \sqrt {{n^2} + 2} } \right) = \frac{a}{b}\] (\(a,b \in \mathbb{Z}\) và \(\frac{a}{b}\) tối giản) thì tổng \[{a^2} + {b^2}\] là :

A. 10

B. 3

C. 13

D. 20

Câu 12: Cho hàm số \[f(x) = \frac{{a{x^2} + 4x + 3}}{{3x – 2a{x^2}}},(a \in R,a \ne 0)\]. Khi đó \[\mathop {\lim }\limits_{x \to  – \infty } f(x)\] bằng:

A. \(\frac{a}{3}\)         

B. \( – \frac{1}{2}\)

C. \( + \infty \)             

D. \( – \infty \)

Câu 13: Cho hình chóp S.ABC có \[SA \bot \left( {ABC} \right)\] và H là hình chiếu vuông góc của S lên BC. Khẳng định nào sau đây đúng?

A. \[AC \bot SH\]

B. \[BC \bot SC\]

C. \[AB \bot SH\]

D. \[BC \bot AH\]

Câu 14: . Hàm số\(y = {x^3} + 2{x^2} + \frac{{x + 4}}{2}\)   có đạo hàm  là:

A.\[y’ = 3{x^2} + 4x + \frac{1}{4}\]

B. \(y’ = 3{x^2} + 4x + 4\).

C.\(y’ = 3{x^2} + 4x + \frac{1}{2}\)

D. \(y’ = 3{x^2} + 4x + 2\)

Câu 15: Cho hàm số \[y = \sqrt {3x – 2} \]. Phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng \[y = \frac{3}{2}x + \frac{1}{2}\] là:

A. \[y = \frac{3}{2}x – \frac{1}{2}\]

B. \[y = \frac{3}{2}x – 1\]

C. \[y = \frac{3}{2}x + 1\]

D. \[y = \frac{3}{2}x – \frac{3}{2}\]

Câu 16: Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?

A. \[{u_n} = \frac{{{n^3} – 2n + 3}}{{\sqrt {{n^4} + 4} }}\]

B. \[{u_n} = \sqrt {{n^2} + 2n}  – n\]

C. \[{u_n} = \frac{{3{n^4} – 1}}{{\sqrt {{n^6} + 2} }}\]

D. \[{u_n} = \frac{{2{n^3} – n}}{{{n^2} – 2}}\]

Câu 17: Phương trình \({\mathop{\rm s}\nolimits} {\rm{inx}} = \mathop {\lim }\limits_{t \to 1} \frac{{2\sqrt {t + 3}  – 4}}{{t – 1}}\), có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\) là

A. \(\frac{\pi }{6}\)

B. vô nghiệm

C. \({30^0}\)               

D. \(\frac{1}{2}\)

Câu 18: Giới hạn \[\mathop {\lim }\limits_{x \to 0} \frac{{2 + \frac{3}{x}}}{{4 – \frac{1}{x}}}\] là:

A. \(\frac{1}{2}\)

B. 3

C. \(\frac{3}{4}\)

D. \( – 3\)

Câu 19: Biết \[\mathop {\lim }\limits_{x \to  + \infty } \frac{{2x}}{{a + x}} = 2\], khi đó a có giá trị là:

A. 1

B. Không tồn tại

C. \(\forall a \in \mathbb{R}\)

D. 0

Câu 20: Đạo hàm của hàm số \(y = \sqrt {\sin 3x} \) là :

A. \(\frac{{3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

B. \(\frac{{\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

C. \(\frac{{ – \cos 3x}}{{2\sqrt {\sin 3x} }}.\)

D. \(\frac{{ – 3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

Câu 21: Cho hàm số y = f(x) xác định trên tập số thực R thỏa mãn \[\mathop {\lim }\limits_{x \to 2} \frac{{f(x) – f(2)}}{{x – 2}} = 3\]. Kết quả nào sau đây là đúng?

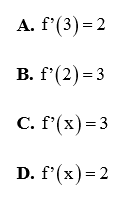
Câu 22: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, có cạnh SA =\[a\sqrt 2 \] và SA vuông góc với mp(ABCD). Tính góc giữa đường thẳng SC và mp(ABCD) là:

A. 45^o

 B. 30^o

C. 60^o

D. 90^o

Câu 23: Cho hình chóp tứ giác đều S.ABCD có đáy tâm O và M, N lần lượt là trung điểm của BC, CD. Khẳng định nào sau đây là sai ?

A. \((SBD) \bot (SAC)\)

B. Góc giữa (SBC) và (ABCD) là \(\widehat {SMO}\)

C. Góc giữa (SCD) và (ABCD) là \(\widehat {NSO}\)

D. \((SMO) \bot (SNO)\)

Câu 24: Cho hàm số \(y = f(x) = {\cos ^2}x + m\sin x\) có đồ thị (C). Giá trị  m để tiếp tuyến của (C) tại điểm có hoành độ \(x = \pi \) vuông góc với đường thẳng \(y =  – x\) là:

A. Không tồn tại.

B. 0.

C. 1.

D. -1.

Câu 25: Hàm số \(y = \cos x – \sin x + 2x\) có đạo hàm là:

A. \( – \sin x + \cos x + 2\)

B. \(\sin x – \cos x + 2\).

C. \( – \sin x – \cos x + 2\).

D. \( – \sin x – \cos x + 2x\).

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1 (1 điểm). Cho hàm số \(y =  – \frac{1}{3}{x^3} + 2m{x^2} – 3mx + 2\sqrt 2 \) , m là tham số.

a) Giải bất phương trình y’ < 0 khi m = 1.

b)Tìm điều kiện của tham số m để \(y’ \ge 0,\forall x \in \mathbb{R}\) .

Câu 2(0,75 điểm). Viết phương trình tiếp tuyến của đồ thị hàm số \(y = {x^4} + {x^2}\) tại điểm có hoành độ là 3.

Câu 3(1,25 điểm ). Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, cạnh a. Biết SA = SC,  SB = SD, SO =\(\frac{{3a}}{4}\) và \(\widehat {ABC} = {60^0}\). Gọi I, J lần lượt là trung điểm của AB và BC.

a) Chứng minh \[SO \bot \left( {ABCD} \right),\,\,(SAC) \bot \left( {SBD} \right)\].

b) Tính khoảng cách giữa hai đường thẳng SO và IJ.

c) Tính góc giữa (SIJ) và mặt phẳng (SAC).

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 7

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 7)

I. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1: Cho hình chóp S.ABCD, có đáy ABCD là hình vuông, \(SA \bot \left( {ABCD} \right)\). Khẳng định nào dưới đây là đúng?

A. \(\left( {SAB} \right) \bot \left( {ABCD} \right)\).                       

B. \(\left( {SAB} \right) \bot \left( {SAC} \right)\).

C. \(\left( {SAB} \right) \bot \left( {SCD} \right)\).

D. \(\left( {SAB} \right) \bot \left( {SBD} \right)\).

Câu 2: Tính \(\lim \frac{{10n}}{{2n – 3}}\)

A. 5.                          

B. \( – \frac{{10}}{3}\).

C. 0.                          

D. \( + \infty \).

Câu 3: Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Đẳng thức đúng là

A. \({\left( {\frac{u}{v}} \right)^\prime } = \frac{{u’v + uv’}}{{{v^2}}}\).

B. \((uv)’ = u’v – uv’\).

C. \((uv)’ = u’v + uv’\).

D. \[{\left( {\frac{u}{v}} \right)^\prime } = \frac{{u’v + uv’}}{v}\].

Câu 4: Trong không gian cho 3 điểm M, N, P phân biệt. Tính \(\overrightarrow {PM}  + \overrightarrow {MN} \).

A. \[\overrightarrow {PN} \].

B. \[\overrightarrow {NM} \].

C. \[\overrightarrow {MN} \].

D. \[\overrightarrow {NP} \].

Câu 5: Cho hàm số \(y = {x^7}\). Đẳng thức nào dưới đây đúng?

A. \(y” = 42{x^5}\).

B. \(y” = 14{x^6}\).

C. \(y” = 7{x^5}\).

D. \(y” = 7{x^6}\).

Câu 6: Trong hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào đúng?

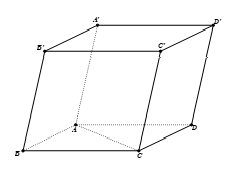
A. \[A’C’ \bot DD’\].

B. \[A’C’ \bot BB’\].

C. \[A’C’ \bot AC\].

D. \[A’C’ \bot BD\].

Câu 7: Tính \(\mathop {\lim }\limits_{x \to  + \infty } {x^3}\) ta được kết quả là

A. 3.

B. \( + \infty \).

C. 0.

D. \( – \infty \).

Câu 8: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 7 cm. Tính khoảng cách từ điểm B đến mặt phẳng (CDD’).

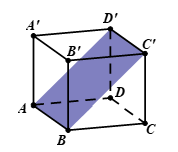
A. \(7\sqrt 3 \) cm.

B. 7 cm.

C. 14 cm.

D. \(7\sqrt 2 \) cm.

Câu 9: Đạo hàm của hàm số \(y = \cot x\) là

A. \(y’ = \cos x\).

B. \(y’ = \frac{1}{{{{\sin }^2}x}}\).

C. \(y’ =  – \frac{1}{{{{\sin }^2}x}}\).

D. \(y’ = \tan x\).

Câu 10: Đạo hàm của hàm số \(y = \sin x\) là

A. \(y’ = \cot x\).

B. \(y’ = \sin x\).

C. \(y’ = \tan x\).

D. \(y’ = \cos x\).

Câu 11: Cho đường thẳng \(\Delta \), mặt phẳng \((\alpha )\) và 2 đường thẳng a, b phân biệt thuộc \((\alpha )\). Điều kiện để đường thẳng \(\Delta \) vuông góc với mặt phẳng \((\alpha )\) là

A. \(\Delta  \bot a,\,\,\Delta  \bot b\) và a cắt b.

B. \(\Delta  \bot a,\,\,\Delta  \bot b\) và \(\Delta \) cắt b.

C. \(\Delta  \bot a,\,\,\Delta  \bot b\) và a // b.

D. \(\Delta  \bot a,\,\,\Delta  \bot b\) và \(\Delta \)// b.

Câu 12: Trong quy tắc tính đạo hàm bằng định nghĩa tại điểm x₀ của hàm số y = f(x) thì đại lượng \(\Delta y\) bằng

A. \(f({x_0} + \Delta x) + f({x_0})\).

B. \(f({x_0} – \Delta x) – f({x_0})\).

C. \(f({x_0} – \Delta x) + f({x_0})\).

D. \(f({x_0} + \Delta x) – f({x_0})\).

Câu 13: Cho hình hộp ABCD.MNPQ. Phép chiếu song song lên mặt phẳng (MNPQ) theo phương BM biến điểm C thành điểm

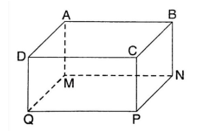
A. N.                          

B. Q.

C. M.                         

D. P.

Câu 14: Tính vi phân \(d\left( {{x^2} – 7x + 9} \right)\) ta được kết quả là

A. \(\left( {2x – 7} \right)dx\).

B. \(\left( {x – 7} \right)dx\).

C. \(\left( {x + 7} \right)dx\).

D. \(\left( {2x + 7} \right)dx\).

Câu 15: Hàm số nào liệt kê dưới đây liên tục trên \(\mathbb{R}\)?

A. \(y = \frac{1}{{{x^2} + 3}}\) .

B. \(y = \frac{1}{{{x^2} – 3}}\) .

C. \(y = \frac{4}{{{x^2}}}\).

D. \(y = \frac{3}{{{x^2}}}\).

Câu 16: Tính đạo hàm của hàm số \(f(x) = {x^{2020}}\) .

A. \(f'(x) = 2020{x^{2021}}\).

B. \(f'(x) = 2019{x^{2020}}\).

C. \(f'(x) = 2020x\).

D. \(f'(x) = 2020{x^{2019}}\).

Câu 17:  Tính giới hạn \(I = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} – 5x + 6}}{{x – 2}}\).

A. I = 1.

B. I = 5.

C. I = -1.

D. I = 0.

Câu 18: Đạo hàm của hàm số y = c (c là hằng số) là

A. y’ = y.

B. y’ = c.

C. y’ = 1.

D. y’ = 0.

Câu 19: Phương trình tiếp tuyến của đồ thị (C) của hàm số y = f(x) tại điểm \({M_0}\left( {{x_0};{y_0}} \right)\) là

A. \(y = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right) + {y_0}\).

B. \(y + {y_0} = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right)\).

C. \(y + {y_0} = f’\left( {{x_0}} \right)\left( {x + {x_0}} \right)\).

D. \(y = f’\left( {{x_0}} \right)\left( {x – {x_0}} \right) – {y_0}\).

Câu 20:  Giả sử u = u(x). Khi đó đẳng thức nào sau đây đúng?

A. \({\left( {{u^n}} \right)^\prime } = {u^{n – 1}}.u’\,\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

B. \({\left( {{u^n}} \right)^\prime } = n.u’\,\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

C. \({\left( {{u^n}} \right)^\prime } = n.{u^{n – 1}}\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

D. \({\left( {{u^n}} \right)^\prime } = n.{u^{n – 1}}.u’\,\,\,\,\,\,\left( {n \in {\mathbb{N}^*}} \right)\).

Câu 21:  Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\). Khi đó đẳng thức nào dưới đây là sai?

A. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\).

B. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right)g\left( x \right)} \right] = L + M\).

C. \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{L}{M},\,\,\,\left( {M \ne 0} \right)\).

D. \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) – g\left( x \right)} \right] = L – M\).

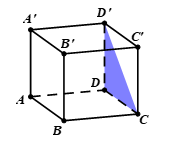
Câu 22: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 8 cm. Tính khoảng cách giữa đường thẳng A’B’ đến mặt phẳng (ABC’D’).

A. 4 cm.

B. \(4\sqrt 2 \) cm.

C. \(8\sqrt 2 \) cm.

D. 8 cm.

Câu 23: Cho một vật chuyển động theo phương trình \(S = {t^3} + m{t^2} + 10t + {m^2}\), trong đó t được tính bằng giây, S được tính bằng mét và m là tham số thực. Biết tại thời điểm t = 4s vận tốc của vật bị triệt tiêu. Gọi a là gia tốc của vật tại thời điểm t = 5s. Chọn khẳng định đúng trong các khẳng định sau

A. \(a \in \left( {30;40} \right)\).

B. \(a \in \left( {20;30} \right)\).

C. \(a \in \left( {0;10} \right)\).

D. \(a \in \left( {10;20} \right)\).

Câu 24:  Đạo hàm của hàm số \(y = \sin 3x\) là

A. \(y’ = \sin 3x\).

B. \(y’ = 3\cos 3x\).

C. \(y’ = \cos 3x\).

D. \(y’ = 3\sin 3x\).

Câu 25: Cho hàm số y = f(x) có đồ thị trên \(\mathbb{R}\) như hình vẽ bên. Hỏi hàm số bị gián đoạn tại điểm nào ?

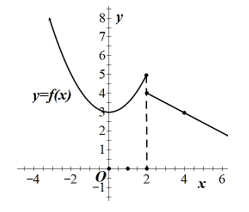
A. Tại điểm x₀  = -1.

B. Tại điểm x₀  = 1.

C. Tại điểm x₀  = 2.

D. Tại điểm x₀  = -2.

Câu 26: Một vật chuyển động theo phương trình \(S = {t^2} + 9t + 13\), trong đó t được tính bằng giây và S được tính bằng mét. Tính vận tốc tức thời của chuyển động khi t = 8 giây.

A. 23 (m/s) .

B. 25 (m/s).

C. 24 (m/s).

D. 149 (m/s) .

Câu 27: Biết \(f(x),g(x)\) là các hàm số liên tục trên \(\mathbb{R}\). Tính đạo hàm của hàm số \(h(x) = f(\pi  – {x^2}) + g\left( {\frac{1}{{{x^3}}}} \right) + {a^4}\)  (với \(x \ne 0,a\) là hằng số) .

A. \(h'(x) = 2xf’\left( {\pi  – {x^2}} \right) + \frac{3}{{{x^4}}}g’\left( {\frac{1}{{{x^3}}}} \right)\) .

B. \(h'(x) =  – 2xf’\left( {\pi  – {x^2}} \right) – \frac{3}{{{x^4}}}g’\left( {\frac{1}{{{x^3}}}} \right) + 4{a^3}\) .

C. \(h'(x) =  – 2xf’\left( {\pi  – {x^2}} \right) – \frac{3}{{{x^4}}}g’\left( {\frac{1}{{{x^3}}}} \right)\) .

D. \(h'(x) =  – 2xf’\left( {\pi  – {x^2}} \right) – \frac{1}{{{x^6}}}g’\left( {\frac{1}{{{x^3}}}} \right)\) .

Câu 28: Phương trình tiếp tuyến \(\Delta \) tại điểm M(-2; 5) thuộc đồ thị (C) của hàm số \(y = \frac{{3x + 1}}{{x + 1}}\) là

A. \(\Delta :y =  – x + 6\).

B. \(\Delta :y =  – x\).

C. \(\Delta :y = 2x + 9\).

D. \(\Delta :y = 5x + 3\).

Câu 29: Biết rằng \(\lim \frac{{{1^2} + {2^2} + {3^2} + … + {n^2}}}{{7 – 2{n^3}}} = \frac{p}{q}\) (với q > 0 và \(\frac{p}{q}\) là số hữu tỉ tối giản). Tính p.q.

A. -10.

B. -6.

C. -3 .

D. -100 .

Câu 30: Cho hàm số \(f(x) = \frac{{4x + 50}}{{{x^2} – 25}}\). Tính \({f^{(2022)}}\left( 4 \right)\) ta được kết quả là

A. \( – 7.2022! – \frac{{4.2022!}}{{{9^{2023}}}}\).

B. \({\left( { – \frac{{22}}{3}} \right)^{2022}}\) .

C. \( – 7.2022! + \frac{{3.2022!}}{{{9^{2023}}}}\) .

D. \( – 7.2022! – \frac{{3.2022!}}{{{9^{2023}}}}\).

Câu 31: Giới hạn \(\mathop {\lim }\limits_{x \to 5} \frac{{\sqrt {x + 11}  – \sqrt[3]{{x + 59}}}}{{x – 5}} = \frac{m}{n}\) (\(\frac{m}{n}\) là phân số tối giản). Tính 2m + n bằng

A. 59.

B. 57.

C. 60.

D. 58.

Câu 32: Đạo hàm của hàm số \(y = {x^3} + 5{x^2} – 6x + 12\) là

A. \(y’ = {x^2} + 2x + 4\).

B. \(y’ = 7{x^2} + 2x – 4\).

C. \(y’ = 3{x^2} + 10x – 6\).

D. \(y’ = {x^3} + 3{x^2} – 6x\).

Câu 33: Đạo hàm cấp hai của hàm số \(y = \cos 5x\) là

A. \(y” =  – \sin 5x\).

B. \(y” =  – 5\sin 5x\).

C. \(y” =  – 25\cos 5x\).

D. \(y” = 10\cos 5x\).

Câu 34: Tính đạo hàm của hàm số \(y = \sqrt {1 – 3{x^2}} \).

A. \(y’ = \frac{{ – 6x}}{{\sqrt {1 – 3{x^2}} }}\).

B. \(y’ = \frac{{ – 3x}}{{2\sqrt {1 – 3{x^2}} }}\) .

C. \(y’ = \frac{1}{{2\sqrt {1 – 3{x^2}} }}\).

D. \(y’ = \frac{{ – 3x}}{{\sqrt {1 – 3{x^2}} }}\) .

Câu 35: Tính \(\lim \left( {4n – 2{n^5} + 7{n^2}} \right)\)

A. \( + \infty \).

B. 4.

C. 7.

D. \( – \infty \) .

II. Tự luận (3 điểm)

Câu 1 (1 điểm): Cho hàm số \(y = \frac{{x + 1}}{{x – 2}}\) có đồ thị là (H). Viết phương trình tiếp tuyến của (H) tại điểm \({M_0}\left( {1; – 2} \right)\).

Câu 3 (2 điểm): Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác đều, hình chiếu vuông góc của S lên mặt phẳng ABCD trùng với trung điểm H của cạnh AB.

a) Chứng minh rằng: \(BC \bot \left( {SAB} \right)\)

b) Gọi K là trung điểm của cạnh BC, tính khoảng cách giữa hai đường thẳng HK và SC. Xác định đoạn vuông góc chung của của hai đường thẳng HK và SC.

Đề thi Toán lớp 11 học kì 2 năm 2022 có ma trận (8 đề) – Đề 8

Phòng Giáo dục và Đào tạo …..

Đề thi Học kì 2 – Năm học 2022 – 2023

Môn: Toán lớp 11

Thời gian làm bài: 90 phút

(Đề 8)

I. Trắc nghiệm (7 điểm)

Câu 1: \[\lim \left( {\sqrt {{n^2} + 3n}  – \sqrt {{n^2} + 2} } \right) = \frac{a}{b}\] (\(a,b \in \mathbb{Z}\) và \(\frac{a}{b}\) tối giản) thì tổng \[{a^2} + {b^2}\] là :

A. 10

B. 3

C. 13

D. 20

Câu 2: Dãy số nào sau đây có giới hạn bằng 0?

A. \(\frac{{\sqrt {2{n^2} – 1} }}{{5n + 3{n^2}}}\)

B. \(\frac{{1 – 2{n^2}}}{{5n + 3{n^2}}}\)

C. \({u_n} = \frac{{{n^2} – 2n}}{{5n + 3}}\)

D. \({u_n} = \frac{{{n^2} – 2}}{{\sqrt {1 + 3{n^2}} }}\)

Câu 3: Giới hạn\[\mathop {\lim }\limits_{x \to {1^ – }} \frac{{2x + 3}}{{1 – x}}\] là:

A. \[ – \infty \]              

B. 2

C. \[ + \infty \]

D. -2

Câu 4: Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O và SA = SC. Khẳng định nào sau đây đúng ?

A. \(SO \bot (ABCD)\)

B. \(BD \bot (SAC)\)

C. \(AC \bot (SBD)\)

D. \(AB \bot (SAD)\)

Câu 5: Khẳng định nào sau đây là đúng?

A. Hàm số \(f(x) = \frac{{x – 1}}{{x + 1}}\) gián đoạn tại x = 1

B. Hàm số \(f(x) = \frac{{x + 1}}{{{x^2} + 1}}\)liên tục trên \(\mathbb{R}\)

C. Hàm số \(f(x) = \frac{{{x^2} – 1}}{{x + 1}}\) liên tục trên\(\mathbb{R}\)

D. Hàm số \(f(x) = \frac{{x + 1}}{{x – 1}}\) liên tục trên (0; 2)

Câu 6: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy. Khẳng định nào sau đây đúng ?

A. \((SCD) \bot (SAD)\)

B. \((SBC) \bot (SAC)\)

C. \((SDC) \bot (SAC)\)

D. \((SBD) \bot (SAC)\)

Câu 7: Một chất điểm chuyển động có phương trình \[s = {t^3} + 3t\] (t tính bằng giây, s tính bằng mét) Tính vận tốc của chất điểm tại thời điểm t₀ = 2 (giây) ?

A. 15 m/s

B. 7 m/s

C. 14 m/s

D. 12 m/s

Câu 8: Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, \((SAB) \bot (ABC)\), SA = SB,  I là trung điểm AB. Khẳng định nào sau đây sai ?

A. Góc giữa SC và (ABC) là \(\widehat {SCI}\)

B. \(SI \bot (ABC)\)

C. \(AC \bot (SAB)\)

D. \(AB \bot (SAC)\)

Câu 9: Cho một hàm số f(x). Khẳng định nào sau đây là đúng?

A. Nếu f(a).f(b) < 0 thì phương trình f(x) = 0 có ít nhất một nghiệm trong khoảng (a; b).

B. Nếu hàm số f(x) liên tục, đồng biến trên đoạn [a; b] và f(a).f(b) > 0 thì phương trình f(x) = 0  không có nghiệm trong khoảng (a; b).

C. Nếu f(x) liên tục trên đoạn [a; b], f(a).f(b) < 0 thì phương trình f(x) = 0 không có nghiệm trên khoảng (a; b).

D. Nếu phương trình f(x) = 0 có nghiệm trong khoảng (a; b) thì hàm số f(x) phải liên tục trên khoảng (a; b).

Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(SA \bot \left( {ABCD} \right)\). Trong các tam giác sau tam giác nào không phải là tam giác vuông?

A. \[\Delta {\rm{SBC}}\]

B. \[\Delta {\rm{SAB}}\]

C. \[\Delta {\rm{SCD}}\]

D. \[\Delta {\rm{SBD}}\]

Câu 11: Hàm số\[y = \frac{{x + 6}}{{x + 9}}\]  có đạo hàm là:

A. \[\frac{3}{{{{\left( {x + 9} \right)}^2}}}\]

B. \[ – \frac{3}{{{{\left( {x + 9} \right)}^2}}}\]

C. \[\frac{{15}}{{{{\left( {x + 9} \right)}^2}}}\]

D. \[ – \frac{{15}}{{{{\left( {x + 9} \right)}^2}}}\]

Câu 12: Cho hình chóp S.ABC có \[SA \bot \left( {ABC} \right)\] và H là hình chiếu vuông góc của S lên BC. Khẳng định nào sau đây đúng?

A. \[AC \bot SH\]

B. \[BC \bot SC\]

C. \[AB \bot SH\]

D. \[BC \bot AH\]

Câu 13: Cho hàm số \[f(x) = \frac{{a{x^2} + 4x + 3}}{{3x – 2a{x^2}}},(a \in R,a \ne 0)\]. Khi đó \[\mathop {\lim }\limits_{x \to  – \infty } f(x)\] bằng:

A. \(\frac{a}{3}\)         

B. \( – \frac{1}{2}\)

C. \( + \infty \)             

D. \( – \infty \)

Câu 14: . Hàm số\(y = {x^3} + 2{x^2} + \frac{{x + 4}}{2}\)   có đạo hàm  là:

A.\[y’ = 3{x^2} + 4x + \frac{1}{4}\]

B.\(y’ = 3{x^2} + 4x + \frac{1}{2}\)

C. \(y’ = 3{x^2} + 4x + 4\).

D. \(y’ = 3{x^2} + 4x + 2\)

Câu 15: Cho hàm số \[y = \sqrt {3x – 2} \]. Phương trình tiếp tuyến của đồ thị hàm số biết tiếp tuyến song song với đường thẳng \[y = \frac{3}{2}x + \frac{1}{2}\] là:

A. \[y = \frac{3}{2}x – \frac{3}{2}\]

B. \[y = \frac{3}{2}x – 1\]

C. \[y = \frac{3}{2}x + 1\]

D. \[y = \frac{3}{2}x – \frac{1}{2}\]

Câu 16: Trong các dãy số sau, dãy số nào có giới hạn hữu hạn?

A. \[{u_n} = \frac{{{n^3} – 2n + 3}}{{\sqrt {{n^4} + 4} }}\]

B. \[{u_n} = \sqrt {{n^2} + 2n}  – n\]

C. \[{u_n} = \frac{{3{n^4} – 1}}{{\sqrt {{n^6} + 2} }}\]

D. \[{u_n} = \frac{{2{n^3} – n}}{{{n^2} – 2}}\]

Câu 17: Giới hạn \[\mathop {\lim }\limits_{x \to 0} \frac{{2 + \frac{3}{x}}}{{4 – \frac{1}{x}}}\] là:

A. \(\frac{1}{2}\)

B. 3

C. \(\frac{3}{4}\)

D. \( – 3\)

Câu 18: Phương trình \({\mathop{\rm s}\nolimits} {\rm{inx}} = \mathop {\lim }\limits_{t \to 1} \frac{{2\sqrt {t + 3}  – 4}}{{t – 1}}\), có nghiệm \(x \in \left( {0;\frac{\pi }{2}} \right)\) là

A. \(\frac{\pi }{6}\)

B. vô nghiệm

C. \({30^0}\)               

D. \(\frac{1}{2}\)

Câu 19: Biết \[\mathop {\lim }\limits_{x \to  + \infty } \frac{{2x}}{{a + x}} = 2\], khi đó a có giá trị là:

A. 1

B. Không tồn tại

C. \(\forall a \in \mathbb{R}\)

D. 0

Câu 20: Cho hàm số y = f(x) xác định trên tập số thực R thỏa mãn \[\mathop {\lim }\limits_{x \to 2} \frac{{f(x) – f(2)}}{{x – 2}} = 3\]. Kết quả nào sau đây là đúng?

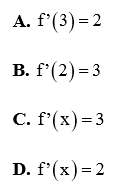
Câu 21: Đạo hàm của hàm số \(y = \sqrt {\sin 3x} \) là :

A. \(\frac{{3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

B. \(\frac{{\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

C. \(\frac{{ – \cos 3x}}{{2\sqrt {\sin 3x} }}.\)

D. \(\frac{{ – 3\cos 3x}}{{2\sqrt {\sin 3x} }}.\)

Câu 22: Cho hình chóp tứ giác đều S.ABCD có đáy tâm O và M, N lần lượt là trung điểm của BC, CD. Khẳng định nào sau đây là sai ?

A. \((SBD) \bot (SAC)\)

B. Góc giữa (SBC) và (ABCD) là \(\widehat {SMO}\)

C. Góc giữa (SCD) và (ABCD) là \(\widehat {NSO}\)

D. \((SMO) \bot (SNO)\)

Câu 23: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, có cạnh SA =\[a\sqrt 2 \] và SA vuông góc với mp(ABCD). Tính góc giữa đường thẳng SC và mp(ABCD) là:

A. 45^o

 B. 30^o

C. 60^o

D. 90^o

Câu 24: Cho hàm số \(y = f(x) = {\cos ^2}x + m\sin x\) có đồ thị (C). Giá trị  m để tiếp tuyến của (C) tại điểm có hoành độ \(x = \pi \) vuông góc với đường thẳng \(y =  – x\) là:

A. Không tồn tại.

B. 0.

C. 1.

D. -1.

Câu 25: Hàm số \(y = \cos x – \sin x + 2x\) có đạo hàm là:

A. \( – \sin x + \cos x + 2\)

B. \(\sin x – \cos x + 2\).

C. \( – \sin x – \cos x + 2\).

D. \( – \sin x – \cos x + 2x\).

II. Tự luận (3 điểm)

Câu 1 (1 điểm): Tính đạo hàm của các hàm số sau

a) \(y = 3{{\rm{x}}^2} + \sqrt {x + 1} \)

b) \(y = {\sin ^3}x + \cot {\rm{5x}}\)

Câu 2 (0,5 điểm): Cho hàm số \(y = \frac{{x + 1}}{{x – 2}}\) có đồ thị là (H). Viết phương trình tiếp tuyến của (H) tại điểm \({M_0}\left( {1; – 2} \right)\).

Câu 3 (1,5 điểm). Cho hình chóp S.ABC có đáy là tam giác đều cạnh 4a. Biết SB vuông góc với mặt đáy và P là trung điểm của cạnh AC.

a) Chứng minh rằng \(AC \bot (SBP)\)

b) Gọi G là trọng tâm của tam giác ABC. Tính khoảng cách từ điểm G đến mặt phẳng (SAC) biết góc tạo bởi (SAC) và mặt phẳng (ABC) bằng \({60^0}\).