Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung:
1. Vecto trong không gian
2. Hai đưởng thẳng vuông góc
3. Đưởng thẳng vuông góc với mặt phẳng
4. Hai mặt phẳng vuông góc
5. Khoảng cách
Chuyên đề vectơ trong không gian, quan hệ vuông góc – bản 2
Chương 3: Quan hệ vuông góc
Bài 1. Vec – to trong không gian
(A) Tóm tắt lý thuyết
1) Các định nghĩa
(1) Véc-tơ là một đoạn thẳng có hướng (có phân biệt điểm đầu và điểm cuối).
(2) Véc-tơ – không là véc-tơ có điểm đầu và điểm cuối trùng nhau. Ký hiệu \(\vec 0\).
(3) Ký hiệu véc-tơ: \(\overrightarrow {AB} \) (điểm đầu là A, điểm cuối là B ) hay \(\vec a,\vec b,\vec x,\vec y, \ldots \)
(4) Độ dài của véc-tơ là khoảng cách giữa điểm đầu và điểm cuối của véc-tơ đó.
Độ dài của \(\overrightarrow {AB} \) ký hiệu là \(|\overrightarrow {AB} |\), độ dài của \(\vec a\) ký hiệu là \(|\vec a|\).
(5) Giá của véc-tơ là đường thẳng đi qua điểm đầu và điểm cuối của véc-tơ đó.
(6) Hai véc-tơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
(7) Hai véc-tơ cùng phương thì cùng hướng hoặc ngược hướng.
(8) Hai véc-tơ bằng nhau là hai véc-tơ cùng hướng và có cùng độ dài.
Tức là \(\vec a = \vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\vec a,\vec b{\rm{ c\`u ng huong }}}\\{|\vec a| = |\vec b|}\end{array}} \right.\)
(9) Hai véc-tơ đối nhau là hai véc-tơ ngược hướng nhưng vẫn có cùng độ dài.
(10) Các phép toán cộng, trừ, nhân véc-tơ với một số được định nghĩa tương tự trong mặt phẳng.
2. Các quy tắc tính toán vớ véc-to
(1) Quy tắc ba điểm (với phép cộng): \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
(2) Quy tắc ba điểm (với phép trừ): \(\overrightarrow {OB} – \overrightarrow {OA} = \overrightarrow {AB} \).
(3) Quy tắc ba điểm (mở rộng): \(\overrightarrow {A{X_1}} + \overrightarrow {{X_1}{X_2}} + \overrightarrow {{X_2}{X_3}} + \cdots + \overrightarrow {{X_{n – 1}}{X_n}} + \overrightarrow {{X_n}B} = \overrightarrow {AB} \).
(4) Quy tắc hình bình hành:
(a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {2AE} \)
trong đó ABCD là hình bình hành và E là trung điểm của BD.
5) Quy tắc hình hộp
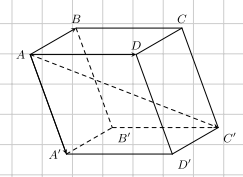
\(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A^\prime }} = \overrightarrow {A{C^\prime }} \)
Trong đó ABCD.A’B’C’D’ là hình hộp.
3. Một số hệ thức véc-to trọng tâm, cần nhớ
(1) I là trung điểm của đoạn thẳng \(AB \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} = \vec 0 \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} = 2\overrightarrow {OI} \) (với O là một điểm bất kỳ).
(2) G là trọng tâm của tam giác \(ABC \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0 \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} \) \( \Leftrightarrow \overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} \) (với O là một điểm bất kỳ, M là trung điểm cạnh BC.
(3) G là trọng tâm của tứ diện \(ABCD \Leftrightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\) \( \Leftrightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = 4\overrightarrow {OG} \Leftrightarrow \overrightarrow {AG} = \frac{3}{4}\overrightarrow {A{A^\prime }} \)
(với điểm O bất kỳ, \({A^\prime }\) là trọng tâm của )
\( \Leftrightarrow \overrightarrow {GM} + \overrightarrow {GN} = \vec 0\) (với M, N là trung điểm 1 cặ cạnh đối diện)
(4) \(\vec a\) và \(\vec b \ne \vec 0\) cùng phương \( \Leftrightarrow \exists k \in \mathbb{R}:\vec a = k \cdot \vec b\).
(5) \(\vec a\) và \(\vec b \ne \vec 0\) cùng hướng \( \Leftrightarrow \exists k \in {\mathbb{R}^ + }:\vec a = k \cdot \vec b\).
(6) \(\vec a\) và \(\vec b \ne \vec 0\) ngược hướng \( \Leftrightarrow \exists k \in {\mathbb{R}^ – }:\vec a = k \cdot \vec b\).
(7) Ba điểm A, B, C thẳng hàng \( \Leftrightarrow \exists k \in \mathbb{R}:\overrightarrow {AB} = k \cdot \overrightarrow {AC} \).
4. Điều kiện đồng phẳng của ba véc-to
Định nghĩa 1. Trong không gian, ba véc-tơ được gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng nào đó.
Hệ quả 1. Nếu có một mặ̣t phẳng chứa véc-tơ này đồng thời song song với giá của hai véc-tơ kia thì ba véc-tơ đó đồng phẳng.
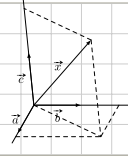
Định lí 1. (Điều kiện để ba véc-tơ đồng phẳng) Trong không gian cho hai véc-to a và \(\vec b\) không cùng phương và véc-tơ \(\vec c\). Khi đó \(\vec a,\vec b\) và \(\vec c\) đồng phẳng khi và chỉ khi tồn tại cặp số (m; n) sao cho \(\vec c = m\vec a + n\vec b\) (cặp số (m,n) nêu trên là duy nhất).
Bốn điểm phân biệt A, B, C, D đồng phẳng \( \Leftrightarrow \overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) đồng phẳng \( \Leftrightarrow \overrightarrow {AB} = m\overrightarrow {AC} + n\overrightarrow {AD} \).
(5) Phân tích một véc-to theo ba véc-to không đồng phẩng
Định lí 2 .
Cho ba vecto \(\vec a,\overrightarrow b \)và \(\vec c\) không đồng phẳng. Với mọi véc-tơ \(\vec x\), ta đều tìm dược duy nhất một bộ số (m,n,p) sao cho \(\vec x = m\vec a + n\vec b + p\vec c\).
6. Tích vô hướng của hai véc-to
Định nghĩa 2 .
(1) Nếu \(\overrightarrow a \ne \vec 0\)và \(\vec b \ne \vec 0\) thì \(\vec a \cdot \vec b = |\vec a| \cdot |\vec b| \cdot \cos (\vec a,\vec b)\)
(2) Nếu \(\vec a = \vec 0\) hoặc \(\vec b = \vec 0\) thì \(\vec a \cdot \vec b = 0\).
(3) Bình phương vô hướng của một véc-tơ: \({\vec a^2} = |\vec a{|^2}\).
Một số ứng dụng của tích vô hướng
(1) Nếu \(\vec a \ne \vec 0\) và \(\vec b \ne \vec 0\) ta có \(\vec a \bot \vec b \Leftrightarrow \vec a \cdot \vec b = 0\).
(2) Công thúc tính cô-sin của góc hợp bởi hai véc-to khác \(\vec 0:\cos (\vec a,\vec b) = \frac{{\vec a \cdot \vec b}}{{|\vec a| \cdot |\vec b|}}\).
(3) Công thức tính độ dài của mọt toan thẳng: \(AB = |\overrightarrow {AB} | = \sqrt {\overrightarrow {A{B^2}} } \).
B Các dạng toán
Dạng 1. Xác định véc-tơ và các khái niệm có liên quan
Phưong pháp giải:
– Dưa vào định nghĩa của các khái niệm liên quan đến véc-to (xem mục 1)
– Dựa vào tính chất hình học của các hình hình học cụ thể.
Ví dụ 1. Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Hãy xác định các véc-tơ (khác \(\vec 0\) ) có điểm đầu, điểm cuối là các đỉnh của hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) và
a) cùng phương với \(\overrightarrow {AB} \);
b) cùng phương \(\overrightarrow {A{A^\prime }} \).
Lời giải.
a) Các véc-tơ có điểm đầu, điểm cuối là các đỉnh của hình hộp cùng phương với \(\overrightarrow {AB} \) là
\(\overrightarrow {BA} ;\overrightarrow {CD} ;\overrightarrow {DC} ;\overrightarrow {{A^\prime }{B^\prime }} ;\overrightarrow {{B^\prime }{A^\prime }} ;\overrightarrow {{C^\prime }{D^\prime }} ;\overrightarrow {{D^\prime }{C^\prime }} \)
b. Các véc-tơ có điểm đầu, điểm cuối là các đỉnh của hình hộp cùng phương với \(\overrightarrow {AA’} \) là
\(\overrightarrow {A{A^\prime }} ;\overrightarrow {{A^\prime }A} ;\overrightarrow {B{B^\prime }} ;\overrightarrow {{B^\prime }B} ;\overrightarrow {C{C^\prime }} ;\overrightarrow {{C^\prime }C} ;\overrightarrow {D{D^\prime }} ;\overrightarrow {{D^\prime }D} \)
Ví dụ 2. Cho hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }D_ \to ^\prime \) Gọi \(O,{O^\prime }\) lần lượt là các giao điểm của hai đường chéo của hai đáy. Hãy xác định các véc-tơ (khác \(\vec 0\) ) có điểm đầu, điểm cuối là các đỉnh của hình lập phương \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) sao cho
a) bằng \(\overrightarrow {O{O^\prime }} \).
b) bằng \(\overrightarrow {AO} \).
Lời giải.
a) Ta có \(\overrightarrow {O{O^\prime }} = \overrightarrow {A{A^\prime }} = \overrightarrow {B{B^\prime }} = \overrightarrow {C{C^\prime }} = \overrightarrow {D{D^\prime }} \).
b) Ta có Các véc-tơ thỏa mãn là: \(\overrightarrow {AO} = \overrightarrow {{A^\prime }{O^\prime }} = \overrightarrow {OC} = \overrightarrow {{O^\prime }{C^\prime }} \).
Dạng 2. Chứng minh đẳng thức véc-tơ
Phương pháp giải:
Để chứng minh đẳng thức véc-tơ ta thường sử dụng:
– Qui tắc cộng, qui tắc trừ ba điểm, qui tăc hình bình hành, quy tăc hình hộp.
– Tính chất trung điểm, trọng tâm tam giác, tích một số với một véc-tơ… Để biến đổi vế này thành vế kia.
Ví dụ 1. Cho bốn điểm A, B, C, D bất kì trong không gian. Chứng minh rằng:
\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \)
Lời giải.
\(\begin{array}{l}{\rm{ Ta co }}\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {DB} + \overrightarrow {CB} + \overrightarrow {BD} \\ = \overrightarrow {AD} + \overrightarrow {CB} + \overrightarrow {DB} + \overrightarrow {BD} \\ = \overrightarrow {AD} + \overrightarrow {CB} + \vec 0 = \overrightarrow {AD} + \overrightarrow {CB} \end{array}\)
Ví dụ 2. Cho tứ diện A, B, C, D. Gọi I, J lần lượt là trung điểm của AB, CD
a) Chứng minh rằng : \[\overrightarrow {IJ} = \frac{1}{2}(\overrightarrow {AD} + \overrightarrow {BC} )\]
b) Cho G là trung điểm của I, J. Chứng minh rằng: \(4\overrightarrow {MG} = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} \), với mọi điểm M trong không gian.
Lời giải.
a) Chứng minh rằng: \(\overrightarrow {IJ} = \frac{1}{2}(\overrightarrow {AD} + \overrightarrow {BC} )\)
Ta có \(\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AD} + \mathop {\overrightarrow {DJ} }\limits^2 \) và \(\overrightarrow {IJ} = \overrightarrow {IB} + \overrightarrow {BC} + \overrightarrow {CJ} \)
Suy ra \(2\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AD} + \overrightarrow {DJ} + \overrightarrow {IB} + \overrightarrow {BC} + \overrightarrow {CJ} \)
\(\begin{array}{l} = (\overrightarrow {IA} + \overrightarrow {IB} ) + (\overrightarrow {AD} + \overrightarrow {BC} ) + (\overrightarrow {DJ} + \overrightarrow {CJ} )\\ = \vec 0 + (\overrightarrow {AD} + \overrightarrow {BC} ) + \vec 0 = \overrightarrow {AD} + \overrightarrow {BC} \end{array}\)
b) Cho G là trung điểm của I, J. Chứng minh rằng: \(4\overrightarrow {MG} = \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} \), với mọi điểm M trong không gian.
Tacó
\[\begin{array}{l}\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \\ = 4\overrightarrow {MG} + 2\overrightarrow {GI} + 2\overrightarrow {GJ} = 4\overrightarrow {MG} + 2\vec 0 = 4\overrightarrow {MG} \end{array}\]
(Vì I là trung điểm của AB, J là trung điểm của CD, G là trung điểm của I J)
Dạng 3. Tìm điểm thảo mãn đẳng thức vecto
Phương pháp giải:
Dựa vào các yeus tố cố định như điểm và vecto
– Các bước thực hành giải toán:
1. Biến đổi đẳng thức vecto cho trước về dạng \(\overrightarrow {OM} = \overrightarrow v \)
Trong đó: Điểm O và véc-tơ \(\vec v\) đã biêt.
2. Nếu muốn dụng điểm M, ta lấy O làm gốc dụnng một véc-tơ bằng véc-tơ \(\vec v\), khi đó điểm ngọn của véc-tơ này chính là M.
– Ứng dụng tính chất tâm tỉ cự của hệ điểm
Với các điểm \({A_1},{A_2}, \cdots ,{A_n}\) và các số \({\alpha _1},{\alpha _2}, \cdots ,{\alpha _n}\) thỏa mãn điều kiện \(\sum\limits_{i = 1}^n {{a_i}} \ne 0\).
Tồn tại duy nhất điểm M sao cho: \(\sum\limits_{i = 1}^n {{\alpha _i}} \overrightarrow {M{A_i}} = \vec 0\).
Điểm M như vậy gọi là tâm tỉ cụ̣ của hệ điểm \(\left\{ {{A_1},{A_2}, \cdots ,{A_n}} \right\}\) với các hệ số tương úng là \(\left\{ {{\alpha _1},{\alpha _2}, \cdots ,{\alpha _n}} \right\}\).
Trong trường hợp \({\alpha _i} = {\alpha _j}\forall i,j\) điểm M gọi là trong tâm của hệ điểm \(\left\{ {{A_1},{A_2}, \cdots ,{A_n}} \right\}\).
– Một số kết quả thường sử dụng
Với A, B, C là các điểm cố định, \(\vec v\) là véc-tơ đã biết.
(1) \(\overrightarrow {MA} + \overrightarrow {MB} = \vec 0 \Rightarrow M\) là trung điểm A B
(2) Nếu A, B, C không thẳng hàng thì \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \vec 0 \Rightarrow M\) là trọng tâm tam giác ABC
(3) Tập hợp điểm M \(|\overrightarrow {MA} | = |\overrightarrow {MB} |\) là mặt phẳng trung trực của A B
(4) Tập hợp điểm M thỏa mãn \(|\overrightarrow {MC} | = k|\overrightarrow {AB} |\) là mặt cầu tâm C bán kính bằng k .AB.
Ví dụ 1. Cho hình hộp \(ABCD \cdot \overrightarrow {O{A_1}{B_1}} {C_1}{D_1}\). Xác đinh vị trí của điểm O sao cho:
Lời giải.
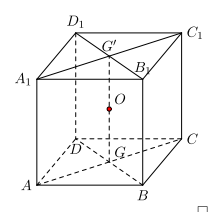
Gọi \(G,{G^\prime }\) là giao điểm các đường chéo của ABCD và \({A_1}{B_1}{C_1}{D_1}\). Khi đó
Ta có:
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} + \overrightarrow {O{A_1}} + \overrightarrow {O{B_1}} + \overrightarrow {O{C_1}} + \overrightarrow {O{D_1}} \)
\( = \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} + \overrightarrow {{G^\prime }{A_1}} + \)
\(\overrightarrow {{G^\prime }{B_1}} + \overrightarrow {{G^\prime }{C_1}} + \overrightarrow {{G^\prime }{D_1}} + 4\left( {\overrightarrow {GO} + \overrightarrow {{G^\prime }O} } \right) = 4\left( {\overrightarrow {GO} + \overrightarrow {{G^\prime }O} } \right) = \vec 0\)
Suy ra O là trung điểm \(G{G^\prime }\).
Ví dụ 2. Cho tứ diện ABCD. Xác định các điểm I, H, G thỏa mãn:
(1) \(\overrightarrow {AI} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
(2) \(\overrightarrow {AH} = \overrightarrow {AB} + \overrightarrow {AC} – \overrightarrow {AD} \).
(3) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0\).
Lời giải
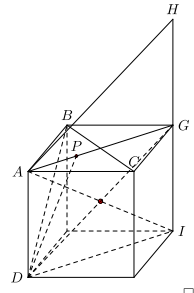
(1) Ta có: \(\overrightarrow {AI} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \)
Mà \((\overrightarrow {AB} + \overrightarrow {AC} ) + \overrightarrow {AD} = \overrightarrow {AG} + \overrightarrow {AD} \) với G là đỉnh còn lại của hình bình hành ABCD vì \(\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {AC} \).
Vậy \(\overrightarrow {AI} = \overrightarrow {AG} + \overrightarrow {AD} \) với I là đỉnh còn lại của hình bình hành AGID
Do đó AI là đường chéo của hình hộp có ba cạnh là AB, AC, AD.
(2) Ta có: \(\overrightarrow {AH} = \overrightarrow {AB} + \overrightarrow {AC} – \overrightarrow {AD} \).
Mà \((\overrightarrow {AB} + \overrightarrow {AC} ) – \overrightarrow {AD} = \overrightarrow {AG} – \overrightarrow {AD} = \overrightarrow {DG} \).
Vậy \(\overrightarrow {AH} = \overrightarrow {DG} \) nên \(F\) là đỉnh còn lại của hình bình hành ADGH
(3) Ta có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = 4\overrightarrow {GP} + \overrightarrow {PD} = \vec 0 \Rightarrow \overrightarrow {PD} = 4\overrightarrow {PG} \) với P là trọng tâm tam giác \(ABC \Rightarrow G\) là điểm nằm trên đoạn thẳng $D P$ sao cho \(PD = 4PG\).
Điểm G thỏa mãn đẳng thức trên gọi là trọng tâm tứ diện.
Ví dụ 3. Trong không gian cho ba điểm A, B, C cố định không thẳng hàng, tìm tập hợp các điểm M sao cho: \(|\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} | = |2\overrightarrow {MA} – \overrightarrow {MB} – \overrightarrow {MC} |\).
Lời giải.
Gọi G là trọng tâm , ta biền đổi đẳng thức về dạng: \(|3\overrightarrow {MG} | = |3\overrightarrow {MA} – 3\overrightarrow {MG} | \Leftrightarrow |\overrightarrow {MG} | = |\overrightarrow {GA} |\)
\( \Rightarrow M\) thuộc mặt cầu tâm G, bán kính GA cố định.
Xem thêm