Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
18 bài tập về khoảng cách từ điểm đến mặt phẳng dạng tổng hợp có đáp án chi tiết
Khoảng cách từ điểm tới mặt
Bài 1. Cho hình chóp S. ABC có ABC là tam giác đều cạnh a . Hai mặt phẳng (SAC),(SAB) cùng vuông góc với đáy và góc tạo bởi SC và đáy bằng 60\[^0\] . Tính khoảng cách từ A tới mặt phẳng (SBC) theo a .
Giải
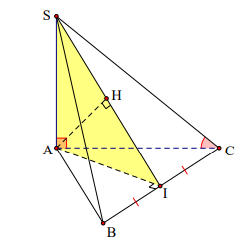
Do \[\left. {\begin{array}{*{20}{c}}{\left( {SAC} \right) \bot \left( {ABC} \right)}\\{\left( {SAB} \right) \bot \left( {ABC} \right)}\\{\left( {SAC} \right) \cap \left( {SAB} \right)}\end{array}} \right\} \Rightarrow SA \bot (ABC)\]
Suy ra góc tạo bởi SC và mặt đáy là
SCA = 30\[^0\]Þ SA = AC.tan SCA = \[a\sqrt 3 \]
Gọi I H, lần lượt là hình chiếu vuông góc của A trên BC, SI khi đó:
\[\left. {\begin{array}{*{20}{c}}{AI \bot BC}\\{SA \bot (ABC) \Rightarrow SA \bot BC}\end{array}} \right\} \Rightarrow BC \bot (SAI) \Rightarrow BC \bot AH\].
Mặt khác AH \[ \bot \] SI nên suy ra AH \[ \bot \] (SBC)
Do đó d(A,(SBC)) = AH. Tam giác ABC đều cạnh a nên AI = \[\frac{{a\sqrt 3 }}{2}\]
Khi đó xét tam giác SAI:
\[\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{I^2}}} = \frac{1}{{3{a^2}}} + \frac{4}{{3{a^2}}} = \frac{5}{{3{a^2}}}\\ \Rightarrow AH = \frac{{a\sqrt {15} }}{5}.\end{array}\]
Vậy d(A,(SBC)) = \[\frac{{a\sqrt {15} }}{5}\].
Bài 2. Cho hình chóp S. ABCD có ABCD hình thang vuông tại A và D . Biết AD = DC = a, AB = 2a ; SA vuông góc với đáy và góc tạo bởi SC và mặt phẳng (SAD) bằng 30\[^0\] . Tính khoảng cách từ A đến mặt phẳng (SBC).
Giải
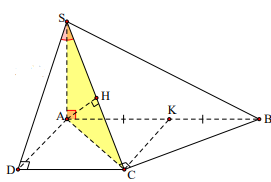
Ta có:
\[\left. {\begin{array}{*{20}{c}}{SA \bot (ABCD) \Rightarrow SA \bot CD}\\{AD \bot CD}\end{array}} \right\} \Rightarrow CD \bot (SAD)\]
Suy ra SD là hình chiếu vuông góc của SC trên mặt phẳng (SAD).
Do đó góc tạo bởi SD và mặt phẳng (SAD) là CSD = \[{30^0}\].
Suy ra: SC = \[\frac{{DC}}{{\sin CSD}} = \frac{a}{{\sin {{30}^0}}} = 2a\]
Gọi K là trung điểm của AB, khi đó
ADCK là hình vuông nên: CK = a = \[\frac{{AC}}{2}\].
Suy ra tam giác ACB vuông tại C hay AC ^ CB
Mặt khác SA ^ CB Þ CB ^ (SAC).
Gọi H là hình chiếu vuông góc của A trên SC
\[ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{CB \bot AH}\\{SC \bot AH}\end{array}} \right. \Rightarrow AH \bot (SBC) \Rightarrow d(A,(SBC)) = AH\]
Ta có AC2 = AD2 + DC2 = 2a2
Þ SA2 = SC2 – AC2 = 4a2 – 2a2 = 2a2
Xét tam giác SAC:
\[\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{1}{{2{a^2}}} + \frac{1}{{2{a^2}}} = \frac{1}{{{a^2}}} \Rightarrow AH = a\]
Vậy d(A,(SBC)) = a.
Nhận xét: Ở ví dụ 2 do AC ^ BC, nên việc dựng hình chiếu của A trên mặt phẳng (SBC) chỉ là công việc dựng hình chiếu của A trên SC như cách làm trên.
Bài 3. Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, \[SD = \frac{{3a}}{2}\], hình chiếu vuông góc của S trên mặt phẳng ABCD là trung điểm của cạnh AB. Tính theo a khoảng cách từ a đến mặt phẳng (SBD).
Giải
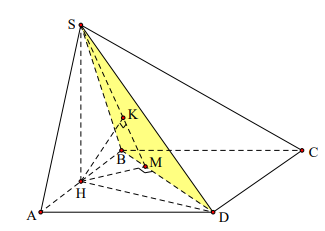
Gọi H là trung điểm của AB Þ SH ^ (ABCD)
AH \[ \cap \](SBD) = {B}Þ \[\frac{{d(A,(SBD))}}{{d(H,(SBD))}} = \frac{{BA}}{{BH}} = 2\]
Þ\[d(A,(SBD)) = 2dd(H,(SBD))\] (1)
Kẻ HM ^ DB (M Î DB) và HK ^ MS (K Î SM)
Khi đó: \[\left\{ {\begin{array}{*{20}{c}}{DB \bot HM}\\{DB \bot SH}\end{array}} \right. \Rightarrow DB \bot (SHM) \Rightarrow DB \bot HK\]
Mà HK ^ SM, do đó:
HK ^ (SBD) Þ d(H,(SBD)) = HK (2)
Xét tam giác HBM ta có:
HM = HB.sin MBH = \[\frac{a}{2}\]sin \[{45^0}\]=\[\frac{{a\sqrt 2 }}{4}\].
Xét tam giác SHM:
\[\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{M^2}}} = \frac{1}{{{a^2}}} + \frac{8}{{{a^2}}} \Rightarrow HK = \frac{a}{3}(3)\]
Từ (1), (2) và (3) suy ra d(A,(SBD)) = \[\frac{{2a}}{3}\].
Bài 4: Cho hình chóp S. ABCD có đáy là hình chữ nhật, AB = a , SA = BC = 2a. Biết hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SBC) .
Giải
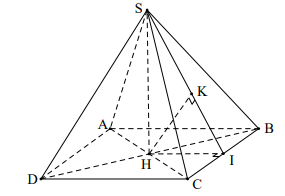
Gọi AC \[ \cap \] BD = {H}.
Ta có: \[\left\{ {\begin{array}{*{20}{c}}{(SAC) \bot (ABCD)}\\{(SBD) \bot (ABCD)}\\{(SAC) \cap (SBD)}\end{array}} \right. \Rightarrow SH \bot (ABCD)\]
Ta có AH = \[\frac{{AC}}{2} = \frac{{\sqrt {A{B^2} + B{C^2}} }}{2} = \frac{{\sqrt {{a^2} + 4{a^2}} }}{2} = \frac{{a\sqrt 5 }}{2}\]
Xét tam giác SAH ta có
SH = \[\sqrt {S{A^2} – A{H^2}} \]= \[\sqrt {4{a^2} – \frac{{5{a^2}}}{4}} = \frac{{a\sqrt {11} }}{2}\]
Do AH \[ \cap \] (SBC) = {C}
Þ \[\frac{{d(A,(SBC))}}{{d(H,(SBC))}} = \frac{{AC}}{{HC}} = 2\]
\[ \Rightarrow d(A,(SBC)) = 2d(H,(SBC))\] (1)
Kẻ HI ^ BC (I Î BC), suy ra
\[\left\{ {\begin{array}{*{20}{c}}{BC \bot HI}\\{BC \bot SH}\end{array}} \right. \Rightarrow BC \bot (SHI)\] và HI = \[\frac{{AB}}{2} = \frac{a}{2}\]
Kẻ HK ^ SI (K Î SI), suy ra
\[\left\{ {\begin{array}{*{20}{c}}{HK \bot BC}\\{HK \bot SI}\end{array}} \right. \Rightarrow HK \bot (SBC)\] Þ d(H,(SBC)) = HK (2)
Xét tam giác SHI, ta có:
\[\begin{array}{l}\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} = \frac{4}{{11{a^2}}} + \frac{4}{{{a^2}}} = \frac{{48}}{{11{a^2}}}\\ \Rightarrow HK = \frac{{a\sqrt {33} }}{{12}}(3)\end{array}\]
Từ (1), (2) và (3) ta được: d(A,(SBC)) = \[\frac{{a\sqrt {33} }}{6}\].
Bài 5. Cho hình chóp S. ABCD có đáy là hình vuông cạnh a , mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SCD).
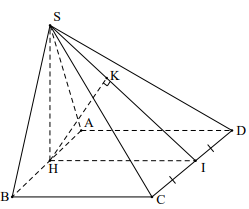
Gọi H là trung điểm của AB Þ SH ^ AB và SH = \[\frac{{a\sqrt 3 }}{2}\]
Ta có \[\left\{ {\begin{array}{*{20}{c}}{(SAB) \bot (ABCD)}\\{(SAB) \cap (ABCD) = AB}\\{(SAB) \supset SH \bot AB}\end{array}} \right. \Rightarrow SH \bot (ABCD)\]
Có AH // CD Þ AH // (SCD) Þ d(A,(SCD)) = d(H,(SCD))
Kẻ HI ^ CD (IÎCD), suy ra CD ^ (SHI)
Kẻ HK ^ SI (KÎSI), suy ra \[\left\{ {\begin{array}{*{20}{c}}{HK \bot CD}\\{HK \bot SI}\end{array}} \right. \Rightarrow HK \bot (SCD)\]
Khi đó d(A,(SCD)) = d(H,(SCD)) = HK.
Ta có HI = AD = a. Xét tam giác SHI ta có
\[\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} = \frac{4}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{7}{{3{a^2}}} \Rightarrow HK = \frac{{a\sqrt {21} }}{7}\]
Vậy d(A,(SCD)) =\[\frac{{a\sqrt {21} }}{7}\].
Bài 6. Cho hình hộp đứng ABCD.A’B’C’D’ có đáy là hình vuông, tam giác A’AC vuông cân, A’C = a. Tính theo a khoảng cách từ điểm A đến mặt phẳng (BCD’).
Giải
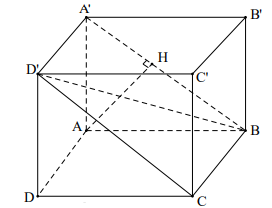
Do tam giác A’AC vuông cân, suy ra AA’ = AC = \[\frac{{A’C}}{{\sqrt 2 }} = \frac{a}{{\sqrt 2 }}\]
Kẻ AH ^ A’B (HÎ A’B) (1)
Do CB ^ (ABB’A’) Þ CB ^ AH (2)
Từ (1) và (2) suy ra AH ^ (BCD’A’)
Þ d(A, (BCD’)) = d(A,(BCD’A’)) = AH
Ta có ABCD là hình vuông nên AB = \[\frac{{AC}}{{\sqrt 2 }} = \frac{a}{2}\]
Xét tam giác ABA’ ta có:
\[\begin{array}{l}\frac{1}{{A{H^2}}} = \frac{1}{{AA{‘^2}}} + \frac{1}{{A{B^2}}} = \frac{2}{{{a^2}}} + \frac{4}{{{a^2}}} = \frac{6}{{{a^2}}}\\ \Rightarrow AK = \frac{{a\sqrt 6 }}{6}\end{array}\]
Vậy d(A, (BCD’)) = \[\frac{{a\sqrt 6 }}{6}\].
Bài 7. Cho hình lăng trụ tam giác . ABC.A’B’C’ có đáy ABC là tam giác vuông tại A và AB = a, BC = 2a. Biết hình chiếu của B’ lên mặt phẳng (ABC) trùng với tâm của đường tròn ngoại tiếp tam giác ABC và góc giữa đường thẳng CC’ và mặt phẳng (A’B’C’) bằng 600 . Tính theo a khoảng cách từ điểm B tới mặt phẳng (B’CA).
Giải
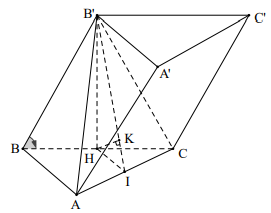
Gọi H là trung điểm của BC.
Do tam giác ABC vuông tại A nên H là tâm của đường tròn ngoại tiếp tam giác ABC
Þ B’H ^ (ABC)
Do BH \[ \cap \] (B’AC) = {C}
Þ\[\frac{{d(B,(B’AC))}}{{d(H,(B’AC))}} = \frac{{BC}}{{HC}} = 2\]
\[ \Rightarrow d(B,(B’AC)) = 2d(H,(B’AC))\] (1)
Kẻ HI ^ AC (I Î AC), suy ra \[AC \bot (B’HI)\]
Kẻ HK ^ B’I (K Î B’I), suy ra:
\[\left\{ {\begin{array}{*{20}{c}}{HK \bot AC}\\{HK \bot B’I}\end{array}} \right. \Rightarrow HK \bot (B’AC) \Rightarrow d(H,(B’AC)) = HK\] (2)
Do \[\left\{ {\begin{array}{*{20}{c}}{CC’//BB’}\\{(A’B’C’)//(ABC)}\end{array}} \right. \Rightarrow (BB’,(ABC)) = (CC’,(A’B’C’)) = {60^0}\]
Khi đó B’H = Bh. tan B’BH = a.tan 600 = \[a\sqrt 3 \]
Ta có HI // BA (vì cùng vuông góc với AC), suy ra HI = \[\frac{{AB}}{2} = \frac{a}{2}\]
Ta có: \[\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{I^2}}} = \frac{1}{{3{a^2}}} + \frac{4}{{{a^2}}} = \frac{{13}}{{3{a^2}}}\]
\[ \Rightarrow HK = \frac{{a\sqrt {39} }}{{13}}\] (3)
Từ (1),(2) và (3), suy ra d(B,(B’AC)) = \[\frac{{2a\sqrt {39} }}{{13}}\].
Bài 8. Cho hình chóp S. ABCD có đáy là hình thoi cạnh a , cạnh bên SA vuông góc với đáy BAD =1200 , M là trung điểm của cạnh BC và SMA= 450 . Tính theo a khoảng cách từ B đến mặt phẳng (SDC).
Giải
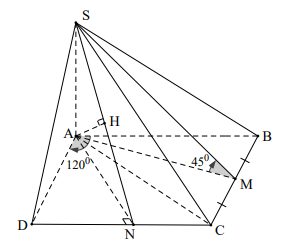
Do AB // DC Þ AB // (SDC)
Þ d(B, (SDC)) = d(A, (SDC)) (1)
Kẻ AN ^ DC (N Î DC)
Do ABCD là hình thoi cạnh a và BAD = 1200 nên ABC, ADC đều là các tam giác đều cạnh a.
Suy ra AM = AN = \[\frac{{a\sqrt 3 }}{2}\]
Khi đó SA = AM.tan BAD = \[\frac{{a\sqrt 3 }}{2}\].tan 450 = \[\frac{{a\sqrt 3 }}{2}\]
Gọi H là hình chiếu vuông góc của A trên SN, khi đó:
\[\left\{ {\begin{array}{*{20}{c}}{CD \bot AN}\\{CD \bot SA}\end{array} \Rightarrow CD \bot (SAN) \Rightarrow CD \bot AH} \right.\]
Mà AH ^ SN Þ AH ^ (SCD) Þ d(A,(SCD)) = AH (2)
Xét tam giác SAN ta có:
\[\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{N^2}}} = \frac{1}{{3{a^2}}} + \frac{4}{{3{a^2}}} = \frac{8}{{3{a^2}}}\]
\[ \Rightarrow AH = \frac{{a\sqrt 6 }}{4}\] (3)
Từ (1),(2) và (3), suy ra d(B,(SCD)) = \[\frac{{a\sqrt 6 }}{4}\].
Bài 9. Cho hình chóp S. ABC, có đáy ABC là hình chóp đều cạnh a . Gọi M là trung điểm của cạnh AB, hình chiếu vuông góc của S trùng với trọng tâm của tam giác MBC , biết SC = \[\frac{{2a}}{3}\]. Tính theo a khoảng cách từ C đến mặt phẳng (SAB).
Giải
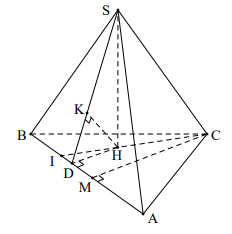
Gọi H là trọng tâm tam giác MBC, suy ra SH ^ (ABC)
Gọi CH \[ \cap \] BM = {I} Þ CH \[ \cap \] (SAB) = {I}
Suy ra \[\frac{{d(C,(SAB))}}{{d(H,(SAB))}} = \frac{{CI}}{{HI}} = 3\]
\[ \Rightarrow d(C,(SAB))) = 3d(H,(SAB))\] (1)
Kẻ HD ^ AB (D Î AB), suy ra \[AB \bot (SHD)\]
Kẻ HK ^ SD (K Î SD), suy ra:
\[\left\{ {\begin{array}{*{20}{c}}{HK \bot AB}\\{HK \bot SD}\end{array}} \right. \Rightarrow HK \bot (SAB) \Rightarrow d(H,(SAB)) = HK\] (2)
Tam giác ABC đều cạnh a nên CM = \[\frac{{a\sqrt 3 }}{2}\]
Ta có HD // CM Þ \[\frac{{HD}}{{CM}} = \frac{{IH}}{{IC}} = \frac{1}{3} \Rightarrow HD = \frac{1}{3}CM = \frac{{a\sqrt 3 }}{6}\]
Do I là trung điểm của BM Þ IM = \[\frac{{AB}}{4}\]= \[\frac{a}{4}\]
Þ CI = \[\sqrt {I{M^2} + C{M^2}} = \sqrt {\frac{{{a^2}}}{{16}} + \frac{{3{a^2}}}{4}} = \frac{{a\sqrt {13} }}{4}\]
Suy ra CH = \[\frac{2}{3}\] CI = \[\frac{{a\sqrt {13} }}{6}\]
Þ SH = \[\sqrt {S{C^2} – C{H^2}} = \sqrt {\frac{{4{a^2}}}{9} – \frac{{13{a^2}}}{{36}}} = \frac{{a\sqrt 3 }}{6}\]
Xét tam giác SHD, ta có
\[\frac{1}{{H{K^2}}} = \frac{1}{{S{H^2}}} + \frac{1}{{H{D^2}}} = \frac{{12}}{{{a^2}}} + \frac{{12}}{{{a^2}}} = \frac{{24}}{{{a^2}}} \Rightarrow HK = \frac{{a\sqrt 6 }}{{12}}\](3)
Từ (1),(2) và (3) ta được d(C,(SAB)) = \[\frac{{a\sqrt 6 }}{4}\]
Xem thêm