Bài giảng về chủ đề Tính khoảng cách từ điểm đến mặt phẳng

Note keypoint

Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bài giảng về chủ đề Tính khoảng cách từ điểm đến mặt phẳng, tài liệu bao gồm 9 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Bài giảng về chủ đề Tính khoảng cách từ điểm đến mặt phẳng

A. LÍ THUYẾT.

CẤP ĐỘ 2: Khoảng cách từ “chân vuông góc” đến “mặt phẳng”

Bài toán trải qua 3 giai đoạn

+) Dựng hình

+) Chứng minh

+) Tính

Cách dựng d(A,SBC)

TH1: Cho hình chóp SABC, SA ^ đáy. Tam giác ABC vuông tại B.

+) Từ A kẻ AH ^ SB (H Î SB) Þ AH = d(A,(SBC))

+) Chứng minh

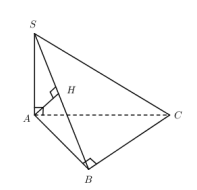
TH2: Cho hình chóp SABC, SA ^ đáy. Tam giác ABC vuông tại C.

+) Từ A kẻ AH ^ SB (H Î SB) Þ AH = d(A,(SBC))

+) Chứng minh

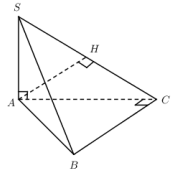
Bài giảng về chủ đề Tính khoảng cách từ điểm đến mặt phẳng (ảnh 2)

TH3: Cho hình chóp SABC, SA ^ đáy. Tam giác ABC không vuông tại B, C.

+) Từ A dựng

$\{\begin{matrix} A M ⊥ B C (M \in B C) \\ A H ⊥ S M (H \in S M) \end{matrix} \Rightarrow A H = d (A, (S B C))$

+) Chứng minh

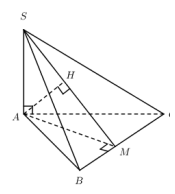
B. BÀI TẬP VÍ DỤ

VD1: Cho hình chóp SABCD, SA ^ (ABCD). Đáy là hình chữ nhật với AB = a, BC = $a \sqrt{3}$ .Góc giữa đường thẳng SC và đáy bằng 45⁰

a) Tính khoảng cách từ A đến mặt phẳng (SBC)

b) Tính khoảng cách từ A đến mặt phẳng (SBD)

c) Tính khoảng cách từ A đến mặt phẳng (SDM) (M là trung điểm của BC)

Hướng dẫn giải

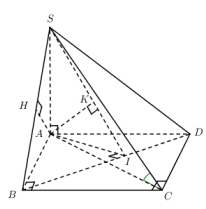
Góc giữa đường thẳng SC và đáy chính là góc giữa đường thẳng SC và đường thẳng AC Þ SCA = 45⁰

a) d(A, SBC) = ?

+) Dựng: AH ^ SB (H Î SB) Þ AH = d(A,(SBC))

+) Chứng minh: AH ^ (SBC)

Ta có:

$\{\begin{matrix} B C ⊥ A B \\ B C ⊥ S A (S A ⊥ (A B C D)) \end{matrix} \Rightarrow B C ⊥ (S A B) \Rightarrow B C ⊥ A H ()$

$\{\begin{matrix} A H ⊥ B C \\ A H ⊥ S B \end{matrix} \Rightarrow A H ⊥ (S B C) \Rightarrow A H = d (A, (S B C))$

+) Tính AH = ?

D ABC : $A C^{2} = A B^{2} + B C^{2} = a^{2} + {(a \sqrt{3})}^{2} \Rightarrow A C = 2 a$

Xét tam giác SAC vuông cân tại A (vì có góc SCA = 45⁰)

Þ SA = AC = 2a

Trong tam giác vuông SAB có: $\frac{1}{A H^{2}} = \frac{1}{S A^{2}} + \frac{1}{A B^{2}}$

$\begin{array}{l} \Rightarrow \frac{1}{A H^{2}} = \frac{1}{4 a^{2}} + \frac{1}{a^{2}} = \frac{5}{4 a^{2}} \Rightarrow A H^{2} = \frac{4 a^{2}}{5} \\ \Rightarrow A H = \frac{2 a}{\sqrt{5}} \Rightarrow d (A, (S B C)) = \frac{2 a}{\sqrt{5}} \end{array}$

b) d(A, SBD) = ?

+) Dựng:

$\{\begin{matrix} A I ⊥ B D (I \in B D) \\ A K ⊥ S I (K \in S I) \end{matrix} \Rightarrow A K = d (A, (S B D)) \Rightarrow B C ⊥ A H$

+) Chứng minh: AK ^ (SBD)

Ta có $\{\begin{matrix} B D ⊥ A I \\ B D ⊥ S A (S A ⊥ (A B C D)) \end{matrix} \Rightarrow B D ⊥ (S A I) \Rightarrow B D ⊥ A K$

$\{\begin{matrix} A K ⊥ B D \\ A K ⊥ S I \end{matrix} \Rightarrow A K ⊥ (S B D) \Rightarrow A K = d (A, (S B D))$

+) Tính AK = ?

Trong tam giác ABD có

$\frac{1}{A I^{2}} = \frac{1}{A B^{2}} + \frac{1}{A D^{2}} = \frac{1}{a^{2}} + \frac{1}{3 a^{2}} = \frac{4}{3 a^{2}}$

$\Rightarrow A I^{2} = \frac{3 a^{2}}{4} \Rightarrow A I = \frac{a \sqrt{3}}{2}$

Trong tam giác SAI có:

$\begin{array}{l} \frac{1}{A K^{2}} = \frac{1}{S A^{2}} + \frac{1}{A I^{2}} = \frac{1}{4 a^{2}} + \frac{1}{3 a^{2}} = \frac{19}{12 a^{2}} \\ \Rightarrow A K = \frac{2 a \sqrt{3}}{\sqrt{19}} \end{array}$

c) d(A, SDM) = ? (M là trung điểm của BC)

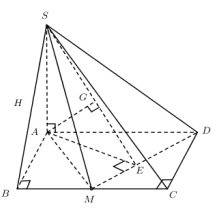
Bài giảng về chủ đề Tính khoảng cách từ điểm đến mặt phẳng (ảnh 5)

+) Dựng: $\{\begin{matrix} A E ⊥ D M \\ A G ⊥ S E \end{matrix} \Rightarrow A G = d (A, (S D M))$

+) Chứng minh: HS tự chứng minh

+) Tính AG = ? Xét tam giác DMC:

DM² = DC² + CM² = a² + ${(\frac{a \sqrt{3}}{2})}^{2}$ = $\frac{7 a^{2}}{4}$

Þ DM = $\frac{a \sqrt{7}}{2}$

Ta có:

S_DADM = $\frac{1}{2}$ DM.AE = $\frac{1}{2}$ AD.AB

Þ AE = $\frac{A D . A B}{D M} = \frac{a^{2} \sqrt{3}}{\frac{a \sqrt{7}}{2}} = \frac{2 a \sqrt{3}}{\sqrt{7}}$

Trong tam giác SAE có:

$\begin{array}{l} \frac{1}{A G^{2}} = \frac{1}{S A^{2}} + \frac{1}{A E^{2}} = \frac{1}{4 a^{2}} + \frac{1}{{(\frac{2 a \sqrt{3}}{\sqrt{7}})}^{2}} \\ = \frac{1}{4 a^{2}} + \frac{7}{12 a^{2}} = \frac{10}{12 a^{2}} = \frac{5}{6 a^{2}} \\ \Rightarrow A G^{2} = \frac{5}{6 a^{2}} \Rightarrow A G = \frac{a \sqrt{6}}{\sqrt{5}} \end{array}$

VD2: Cho hình chóp SABCD có đáy là hình thang vuông tại A, B và AB = 2a, BC = 2a, AD = 4a. Gọi H là trung điểm của AC, SH ^ đáy, SA = 2a

a) Tính khoảng cách từ H đến mặt phẳng (SCD)

b) Tính khoảng cách từ H đến mặt phẳng (SAB)

Hướng dẫn giải

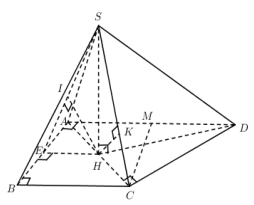
Gọi M là trung điểm của AD

+) Xét tứ giác AMCB có: $\{\begin{matrix} A M ∥ B C \\ A M = B C \\ A = 90^{0} \\ A B = B C = 2 a \end{matrix}$

ÞTứ giác AMCB là hình vuông

Þ CM = 2a.

+) Xét tam giác ACD:

CM = $\frac{1}{2}$ AD ÞD ACD vuông tại C

Þ AC ^ CD

a) d(H, SCD) = ?

+) Dựng: Từ H dựng HK ^ SC (K Î SC) Þ HK = d(H,(SCD))

+) Chứng minh: HS tự làm

+) Tính:

DABC : AC² + BC² = (2a)² + (2a)² = 8a²

Þ AC = 2a $\sqrt{2}$ Þ HC = $\frac{A C}{2} = a \sqrt{2}$

DSAH : SH² = SA² – AH² = 4a² – 2a² = 2a²

Þ SH = a $\sqrt{2}$

DSHC:

$\begin{array}{l} \frac{1}{H K^{2}} = \frac{1}{S H^{2}} + \frac{1}{H C^{2}} = \frac{1}{2 a^{2}} + \frac{1}{2 a^{2}} = \frac{1}{a^{2}} \\ \Rightarrow H K = a \end{array}$

b) d(H, SAB) = ?

+) Dựng: $\{\begin{matrix} H E ⊥ A B (E \in A B) \\ H I ⊥ S E (I \in S E) \end{matrix} \Rightarrow H I = d (H, (S A B))$

+) Chứng minh: HS tự làm

+) Tính: HE là đường trung bình của tam giác ABC

Þ HE = $\frac{1}{2} B C = \frac{2 a}{2} = a$

Trong tam giác SHE:

$\frac{1}{H I^{2}} = \frac{1}{S H^{2}} + \frac{1}{H E^{2}} = \frac{1}{2 a^{2}} + \frac{1}{a^{2}} = \frac{3}{2 a^{2}} \Rightarrow H I = \frac{a \sqrt{2}}{\sqrt{3}}$

BÀI TẬP TỰ LUYỆN

Bài 1: Cho hình chóp SABCD có SA \[ \bot \] (ABCD). Đáy là hình chữ nhật với AB = a, AD = \[a\sqrt 3 \].Góc giữa SC và đáy bằng 45⁰

1. Khoảng cách từ điểm A đến (SBC)

A. \[a\sqrt 2 \]

B. \[\frac{{2a}}{{\sqrt 5 }}\]

C. \[\frac{{2a}}{5}\]

D. 5a

2. Khoảng cách từ điểm A đến (SBD)

A. \[\frac{a}{{\sqrt {19} }}\]

B. \[\frac{{2a\sqrt 2 }}{{19}}\]

C. \[\frac{{2a\sqrt 3 }}{{\sqrt {19} }}\]

D. \[a\sqrt 3 \]

3. Khoảng cách từ điểm A đến (SDM) với M là trung điểm BC

A. \[\frac{{2a}}{{\sqrt {10} }}\]

B. \[\frac{{a\sqrt 3 }}{5}\]

C. \[\frac{{2a\sqrt 3 }}{{\sqrt {10} }}\]

D. \[\frac{a}{{10}}\]

Bài 2: Cho hình chóp S.ABC có hai mặt phẳng (SAB), (SAC) cùng vuông góc với đáy. Đáy là tam giác ABC có góc A = 120⁰ , AB = a, AC = 2a. Góc giữa SC và đáy bằng 60⁰. Sau khi rút gọn tối giản, mẫu số của khoảng cách từ A đến (SBC) nhận giá trị nào dưới đây

A. 27

B. 28

C. 29

D. 30

Bài 3: Cho lăng trụ đứng ABCA’B’C’ có đáy là tam giác vuông tại B với AB = a, BC = \[a\sqrt 3 \], A’B = \[a\sqrt 3 \].

1. Gọi khoảng cách từ điểm B đến mặt phẳng (A’C’AC) là X. Giá trị của biểu thức \[\frac{{4{X^2}}}{{{a^2}}}\]là:

A. 2

B. 3

C. 4

D. 5

2. Khoảng cách từ điểm B đến mặt phẳng (B’AC) có giá trị bằng

A. \[\frac{{a\sqrt 6 }}{{\sqrt {11} }}\]

B. \[\frac{{a\sqrt {11} }}{{\sqrt 6 }}\]

C. \[\frac{a}{{\sqrt 6 }}\]

D. \[a\sqrt {11} \]

Bài 4: Cho hình chóp S.ABC có đáy là tam giác đều cạnh 2a, cạnh bên bằng 3a. Gọi O là tâm đường tròn ngoại tiếp của mặt đáy.

1. Thể tích của khối chóp này là:

A. \[{a^3}\sqrt {23} \]

B. \[3{a^3}\sqrt {23} \]

C. \[\frac{{{a^3}\sqrt {23} }}{3}\]

D. \[\frac{{3{a^3}}}{{\sqrt {23} }}\]

2. Tính khoảng cách từ O đến (SAB) :

A. \[\frac{{a\sqrt {42} }}{{23}}\]

B. \[\frac{{a\sqrt {43} }}{{26}}\]

C. \[\frac{{a\sqrt {46} }}{{12}}\]

D. \[\frac{{a\sqrt {23} }}{{46}}\]

3. Gọi M,N lần lượt là trung điểm BC, AB . Tính khoảng cách từ O đến mặt phẳng (SMN) . Khoảng cách này có giá trị của mẫu số sau khi tối giản là:

A. 90

B. 91

C. 92

D. 93

Bài 5: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, B với AB = BC = 2a, AD = 4a. Gọi H là trung điểm của AC. Biết SH ^ (ABCD). Góc giữa SC và đáy bằng 45⁰.

1.Độ dài khoảng cách từ điểm H đến mặt phẳng (SCD) là :

A. a

B. 2a

C. \[a\sqrt 2 \]

D. \[\frac{{a\sqrt 2 }}{2}\]

2. Khoảng cách từ H đến mặt phẳng (SAB) nhận giá trị là :

A. \[\frac{{\sqrt 2 a}}{{\sqrt 3 }}\]

B. \[2a\sqrt 3 \]

C. \[\frac{{a\sqrt 3 }}{4}\]

D. \[a\sqrt 3 \]

HƯỚNG DẪN GIẢI CHI TIẾT

Bài 1: Hướng dẫn giải 1.

Ta có (SC;(ABCD)) = (SC;AC) = SCA = 45⁰

Ta có \[\left\{ {\begin{array}{*{20}{c}}{BC \bot AB}\\{BC \bot SA(SA \bot (ABC{\rm{D}}))}\end{array}} \right. \Rightarrow BC \bot (SAB)\]

Trong (SAB) kẻ AH ^ SB (H Î SB) ta có:

\[\left\{ {\begin{array}{*{20}{c}}{BC \bot AH(BC \bot (SAB))}\\{AH \bot SB}\end{array}} \right.\]

\[ \Rightarrow AH \bot (SBC) \Rightarrow d(A;(SBC)) = AH\]

Tam giác SAC vuông cân tại A nên SA = AC = \[\sqrt {A{B^2} + A{C^2}} = 2a\]

Áp dụng hệ thức lượng trong tam giác vuông SAB có :

AH = \[\frac{{SA.AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{2a}}{{\sqrt 5 }}\]

Þ d(A;(SBC)) = \[\frac{{2a}}{{\sqrt 5 }}\]

Chọn B.

Xem thêm

Bài liên quan:

Leave a Comment Hủy