Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu bao gồm các nội dung sau:
Tập 1. Vecto trong không gian
A. Tóm tắt giáo khoa
B. Luyện kĩ năng giải các dạng bài tập
Bài toán 1: Chứng minh đẳng thức vecto
Bài toán 2: Chứng minh va vecto đồng phẳng và bốn điểm đồng phẳng
Bài toán 3: Tính độ dài của đoạn thẳng
Bài toán 4: Sử dụng điều kiện đồng phẳng của bốn điểm để giải bài toán hình không gian.
Chuyên đề vector trong không gian – quan hệ vuông góc phần 2
Chương III. Vec tơ trong không gian
Quan hệ vuông góc trong không gian
Tập 1. Vecto trong không gian
A. Chuẩn kiến thức
A. Tóm tȧt giáo khoa.
I. Định nghĩa.
Các khái niện và các phép toán của vec tơ trong không gian được định nghĩa hoàn toàn giống như trong mặt phẳng.Ngoài ra ta cần nhớ thêm:
1. Qui tắc hình hộp : Nếu ABCD.A’B’ \({{\rm{C}}^\prime }{{\rm{D}}^\prime }\) là hình hộp thì \(\overrightarrow {{\rm{A}}{{\rm{C}}^\prime }} = \overrightarrow {{\rm{AB}}} + \overrightarrow {{\rm{AD}}} + \overrightarrow {{\rm{A}}{{\rm{A}}^\prime }} = \vec a + \vec b + \vec c\).
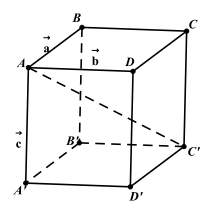
2. Qui tắc trọng tâm tứ diện.
G là trọng tâm tứ diện ABCD khi và chỉ khi một trong hai điều kiện sau
xảy ra:
– \(\quad \overrightarrow {{\rm{GA}}} + \overrightarrow {{\rm{GB}}} + \overrightarrow {{\rm{GC}}} + \overrightarrow {{\rm{GD}}} = \vec 0\)
– \(\quad \overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{MB}}} + \overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MD}}} = 4\overrightarrow {{\rm{MG}}} ,\forall {\rm{M}}\)
3. Ba véc to \(\vec a,\vec b,\vec c\) đồng phẳng nếu giá của chúng song song với một mặt phẳng.
Điều kiện cần và đủ để ba véc to \(\vec a,\vec b,\vec c\) đồng phẳng là có các số m, n, p không đồng thời bằng 0 sao cho \(m\vec a + n\vec b + \overrightarrow {pc} = \vec 0\).
Cho hai vec tơ không cùng phương khi đó điều kiện cần và đủ để ba vec tơ \(\vec a,\vec b,\vec c\) đồng phẳng là có các số m,n sao cho \(\overrightarrow {\rm{c}} = {\rm{ma}} + {\rm{n}}\overrightarrow {\rm{b}} \).
Nếu ba véc to \(\overrightarrow {\rm{a}} ,\overrightarrow {\rm{b}} ,\vec c\) không đồng phẳng thì mỗi vec to \(\overrightarrow {\rm{d}} \) đều có thể phân tích một cách duy nhất dưới dạng \(\vec d = m\vec a + n\vec b + \overrightarrow {pc} \).
B. Luyện kĩ năng giải các dạng bài tâp.
Bài toán 01: Chứng minh đẳng thức vec tơ.
Phương pháp:
Sử dụng qui tắc cộng, qui tắc trừ ba điểm, qui tắc trung điểm đoạn thẳng, trọng tâm tam giác, trọng tâm tứ giác, qui tắc hình bình hành, qui tắc hình hộp…để biến đổi vế này thành vế kia.
Các ví dụ
Ví dụ 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Chứng minh rằng \({\overrightarrow {{\rm{SA}}} ^2} + {\overrightarrow {{\rm{SC}}} ^2} = {\overrightarrow {{\rm{SB}}} ^2} + {\overrightarrow {{\rm{SD}}} ^2}\).
Lời giải.
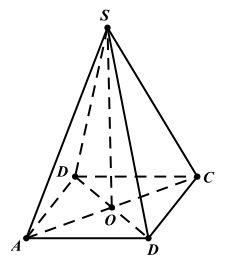
Gọi O là tâm của hình chữ nhật ABCD
Ta có \(|\overrightarrow {{\rm{OA}}} | = |\overrightarrow {{\rm{OB}}} | = |\overrightarrow {{\rm{OC}}} | = |\overrightarrow {{\rm{OD}}} |\).
\({\overrightarrow {{\rm{SA}}} ^2} = {(\overrightarrow {{\rm{SO}}} + \overrightarrow {{\rm{OA}}} )^2} = {\overrightarrow {{\rm{SO}}} ^2} + {\overrightarrow {{\rm{OA}}} ^2} + 2\overrightarrow {{\rm{SO}}} \cdot \overrightarrow {{\rm{OA}}} (1)\)
\({\overrightarrow {{\rm{SC}}} ^2} = {(\overrightarrow {{\rm{SO}}} + \overrightarrow {{\rm{OC}}} )^2} = {\overrightarrow {{\rm{SO}}} ^2} + {\overrightarrow {{\rm{OC}}} ^2} + 2\overrightarrow {{\rm{SO}}} \cdot \overrightarrow {{\rm{OC}}} (2)\)
Từ \((1)\) và \((2)\) suy ra
\({\overrightarrow {{\rm{SA}}} ^2} + {\overrightarrow {{\rm{SC}}} ^2} = 2{\overrightarrow {{\rm{SO}}} ^2} + {\overrightarrow {{\rm{OA}}} ^2} + {\overrightarrow {{\rm{OC}}} ^2} + 2\overrightarrow {{\rm{SO}}} (\overrightarrow {{\rm{OA}}} + \overrightarrow {{\rm{OC}}} )\)
\( = 2{\overrightarrow {{\rm{SO}}} ^2} + {\overrightarrow {{\rm{OA}}} ^2} + {\overrightarrow {{\rm{OC}}} ^2}(\) vì \(\overrightarrow {{\rm{OA}}} + \overrightarrow {{\rm{OC}}} = \vec 0)\)
Tương tự \({\overrightarrow {{\rm{SB}}} ^2} + {\overrightarrow {{\rm{SD}}} ^2} = 2{\overrightarrow {{\rm{SO}}} ^2} + {\overrightarrow {{\rm{OB}}} ^2} + {\overrightarrow {{\rm{OD}}} ^2}\).
Từ đó suy ra \({\overrightarrow {{\rm{SA}}} ^2} + {\overrightarrow {{\rm{SC}}} ^2} = {\overrightarrow {{\rm{SB}}} ^2} + {\overrightarrow {{\rm{SD}}} ^2}\).
Ví dụ 2. Cho tứ diện ABCD,M và N lần lượt là các điểm thuộc các cạnh AB và CD sao cho \(\overrightarrow {{\rm{MA}}} = – 2\overrightarrow {{\rm{MB}}} ,\overrightarrow {{\rm{ND}}} = – 2\overrightarrow {{\rm{NC}}} \); các điểm I,J,K lần lượt thuộc AD,MN,BC sao cho \(\overrightarrow {{\rm{IA}}} = {\rm{kID}},\overrightarrow {{\rm{JM}}} = {\rm{kJN}},\overrightarrow {{\rm{KB}}} = {\rm{kKC}}\). Chứng minh với mọi điểm O ta có \(\overrightarrow {{\rm{OJ}}} = \frac{1}{3}\overrightarrow {{\rm{OI}}} + \frac{2}{3}\overrightarrow {{\rm{OK}}} \).
Lời giải.
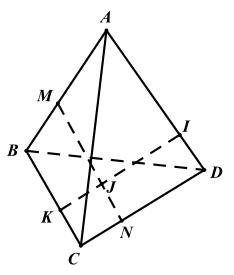
Vì \(\overrightarrow {{\rm{MA}}} = – 2\overrightarrow {{\rm{MB}}} \) nên với điểm O bất kì ta có \(\overrightarrow {{\rm{OA}}} – \overrightarrow {{\rm{OM}}} = – 2(\overrightarrow {{\rm{OB}}} – \overrightarrow {{\rm{OM}}} )\)
\( \Leftrightarrow \overrightarrow {{\rm{OM}}} = \frac{{\overrightarrow {{\rm{OA}}} + 2\overrightarrow {{\rm{OB}}} }}{3}\)
Từ đó ta có \(\overrightarrow {{\rm{OJ}}} = \frac{1}{{1 – {\rm{k}}}} \cdot \frac{1}{3}(\overrightarrow {{\rm{OA}}} + 2\overrightarrow {{\rm{OB}}} – {\rm{k}}\overrightarrow {{\rm{OD}}} – 2{\rm{k}}\overrightarrow {{\rm{OC}}} )\)
\(\overrightarrow {{\rm{ON}}} = \frac{{\overrightarrow {{\rm{OD}}} + 2\overrightarrow {{\rm{OC}}} }}{3},\overrightarrow {{\rm{OI}}} = \frac{{\overrightarrow {{\rm{OA}}} – {\rm{k}}\overrightarrow {{\rm{OD}}} }}{{1 – {\rm{k}}}},\)
\(\overrightarrow {{\rm{OK}}} = \frac{{\overrightarrow {{\rm{OB}}} – {\rm{k}}\overrightarrow {{\rm{OC}}} }}{{1 – {\rm{k}}}},\overrightarrow {{\rm{OJ}}} = \frac{{\overrightarrow {{\rm{OM}}} – {\rm{k}}\overrightarrow {{\rm{ON}}} }}{{1 – {\rm{k}}}}.\)
\( = \frac{1}{{1 – {\rm{k}}}} \cdot \frac{1}{3}[(1 – {\rm{k}})\overrightarrow {{\rm{OI}}} + 2(1 – {\rm{k}})\overrightarrow {{\rm{OK}}} ] = \frac{1}{3}(\overrightarrow {{\rm{OI}}} + 2\overrightarrow {{\rm{OK}}} )\)
Vậy \(\overrightarrow {{\rm{OJ}}} = \frac{1}{3}\overrightarrow {{\rm{OI}}} + \frac{2}{3}\overrightarrow {{\rm{OK}}} \).
Bài toán 02: Chứng minh ba vec tơ đồng phẳng và bốn điểm đồng phẳng.
Phương pháp:
Để chứng minh ba vec to \(\vec a,\vec b,\vec c\) đồng phẳng ta có thể thực hiện theo một trong các cách sau:
– Chứng minh giá của ba vec tơ \(\vec a,\vec b,\vec c\) cùng song song với một mặt phẳng.
– Phân tích \(\vec c = m\vec a + n\vec b\) trong đó \(\vec a,\vec b\) là hai vec to không cùng phương.
Để chứng minh bốn điểm A,B,C,D đồng phẳng ta có thể chứng minh ba vecto \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{AC}}} ,\overrightarrow {{\rm{AD}}} \) đồng phẳng. Ngoài ra có thể sử dụng kết quả quen thuộc sau:
Điều kiện cần và đủ để điểm \({\rm{D}} \in ({\rm{ABC}})\) là với mọi điểm O bất kì ta có \(\overrightarrow {{\rm{OD}}} = x\overrightarrow {{\rm{OA}}} + y\overrightarrow {{\rm{OB}}} + {\rm{zOC}}\) trong đó x + y + z = 1.
Các ví dụ
Ví dụ 1. Cho tứ diện ABCD, các điểm M, N lần lượt là trung điểm của AB, CD. Gọi P, Q lần lượt là các điểm thỏa mãn \(\overrightarrow {{\rm{PA}}} = {\rm{kPD}},\overrightarrow {{\rm{QB}}} = {\rm{kQC}}({\rm{k}} \ne 1)\). Chứng minh M,N,P,Q đồng phẳng.
Lời giải.
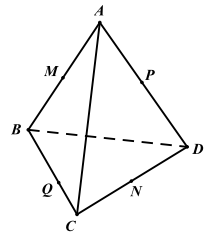
Ta có \(\overrightarrow {{\rm{PA}}} = {\rm{kPD}} \Rightarrow \overrightarrow {{\rm{MA}}} – \overrightarrow {{\rm{MP}}} = {\rm{k}}(\overrightarrow {{\rm{MD}}} – \overrightarrow {{\rm{MP}}} )\)
\( \Leftrightarrow \overrightarrow {{\rm{MP}}} = \frac{{\overrightarrow {{\rm{MA}}} – {\rm{kMD}}}}{{1 – {\rm{k}}}}.\)
Tưong tự \(\overrightarrow {{\rm{QB}}} = {\rm{kQC}} \Rightarrow \overrightarrow {{\rm{MQ}}} = \frac{{\overrightarrow {{\rm{MA}}} – {\rm{kMC}}}}{{1 – {\rm{k}}}}\)
Suy ra \(\overrightarrow {{\rm{MP}}} + \overrightarrow {{\rm{MQ}}} = \frac{{\overrightarrow {{\rm{MA}}} – {\rm{kMD}} + \overrightarrow {{\rm{MB}}} – {\rm{kMC}}}}{{1 – {\rm{k}}}}\)
\( = \frac{k}{{{\rm{k}} – 1}}(\overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MD}}} )({\rm{Do}}\overrightarrow {{\rm{MA}}} + \overrightarrow {{\rm{MB}}} = \vec 0)\)
Mặt khác N là trung điểm của CD nên \(\overrightarrow {{\rm{MC}}} + \overrightarrow {{\rm{MD}}} = 2\overrightarrow {{\rm{MN}}} \Rightarrow \overrightarrow {{\rm{MP}}} + \overrightarrow {{\rm{MQ}}} = \frac{{2{\rm{k}}}}{{{\rm{k}} – 1}}\overrightarrow {{\rm{MN}}} \)
suy ra ba vec tơ \(\overrightarrow {{\rm{MP}}} ,\overrightarrow {{\rm{MQ}}} ,\overrightarrow {{\rm{MN}}} \) đồng phẳng, hay bốn điểm M,N,P.Q đồng phẳng.
Ví dụ 2. Cho tứ diện ABCD, các điểm M,N xác định bởi \(\overrightarrow {{\rm{MA}}} = {\rm{xMC}},\overrightarrow {{\rm{NB}}} = {\rm{y}}\overrightarrow {{\rm{ND}}} ({\rm{x}},{\rm{y}} \ne 1)\). Tìm điều kiện giữa x và y để ba vecto \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{CD}}} ,\overrightarrow {{\rm{MN}}} \) đồng phẳng.
Lời giải.
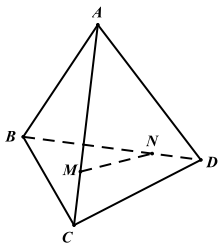
Đặt \(\overrightarrow {{\rm{DA}}} = \overrightarrow {\rm{a}} ,\overrightarrow {{\rm{DB}}} = \overrightarrow {\rm{b}} ,\overrightarrow {{\rm{DC}}} = \overrightarrow {\rm{c}} \) thì \(\overrightarrow {\rm{a}} ,\overrightarrow {\rm{b}} ,\overrightarrow {\rm{c}} \) không đồng phẳng.
\(\overrightarrow {{\rm{MA}}} = x\overrightarrow {{\rm{MC}}} \Rightarrow \overrightarrow {{\rm{DA}}} – \overrightarrow {{\rm{DM}}} = x(\overrightarrow {{\rm{DC}}} – \overrightarrow {{\rm{DM}}} )\)
\( \Rightarrow \overrightarrow {{\rm{DM}}} = \frac{{\overrightarrow {{\rm{DA}}} – x\overrightarrow {{\rm{DC}}} }}{{1 – x}} = \frac{{\overrightarrow {\rm{a}} – {\rm{xc}}}}{{1 – {\rm{c}}}}\)(1)
Lại có \(\overrightarrow {{\rm{NB}}} = {\rm{yND}} \Rightarrow \overrightarrow {{\rm{DN}}} = \frac{1}{{1 – {\rm{y}}}}\overrightarrow {{\rm{DB}}} = \frac{1}{{1 – {\rm{y}}}}\overrightarrow {\rm{b}} \)(2)
Từ (1) và (2) suy ra
\(\overrightarrow {{\rm{MN}}} = \overrightarrow {{\rm{DN}}} – \overrightarrow {{\rm{DM}}} = \frac{{ – 1}}{{1 – x}}\overrightarrow {\rm{a}} + \frac{1}{{1 – {\rm{y}}}}\overrightarrow {\rm{b}} + \frac{{\rm{x}}}{{1 – {\rm{x}}}}\overrightarrow {\rm{c}} \).
Ta có \(\overrightarrow {{\rm{AB}}} = \overrightarrow {{\rm{DB}}} – \overrightarrow {{\rm{DA}}} = \overrightarrow {\rm{b}} – \overrightarrow {\rm{a}} ,\overrightarrow {{\rm{CD}}} = – \overrightarrow {\rm{c}} ;\overrightarrow {{\rm{AB}}} \) và \(\overrightarrow {{\rm{CD}}} \) là hai vecto không cùng phương nên \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{CD}}} ,\overrightarrow {{\rm{MN}}} \) đồng phẳng khi và chỉ khi \(\overrightarrow {{\rm{MN}}} = {\rm{m}}\overrightarrow {{\rm{AB}}} + {\rm{nCD}}\), tức là \(\frac{{ – 1}}{{1 – {\rm{x}}}}\overrightarrow {\rm{a}} + \frac{1}{{1 – {\rm{y}}}}\overrightarrow {\rm{b}} + \frac{{\rm{x}}}{{1 – {\rm{x}}}}\overrightarrow {\rm{c}} = {\rm{m}}(\overrightarrow {\rm{b}} – \overrightarrow {\rm{a}} ) – {\rm{nc}}\)
\(\begin{array}{l} \Leftrightarrow \left( {m – \frac{1}{{1 – x}}} \right)\vec a + \left( {\frac{1}{{1 – y}} – m} \right)\vec b + \left( {n + \frac{x}{{1 – x}}} \right)\vec c = \vec 0\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m = \frac{1}{{1 – x}}}\\{m = \frac{1}{{1 – y}}}\\{n = – \frac{x}{{1 – x}}}\end{array}x = y} \right.\end{array}\)
Vậy ba vec to \(\overrightarrow {{\rm{AB}}} ,\overrightarrow {{\rm{CD}}} ,\overrightarrow {{\rm{MN}}} \) đồng phẳng khi và chỉ khi x = y.
Lưu ý : Ta có thể sử dụng điều kiện đồng phẳng của ba vec tơ để xét vị trí tương đối của đường thẳng với mặt phẳng:
Cho ba đường thẳng \({{\rm{d}}_1},\;{{\rm{d}}_2},\;{{\rm{d}}_3}\) lần lượt chứa ba vec to \(\overrightarrow {{{\rm{u}}_1}} ,\overrightarrow {{{\rm{u}}_2}} ,\overrightarrow {{{\rm{u}}_3}} \) trong đó \({{\rm{d}}_1},\;{{\rm{d}}_2}\) cắt nhau và \({{\rm{d}}_3}\not \subset {\mathop{\rm mp}\nolimits} \left( {{{\rm{d}}_1},\;{{\rm{d}}_2}} \right)\)
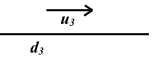
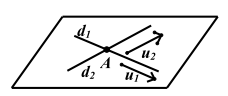
Khi đó :
– \(\quad {{\rm{d}}_3}//\left( {{{\rm{d}}_1},\;{{\rm{d}}_2}} \right) \Leftrightarrow \overrightarrow {{{\rm{u}}_1}} ,\overrightarrow {{{\rm{u}}_2}} ,\overrightarrow {{{\rm{u}}_3}} \) là ba vec tơ đồng phẳng.
– \(\quad {{\rm{d}}_3} \cap {\rm{mp}}\left( {{{\rm{d}}_1},\;{{\rm{d}}_2}} \right) = {\rm{M}} \Leftrightarrow \overrightarrow {{{\rm{u}}_1}} ,\overrightarrow {{{\rm{u}}_2}} ,\overrightarrow {{{\rm{u}}_3}} \) là ba vec to không đồng phẳng
Ví dụ 3. Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime },M,N\) là các điểm thỏa \(\overrightarrow {{\rm{MA}}} = – \frac{1}{4}\overrightarrow {{\rm{MD}}} ,\overrightarrow {{\rm{NA}}} = – \frac{2}{3}\overrightarrow {{\rm{NC}}} \). Chứng \({\mathop{\rm minh}\nolimits} {\rm{MN}}//\left( {{\rm{B}}{{\rm{C}}^\prime }{\rm{D}}} \right)\)
Lời giải.
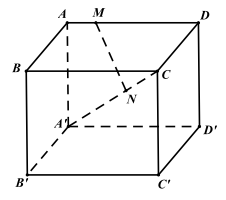
Đặt \(\overrightarrow {{\rm{BA}}} = \overrightarrow {\rm{a}} ,\overrightarrow {{\rm{B}}{{\rm{B}}^\prime }} = \overrightarrow {\rm{b}} ,\overrightarrow {{\rm{BC}}} = \overrightarrow {\rm{c}} \) thì \(\overrightarrow {\rm{a}} ,\overrightarrow {\rm{b}} ,\overrightarrow {\rm{c}} \) là ba vec to không đồng phẳng và \(\overrightarrow {{\rm{BD}}} = \overrightarrow {{\rm{BA}}} + \overrightarrow {{\rm{AD}}} = \overrightarrow {{\rm{BA}}} + \overrightarrow {{\rm{BC}}} = \overrightarrow {\rm{a}} + \overrightarrow {\rm{c}} \)
\(\overrightarrow {{\rm{B}}{{\rm{C}}^\prime }} = \overrightarrow {\rm{b}} + \overrightarrow {\rm{c}} ,\overrightarrow {{\rm{BA}}} = \overrightarrow {\rm{a}} + \overrightarrow {\rm{b}} \)
Ta có
\(\begin{array}{l}\overrightarrow {{\rm{MA}}} = – \frac{1}{4}\overrightarrow {{\rm{MD}}} \Rightarrow \overrightarrow {{\rm{BA}}} – \overrightarrow {{\rm{BM}}} = – \frac{1}{4}(\overrightarrow {{\rm{BD}}} – \overrightarrow {{\rm{BM}}} )\\ \Rightarrow \frac{5}{4}\overrightarrow {{\rm{BM}}} = \overrightarrow {{\rm{BA}}} + \frac{1}{4}\overrightarrow {{\rm{BD}}} \end{array}\)
\( \Rightarrow \overrightarrow {{\rm{BM}}} = \frac{{4\overrightarrow {{\rm{BA}}} + \overrightarrow {{\rm{BD}}} }}{5} = \frac{{4\overrightarrow {\rm{a}} + (\overrightarrow {\rm{a}} + \overrightarrow {\rm{c}} )}}{5} = \frac{{5\overrightarrow {\rm{a}} + \overrightarrow {\rm{c}} }}{5}.\)
Tương tự
\(\begin{array}{l}\overrightarrow {{\rm{BN}}} = \frac{{3\overrightarrow {\rm{a}} + 3\overrightarrow {\rm{b}} + 2\overrightarrow {\rm{c}} }}{5},\\{\rm{MN}} = {\rm{BN}} – {\rm{BM}} = \frac{{ – 2{\rm{a}} + 3\;{\rm{b}} + {\rm{c}}}}{5}\\ = – \frac{2}{5}({\rm{a}} + {\rm{c}}) + \frac{3}{5}(\;{\rm{b}} + {\rm{c}}) = – \frac{2}{5}{\rm{BD}} + \frac{3}{5}{\rm{BC}}\end{array}\)
Suy ra \(\overrightarrow {{\rm{MN}}} ,\overrightarrow {{\rm{DB}}} ,\overrightarrow {{\rm{B}}{{\rm{C}}^\prime }} \) đồng phẳng mà \({\rm{N}} \notin \left( {{\rm{B}}{{\rm{C}}^\prime }{\rm{D}}} \right) \Rightarrow {\rm{MN}}//\left( {{\rm{B}}{{\rm{C}}^\prime }{\rm{D}}} \right)\).
Nhận xét: Có thể sử dụng phương pháp trên để chứng minh hai mặt phẳng song song.
Ví dụ 4. Cho lăng trụ tam giác ABC. \({A^\prime }{B^\prime }{C^\prime }\). Gọi M, N lần lượt là trung điểm của \(A{A^\prime },C{C^\prime }\) và G là trọng tâm của tam giác \({A^\prime }{B^\prime }{C^\prime }\). Chứng minh \(\left( {{\rm{MG}}{{\rm{C}}^\prime }} \right)//\left( {{\rm{A}}{{\rm{B}}^\prime }{\rm{N}}} \right)\).
Lời giải.
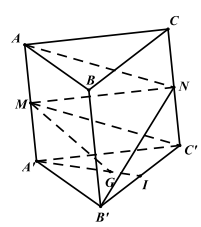
Đặt \(\overrightarrow {{\rm{A}}{{\rm{A}}^\prime }} = \vec a,\overrightarrow {{\rm{AB}}} = \vec b,\overrightarrow {{\rm{AC}}} = \overrightarrow {\rm{c}} \)
Vì M,N lần lượt là trung điểm của \({\rm{A}}{{\rm{A}}^\prime },{\rm{C}}{{\rm{C}}^\prime }\) nên \(\overrightarrow {{\rm{AM}}} = \frac{1}{2}\overrightarrow {{\rm{A}}{{\rm{A}}^\prime }} = \frac{1}{2}\overrightarrow {\rm{a}} \), \(\overrightarrow {{\rm{AN}}} = \frac{1}{2}(\overrightarrow {{\rm{AC}}} + \overrightarrow {{\rm{AC}}} ) = \frac{1}{2}\overrightarrow {\rm{a}} + \overrightarrow {\rm{b}} \)
Vì G là trọng tamm của tam giác \({A^\prime }{B^\prime }{C^\prime }\) nên
\(\overrightarrow {{\rm{AG}}} = \frac{1}{3}\left( {\overrightarrow {{\rm{A}}{{\rm{A}}^\prime }} + \overrightarrow {{\rm{A}}{{\rm{B}}^\prime }} + \overrightarrow {{\rm{A}}{{\rm{C}}^\prime }} } \right) = \vec a + \frac{1}{3}\overrightarrow {\rm{b}} + \frac{1}{3}\overrightarrow {\rm{c}} \)
Ta có
\(\begin{array}{l}\overrightarrow {{\rm{MG}}} = \overrightarrow {{\rm{AG}}} – \overrightarrow {{\rm{AM}}} = \frac{1}{2}\overrightarrow {\rm{a}} + \frac{1}{3}\overrightarrow {\rm{b}} + \frac{1}{3}\overrightarrow {\rm{c}} \\ \Rightarrow \overrightarrow {{\rm{MG}}} = \frac{1}{2}\overrightarrow {{\rm{AB}}} + \frac{1}{3}\overrightarrow {{\rm{AN}}} \end{array}\)
suy ra \(\overrightarrow {{\rm{MG}}} ,{\overrightarrow {{\rm{AB}}} ^\prime },\overrightarrow {{\rm{AN}}} \) đồng phẳng,
Mặt khác \(G \notin \left( {{A^\prime }N} \right) \Rightarrow MG//\left( {{A^\prime }{B^\prime }N} \right)\)(1)
Tương tự
\[\begin{array}{l}\overrightarrow {{\rm{M}}{{\rm{C}}^\prime }} = \overrightarrow {{\rm{A}}{{\rm{C}}^\prime }} – \overrightarrow {{\rm{AM}}} = \overrightarrow {\rm{a}} + \overrightarrow {\rm{c}} – \frac{1}{2}\overrightarrow {\rm{u}} = \frac{1}{2}\overrightarrow {\rm{u}} + \overrightarrow {\rm{k}} = \overrightarrow {{\rm{AN}}} \\ \Rightarrow {\rm{M}}{{\rm{C}}^\prime }//\left( {{\rm{A}}{{\rm{B}}^\prime }{\rm{N}}} \right)(2)\end{array}\]
Từ \((1)\) và \((2)\) suy ra
\(\left\{ {\begin{array}{*{20}{l}}{MG//\left( {A{B^\prime }N} \right)}\\{M{C^\prime }\left( {A{B^\prime }N} \right)}\end{array} \Rightarrow \left( {MG{C^\prime }} \right)//\left( {A{B^\prime }N} \right)} \right.\).
Xem thêm