Chuyên đề Phép dời hình và phép đồng dạng trong mặt phẳng 2023 hay, chọn lọc

Chuyên đề Phép dời hình và phép đồng dạng trong mặt phẳng

Phần 1: Các bài toán về phép tịnh tiến và cách giải

I. Lý thuyết ngắn gọn

1.Trong mặt phẳng cho vectơ v→. Phép biến hình biến mỗi điểm M thành điểm M′ sao cho MM’→ = v→được gọi là phép tịnh tiến theo vectơ v→, ký hiệu T_v→ 

 

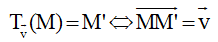
2.Trong mặt phẳng tọa độ Oxy, cho điểm M (x; y) và v→ = (a;b). Khi đó:  

3.Các tính chất của phép tịnh tiến:

-Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kỳ

– Phép tịnh tiến biến đường thẳng thành đường thằng song song hoặc trùng với nó, biến đoạn thằng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính

II. Các dạng toán phép tịnh tiến

Dạng 1: Xác định ảnh của một hình qua phép tịnh tiến

Phương pháp giải: Sử dụng định nghĩa và các tính chất hoặc biểu thức tọa độ của phép tịnh tiến

Ví dụ 1:Trong mặt phẳng tọa độ Oxy, cho v→ = (3;4). Hãy tìm ảnh của điểm A (1; -1) qua phép tịnh tiến theo vectơ v→. 

Lời giải

Gọi A′ (x′; y′) là ảnh của điểm A qua phép tịnh tiến theo vectơ v→ 

Áp dụng biểu thức tọa độ của phép tịnh tiến: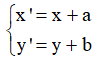  

Ta có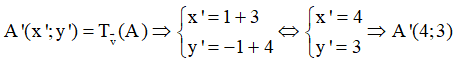  

Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho v→ = (2;-4) và đường thẳng d có phương trình 2x – 3y + 5 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến T_v→ 

Lời giải

Lấy điểm M (x; y) tùy ý thuộc d, ta có: 2x – 3y + 5 = 0       (1)

Gọi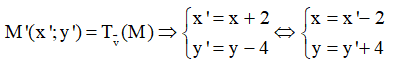  

Thay vào (1) ta được phương trình: 2(x^‘ – 2) – 3(y^‘ + 4) + 5 = 0 => 2x^‘ – 3y^‘ = 0 

Vậy ảnh của d là đường thẳng d’: 2x – 3y – 11 = 0

Dạng 2: Xác định phép tịnh tiến khi biết ảnh và tạo ảnh

Phương pháp giải: Xác định phép tịnh tiến tức là tìm tọa độ của v→. Để tìm tọa độ của v→, ta có thể giả sử v = (a; b), sử dụng các dữ kiện trong giả thiết của bài toán để thiết lập hệ phương trình hai ẩn a,b và giải hệ tìm a,b

Ví dụ 3: Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x + y – 9 = 0. Tìm phép tịnh tiến theo vectơ v→ có giá song song với Oy biến d thành d′ đi qua điểm A (2; 4)

Lời giải

Vì v→ có giá song song với Oy nên v→ = (0;k ) (k ≠ 0)

Lấy M(x;y) ∈ d => 3x + y – 9 = 0    (1) 

Gọi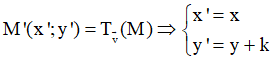  

Thay vào (1) ta được: 3x’ + y’ – k – 9 = 0

Do đó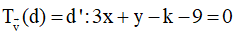  

Mà A (2; 4) thuộc d, suy ra k=1

Vậy v→ = (0;1) 

Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng d: 2x –3y + 3 = 0 và d′: 2x – 3y – 5 = 0. Tìm tọa độ v→ có phương vuông góc với d để T_v→(d) = d’ 

Lời giải

Gọi v→ = (a;b) 

Lấy điểm M (x; y) tùy ý thuộc d, ta có: d: 2x – 3y + 3 = 0   (1)

Gọi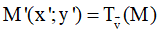  

Ta có: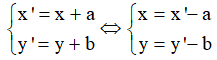  

Thay vào (1) được: 2x’ – 3y’ – 2a + 3b + 3 = 0

Suy ra: -2a + 3b + 3 = -5 ⇔ 2a – 3b = 8 Chuyển vế sai   

Vectơ pháp tuyến của đường thẳng d là n→ = (2;-3) suy ra vectơ chỉ phương của d là u→ = (3;2) 

Suy ra: v→.u→ = 3a + 2b = 0 

Có hệ phương trình: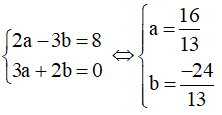   

Vậy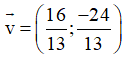  

Dạng 3: Dùng phép tịnh tiến để giải các bài toán dựng hình

Phương pháp giải: 

– Để dựng một điểm M ta tìm cách xem nó là ảnh của một điểm đã biết qua một phép tịnh tiến, hoặc xem M là giao điểm của hai đường trong đó một đường cố định còn một đường là ảnh của một đường đã biết qua phép tịnh tiến

– Sử dụng kết quả: Nếu 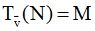 và N ∈ H thì N ∈ (H^‘) , trong đó 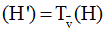và kết hợp với M thuộc hình (K) để suy ra M ∈ (H^‘) ∩ (K)

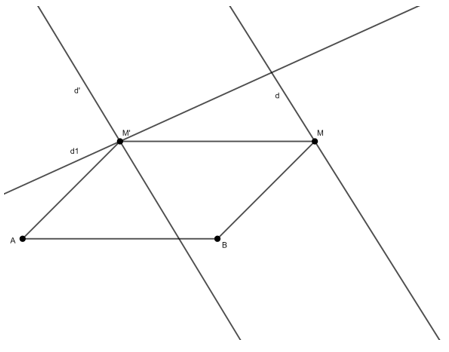
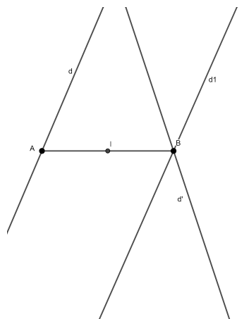
Ví dụ 5:  Trong mặt phẳng cho hai đường thẳng d và d1 cắt nhau và hai điểm A, B không thuộc hai đường thẳng đó sao cho đường thẳng AB không song song hoặc trùng với d (hay d1). Hãy tìm điểm M trên d và điểm M’ trên d1 để tứ giác ABMM’ là hình bình hành

Lời giải:

Điểm M’ là ảnh của điểm M qua phép tịnh tiến theo vectơ BA→. Khi đó điểm M’ vừa thuộc d1 vừa thuộc d’ là ảnh của d qua phép tịnh tiến theo vectơ BA→ 

Từ đó có thể suy ra cách dựng: 

-Dựng d’ là ảnh của d qua phép tịnh tiến theo vectơ BA→ 

-M’ là giao điểm của d’ và d1

-Dựng điểm M là ảnh của điểm M’ qua phép tịnh tiến theo vectơ BA→ 

Suy ra tứ giác ABMM’ chính là hình bình hành thoả mãn yêu cầu của đầu bài

Ví dụ 6: Cho tam giác ABC. Dựng đường thẳng d song song với BC, cắt hai cạnh AB, AC lần lượt tại M, N sao cho AM = CN

Lời giải

Cách dựng:

-Dựng phân giác trong AP của góc A

-Dựng đường thẳng đi qua P song song với AC cắt AB tại M

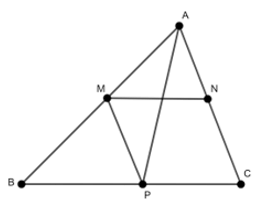
-Dựng ảnh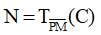  

Đường thẳng MN chính là đường thẳng thỏa yêu cầu bài toán

Dạng 4: Sử dụng phép tịnh tiến để giải bài toán tìm tập hợp điểm

Phương pháp giải: Nếu 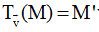 và điểm M di động trên hình (H) thì điểm M’ thuộc hình (H’), trong đó (H’) là ảnh của hình (H) qua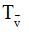  

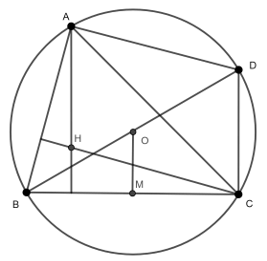
Ví dụ 7:  Cho hai điểm phân biệt B và C cố định trên đường tròn (O) tâm O, điểm A di động trên đường tròn (O). Chứng minh rằng khi A di động trên đường tròn (O) thì trực tâm của tam giác ABC di động trên một đường tròn

Lời giải

Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Tia BO cắt đường tròn ngoại tiếp tam giác ABC tại D

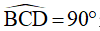 nên DC // AH

Tương tự AD // CH

Suy ra: ADCH là hình bình hành

 

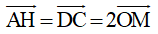
OM không đổi nên H là ảnh của A qua phép tịnh tiến theo vectơ 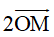.  Do đó khi điểm A di động trên đường tròn (O) thì H di động trên đường tròn (O‘) là ảnh của (O) qua phép tịnh tiến theo vectơ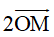  

Ví dụ 8: Cho tam giác ABC có đỉnh A cố định, 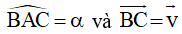 không đổi. Tìm tập hợp các điểm B, C

Lời giải

Gọi O là tâm đường tròn ngoại tiếp tam giác ABC
Khi đó theo định lí sin ta có 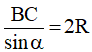  không đổi 

Vậy 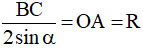 không đổi nên O di động trên đường tròn tâm A bán kính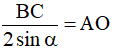  

Ta có OB = OC = R không đổi và 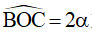 không đổi suy ra  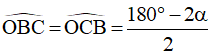không đổi

Mặt khác 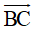có phương không đổi nên  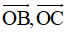cũng có phương không đổi

Đặt 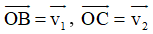 không đổi thì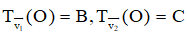  

Vậy tập hợp điểm B là đường tròn 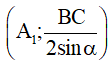 ảnh c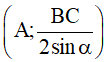ủa  qua 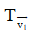và tập hợp điểm C là đường tròn  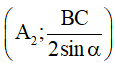ảnh c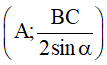ủa  qua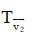  

III. Bài tập áp dụng

Bài 1: Cho hai điểm phân biệt B, C cố định trên đường tròn (O) tâm O. Điểm A di động trên (O). Chứng minh khi A di động trên (O) thì trực tâm của tam giác ABC di động trên một đường tròn

Bài 2: Trong mặt phẳng Oxỵ cho đường thẳng d có phương trình 3x – y – 9 = 0. Tìm phép tịnh tiến theo vectơ có phương song song với trục Ox biến d thành đường thẳng d’ đi qua gốc toạ độ và viết phương trình đường thẳng d’

Bài 3: Cho đoạn thẳng AB và đường tròn (C) tâm O, bán kính r nằm về một phía của đường thẳng AB. Lấy điểm M trên (C), rồi dựng hình bình hành ABMM’. Tìm tập hợp các điểm M’ khi M di động trên (C)

Bài 4: Trong mặt phẳng toạ độ Oxy cho ba điểm A (-1; -1), B (3; 1), C (2; 3). Xác định toạ độ điểm D sao cho tứ giác ABCD là hình bình hành

Bài 5: Trong mặt phẳng toạ độ Oxy cho đường tròn (C) có phương trình: x² + y² – 2x + 4y – 4 = 0. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ v→ = (-2;3) 

Bài 6: Cho hình bình hành ABCD. Dựng ảnh của tam giác ABC qua phép tịnh tiến theo vectơ AD→

Bài 7: Cho đường (O) với đường kính AB cố định, một đường kính MN thay đổi. Các đường thẳng AM, AN cắt tiếp tuyến tại B tại P và Q. Tìm quỹ tích trực tâm các tam giác MPQ và NPQ

Bài 8: Tam giác ABC cố định trực tâm H. Vẽ hình thoi BCDE. Từ D và E vẽ các đường vuông góc với AB và AC, các đường thẳng này cắt nhau tại M. Tìm tập hợp điểm M

Bài 9: Trong mặt phẳng với hệ tọa độ Oxy, cho hai parabol (P): y = x² và (Q): y = x² + 2x + 2  .Tìm phép tịnh tiến T biến (Q) thành (P)

Bài 10: Trong mặt phẳng tọa độ Oxy, cho parabol (P): y = x² + 2x + 1 . Viết phương trình (P’) sao cho qua phép tịnh tiến theo v→ = (1;1) thì (P) là ảnh của (P’)

Phần 2: Các bài toán về phép đối xứng tâm và cách giải

I. Lý thuyết ngắn gọn

1. Cho điểm I phép biến hình biến điểm I thành chính nó và biến mỗi điểm M khác I thành điểm M′ sao cho I là trung điểm của MM′ được gọi là phép đối xứng tâm I, kí hiệu D_I 

 

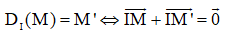
Nếu D_I ((H)) = (H) thì I được gọi là tâm đối xứng của hình H

2. Trong mặt phẳng Oxy cho I (a; b), M(x; y). Gọi M’ (x’; y’) là ảnh của M qua phép đối xứng tâm I thì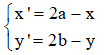  

3. Tính chất

– Phép đối xứng tâm bảo toàn khoảng cách giữa hai điểm bất kỳ

– Phép đối xứng tâm biến 3 điểm thẳng hàng thành 3 điểm thẳng hàng và không thay đổi thứ tự của chúng

– Phép đối xứng tâm I biến đường thẳng thành đường thẳng song song hoặc trùng với nó; biến đa giác thành đa giác bằng đa giác đã cho; biến đường tròn thành đường tròn có bán kính bằng bán kính đường tròn đã cho 

II. Các dạng toán phép đối xứng tâm

Dạng 1: Xác định ảnh của một hình qua phép đối xứng tâm

Phương pháp giải: Sử dụng biểu thức tọa độ và các tính chất của phép đối xứng tâm

Ví dụ 1: Cho điểm I(2; 2) và đường thẳng d: x + 5y + 1 = 0. Tìm ảnh của d qua phép đối xứng tâm I

Lời giải

Lấy điểm M(x,y) ∈ d => x + 5y + 1 = 0   (1)

Gọi M^‘(x^‘;y^‘) = D_I(M) thì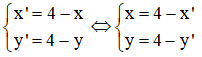   

Thay vào (1) được (4 – x^‘) + 5(4 – y^‘) + 1 = 0 => x^‘ + 5y^‘ – 25 = 0 

Vậy ảnh của d là đường thẳng d’: x + 5y – 25 = 0

Ví dụ 2: Trong mặt phẳng Oxy cho điểm A (-1; 3) và đường thẳng d có phương trình: x – 2y + 3 = 0 . Tìm ảnh của A và d qua phép đối xứng tâm O ( với O là gốc tọa độ)

Lời giải

Gọi A’ (x’; y’) là ảnh của A qua phép đối xứng tâm O (0; 0). Theo công thức tọa độ của phép đối xứng ta có

 

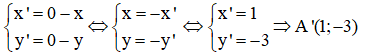
Gọi M (x; y) là một điểm bất kỳ thuộc d và M’ (x’; y’) là một điểm bất kỳ thuộc d’ là ảnh của d qua phép đối xứng tâm O. Theo công thức tọa độ của phép đối xứng ta có:

 

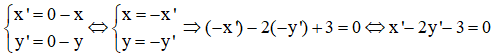
Do đó d’ có phương trình x – 2y – 3 = 0

Dạng 2: Xác định tâm đối xứng khi biết ảnh và tạo ảnh

Ví dụ 3: Trong mặt phẳng Oxy cho đường thẳng d: x – 2y + 2 = 0 và d’: x – 2y -8 = 0. Tìm phép đối xứng tâm biến d thành d’ và biến trục Ox thành chính nó 

Lời giải

Gọi M (x; y) thuộc d; M’ (x’; y’) thuộc d’, M’ là ảnh của M qua phép đối xứng tâm I. Giả sử tâm đối xứng là I (a; b), thì theo công thức có:

   

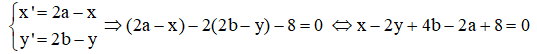
Để trục Ox thành chính nó thì tâm đối xứng phải có dạng: I (a; 0) tức b=0

Suy ra: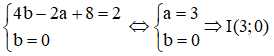   

Ví dụ 4: Cho đường thẳng d: x – 2y + 2 = 0 và d’: x – 2y – 8 = 0. Tìm phép đối xứng tâm biến d thành d’ và biến trục Oy thành chính nó

Lời giải

Giao của hai đường thẳng d : x – 2y + 2 = 0 và d ‘: x – 2y – 8 = 0 với trục Oy là A (0; 1), A’ (0; – 4)

Theo giả thiết biến d thành d’ và biến trục Oy thành chính nó thì A biến thành A’ nên tâm đối xứng là I trung điểm của AA’ là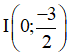  

Dạng 3: Tìm tâm đối xứng của một hình

Phương pháp giải: Điểm I được gọi là tâm đối xứng của hình H nếu phép đối xứng tâm I biến hình H thành chính nó. Khi đó ta nói H là hình có tâm đối xứng.

Ví dụ 5: Tìm tâm đối xứng biến điểm A (4; 3) thành điểm A’ (6; 1).

Lời giải

I (a; b) là trung điểm của AA^‘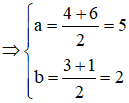 

Vậy tâm đối xứng cần tìm là I (5; 2)

Ví dụ 6: Tìm tâm đối xứng của đường cong (C) có phương trình: y = x³ – 3x² + 3 

Lời giải

Lấy điểm M(x,y) ∈ C => y = x³ – 3x² + 3  (1)

Gọi I (a; b) là tâm đối xứng của (C) và M’ (x’; y’) là ảnh của M qua phép đối xứng tâm I

Ta có: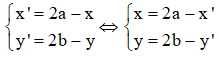  

Thay vào (1) được: 2b – y^‘ = (2a – x)³ – 3(2a – x)² + 3

⇔ y^‘ = x^‘3 – 3x^‘2 + 3 + (6 – 6a)x^‘2 + (12a² – 12a)x^‘ – 8a³ + 12a² + 2b – 6  (2)

Mặt khác M^‘ ∈ (C) nên y^‘ = x^‘3 – 3x^‘2 + 3 

Do đó (2) ⇔ (6 – 6a)x^‘2 + (12a² – 12a)x^‘ – 8a³ + 12a² + 2b – 6 = 0 

 

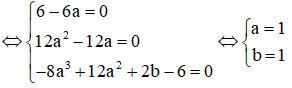
Vậy I (1; 1) là tâm đối xứng của (C)

Dạng 4: Sử dụng phép đối xứng tâm để giải các bài toán dựng hình

Phương pháp giải:  Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay D_I nào đó

Ví dụ 7: Cho hai đường thẳng d, d’ và điểm I. Tìm điểm A trên d và điểm B trên d’ sao cho I là trung điểm của đoạn thẳng AB

Lời giải

-Dựng đường thẳng d1 là ảnh của d qua phép đối xứng tâm I

-Dựng giao điểm B của d’ và d1

-Dựng A là giao điểm của đường thẳng BI và đường thẳng d

Số nghiệm hình là số giao điểm của đường thẳng d1 và d’

– Nếu d’ và d1 song song thì bài toán vô nghiệm 

-Nếu d’ và d1 cắt nhau thì bài toán có 1 nghiệm 

-Nếu d’ và d1 trùng nhau thì bài toán có vô số nghiệm

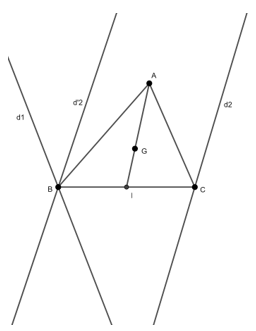
Ví dụ 8: Cho hai đường thẳng d1, d2 và hai điểm A, G không thuộc d1, d2. Hãy dựng tam giác ABC có trọng tâm G và hai đỉnh B, C lần lượt thuộc d1 và d2

Lời giải

Giả sử đã dựng được tam giác ABC thỏa mãn yêu cầu bài toán

Gọi I là trung điểm của BC thì D_I(C) = B 

C ∈ d2 nên B ∈ d’2 với d’2 là ảnh của d2 qua phép đối xứng tâm I

Ta lại có B ∈ d1 => B = d1 ∩ d’2 

Cách dựng:

-Dựng điểm I sao cho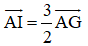  

-Dựng đường thẳng d’2 ảnh của d2 qua D_I 

-Gọi B = d1 ∩ d’2  

-Dựng điểm C = D_I(B) 

Tam giác ABC là tam giác phải dựng

Dạng 5: Sử dụng phép đối xứng tâm để giải bài toán tập hợp điểm

Phương pháp giải: Để tìm quỹ tích (tập hợp điểm), nếu có phép đối xứng tâm O biến điểm M thành M’ và (C) là tập hợp điểm của M thì ảnh (C’) qua tâm đối xứng tâm O là tập hợp của M’

Ví dụ 9: Cho trên đường tròn (O)  hai điểm cố định B, C và một điểm A thay đổi. Gọi H là trực tâm của tam giác ABC và H’ là điểm sao cho tứ giác BHCH’ là hình bình hành. Chứng minh rằng khi A thay đổi thì H’ luôn nằm trên đường tròn (O). Tìm tập hợp của H

Lời giải

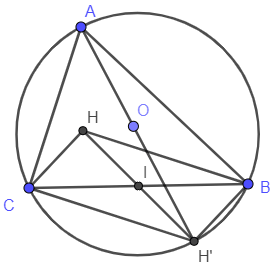
Gọi A’ là điểm xuyên tâm đối của A trên (O). Ta có:

A’B ⊥ AB ( ΔABA’ là tam giác có cạnh huyền là đường kính)

CH ⊥ AB (do CH là đường cao)

Nên AB // CH (1)

Tương tự ta chứng minh được A’C // BH (2)

(1) và (2) => BHCA’ là hình bình hành

=> Lấy H’ trung với A’. Vậy BHCH’ là hình bình hành và H’ luôn nằm trên đường tròn.

Trong hình bình hành BHCH’, có HH’ và BC là hai đường chéo nnen HH’ nhận trung điểm I của BC cố định làm trung điểm.

Do đó H là điểm đối xứng với H’ qua I.

Mà H’ ∈ (O) nên H ∈ một đường tròn đối xứng với (O) qua I

Ví dụ 10: Một hình bình hành ABCD có hai đỉnh A, C cố định, còn đỉnh B thay đổi trên đường thẳng d. Tìm quỹ tích đỉnh D

Lời giải

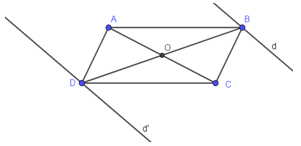
Vì ABCD là hình bình hành có hai đỉnh A, C cố định nên tâm O là trung điểm của đường chéo AC 

Suy ra: O cố định

Mà tâm O là trung điểm đường chéo BD. Do đó phép đối xứng tâm O biến B thành D

Mà B chạy trên đường thẳng d nên điểm D chạy trên đường thẳng d’ ảnh của d qua phép đối xứng tâm O

Ngược lại với mọi điểm D thuộc đường thẳng d’ ta luôn tìm được điểm B thuộc d sao cho O là trung điểm của BD

Vậy quỹ tích của các điểm D là đường thẳng d’ ảnh của d qua phép đối xứng tâm O

III. Bài tập áp dụng

Bài 1: Trong mặt phẳng hệ tọa độ Oxy, tìm tọa độ điểm M’ là ảnh của điểm M (2; 1) qua phép đối xứng tâm I (3; -2)

Bài 2: Một hình bình hành ABCD có hai đỉnh A, C cố định, còn đỉnh B thay đổi trên đường tròn (O; R) . Tìm quỹ tích của đỉnh D

Bài 3: Tìm tâm đối xứng của các hình sau đây: tam giác đều, hình bình hành, lục giác đều, đường tròn, hình gồm hai đường tròn bằng nhau

Bài 4: Cho đường tròn (O) và dây cung AB cố định, M là một điểm di động trên (O), M không trùng với A, B. Hai đường tròn (O1), (O2) cùng đi qua M và tiếp xúc với AB tại A và B. Gọi N là giao điểm thứ hai của (O1) và (O2). Tìm tập hợp điểm N khi M di động

Bài 5: Tìm tâm đối xứng biến điểm A (5; 0) thành điểm A’ (8; 8)

Bài 6: Cho hình bình hành MNPQ nội tiếp hình bình hành ABCD (4 đỉnh nằm trên bốn cạnh). Chứng minh hai hình bình hành có cùng tâm đối xứng

Bài 7: Xác định ảnh qua phép đối xứng tâm I (4; -7) của:

a. Điểm A (3; -2) của đường thẳng d: 3x – 6y + 1 = 0

b. Đường tròn x² + y² – 4x – 2y – 4 = 0 

Bài 8: Tìm ảnh qua phép đối xứng tâm I (-3; 5) của:

a. Điểm A (3; -4)

b. Đường thẳng d: 2x – y +1 = 0

Bài 9: Cho phép đối xứng tâm I (p; 3). Tìm ảnh của đồ thị hàm số (C): y = 2sin2x – 5

Bài 10: Giả sử phép đối xứng tâm D₀ biến đường thẳng d thành đường thẳng d’. Chứng minh nếu d không đi qua tâm đối xứng O thì d’ song song với d, O cách đều d và d’

Phần 3: Các bài toán về phép đối xứng trục và cách giải

I. Lý thuyết ngắn gọn

1. Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M′ sao cho d là đường trung trực của đoạn thẳng MM′ được gọi là phép đối xứng qua đường thẳng d, hay còn gọi là phép đối xứng trục d

Ký hiệu: D_d 

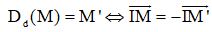 (Với I là gối đẻm của d với MM’)

2. D_d [(H)] = (H) thì d được gọi là trục đối xứng của hình (H)

3.Trong mặt phẳng Oxy với mỗi điểm M (x; y), gọi M^‘(x^‘;y^‘) = D_d(M)

Nếu d là trục Ox thì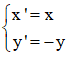  

Nếu d là trục Oy thì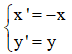  

4.Tính chất

– Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì

– Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn cùng bán kính

II. Các dạng toán phép đối xứng trục

Dạng 1: Xác định ảnh của một hình qua phép đối xứng trục

Phương pháp giải: Để xác định ảnh (H′) của hình (H) qua phép đối xứng trục ta có thể dùng một trong các cách sau:

– Dùng định nghĩa phép đối xứng trục

– Dùng biểu thức tọa độ của phép đối xứng trục mà trục đối xứng là các trục tọa độ Ox, Oy

– Dùng biểu thức vectơ của phép đối xứng trục

Ví dụ 1: Trong mặt phẳng Oxy cho A (1; -2) và B (3; 1). Tìm ảnh của A, B và đường thẳng AB qua phép đối xứng trục Ox

Lời giải

A’ là ảnh của A qua phép đối xứng qua trục Ox có tọa độ là A’ (1; 2)

B’ là ảnh của B qua phép đối xứng qua trục Ox có tọa độ là B’ (3; -1)

Ảnh của đường thẳng AB qua phép đối xứng qua trục Ox chính là đường thẳng A’B’ nên đường thẳng A’B’ có phương trình: 

 

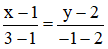
=> 3x + 2y – 7 = 0 

Ví dụ 2: Trong mặt phẳng Oxy có đường thẳng d có phương trình: 3x – y + 2 = 0. Viết phương trình đường thẳng d’ là ảnh của đường thẳng d qua phép đối xứng trục Oy

Lời giải

Gọi M (x; y) tùy ý thuộc d 

Suy ra: 3x – y + 2 = 0   (1)

  

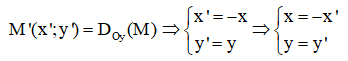
Thay vào (1) được: 3(-x^‘) – y^‘ + 2 = 0 ⇔ 3x^‘ + y^‘ – 2 = 0 

Vậy tọa độ M’ thỏa mãn phương trình d’: 3x + y – 2 = 0

Dạng 2: Dùng phép đối xứng trục để giải các bài toán dựng hình

Phương pháp giải: 

– Dựng điểm M: Tìm một hình (H) cố định và đường thẳng d cố định cho trước sao cho khi thực hiện phép đối xứng trục d ta có được ảnh là hình (H’) giao với (C) cố định tại điểm M cần dựng 

– Thực hiện các phép đối xứng trục d để tìm các điểm còn lại từ đó ta có hình cần dựng

Ví dụ 3: Dựng hình vuông ABCD biết hai đỉnh A và C nằm trên đường thẳng d₁ và hai đỉnh B, D lần lượt thuộc hai đường thẳng d₂,d₃ 

Lời giải

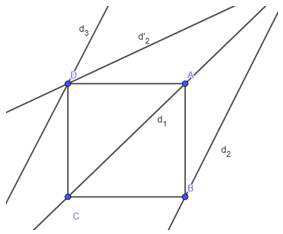
– Giả sử đã dựng được hình vuông ABCD thỏa điều kiện của bài toán

Do  và AC là trục đối xứng của hình vuông ABCD 

Mặt khác B ∈ d₂ nên D ∈ d^‘₂ trong đó d^‘₂ là đường thẳng đối xứng với d₂ qua  

Suy ra: D = d^‘₂ ∩ d₃  

– Cách dựng:

Dựng d^‘₂ = D_d1(d₂), gọi D = d₃ ∩ d^‘₂ 

Dựng đường thẳng qua D vuông góc với d₁ tại O và cắt d₂ tại B

Dựng đường tròn tâm O đường kính BD cắt  tại A, C (A, C theo thứ tự để tạo thành tứ giác ABCD)

– Nhận xét:

TH1: d₂ cắt d₃ khi đó:

Nếu d^‘₂ ∩ d₃ thì bài toán có 1 nghiệm hình

Nếu d^‘₂ // d₃ thì bài toán có vô nghiệm hình

TH2: d₂ // d₃. Khi đó

Nếu d₁ song song và cách đều d₂ và d₃ thì bài toán có vô số nghiệm hình

Nếu d₁ hợp với d₂ và d₃ một góc 45 thì bài toán có 1 nghiệm hình

Nếu d₁ song song và không cách đều d₂, d₃ hoặc d₁ không hợp với d₂, d₃ một góc 45 thì bài toán vô nghiệm hình

Ví dụ 4: Cho hai đường tròn (C), (C′) có bán kính khác nhau và đường thẳng d. Hãy dựng hình vuông ABCD có hai đỉnh A, C lần lượt nằm trên (C), (C′) và hai đỉnh còn lại nằm trên d

Lời giải

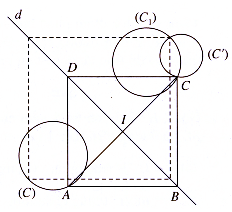
– Dựng đường tròn (C₁) là ảnh của (C) qua D_d 

– Gọi C là giao điểm của (C₁) và (C’) 

– Dựng điểm A đối xứng với C qua d

– Gọi I = AC ∩ d 

Lấy trên d hai điểm B, D sao cho: IB = ID = IA

Khi đó ABCD là hình vuông cần dựng

– Số nghiệm hình bằng số giao điểm của (C₁) và (C’)

Dạng 3: Dùng phép đối xứng trục để giải các bài tập hợp điểm 

Phương pháp giải: 

– Tìm quỹ tích điểm M: Từ giả thiết chọn điểm E di động sao cho EM nhận đường thẳng d cố định làm trục đối xứng

– Xác định hình (H) là quỹ tích của E

– Khi đó tập hợp các điểm M là (H’) – ảnh của (H) qua phép đối xứng trục d

Ví dụ 5: Cho A, B, C thuộc đường thẳng xx’ (B nằm giữa A và C). Một đường thẳng yy^‘ ⊥ xx^‘ tại C. Qua điểm A dựng đường thẳng di động Δ cắt yy’ tại M. Qua B dựng đường vuông góc với Δ cắt yy’ tại N. Chứng minh khi Δ quay quanh A thì đường tròn ngoại tiếp tam giác BMN còn đi qua một điểm cố định thứ hai

Lời giải

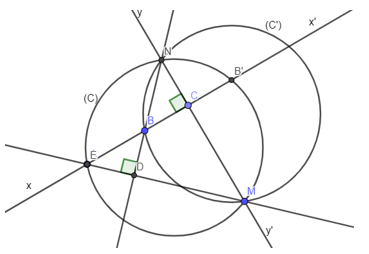
Gọi (C) là đường tròn ngoại tiếp tam giác AMN:

BN ⊥ AM 

AC ⊥ MN

Nên suy ra B là trực tâm của tam giác AMN

Gọi B’ là giao điểm của xx’ và đường tròn (C)

Dễ chứng minh được yy’ là trục đối xứng của BB’

Do đó B thuộc đường tròn (C^‘) = D_yy’ [(C)]

Vậy B^‘ ∈ (C) = D_yy’ [(C^‘)] 

Ví dụ 6: Cho tam giác ABC có hai đỉnh B, C di động trên đường thẳng cố định Δ Biết rằng trực tâm H của tam giác cố định và đường tròn ngoại tiếp tam giác ABC luôn đi qua một điểm cố định P khác H. Gọi O là tâm đường tròn ngoại tiếp tam giác ABC. Tìm quỹ tích điểm O

Lời giải

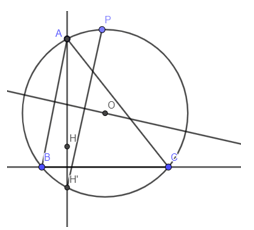
Gọi H^‘ = D_Δ(H) 

Suy ra H’ cố định và thuộc đường tròn (O)

Do đó O cách đều hai điểm cố định P và H’

Suy ra O thuộc đường trung trực PH’

III. Bài tập áp dụng

Bài 1: Trong mặt phẳng Oxy cho (P): y² = x. Hỏi parabol nào sau đây là ảnh của (P) qua phép đối xứng trục Oy

A. y² = x  

B. y² = -x 

C. x² = y 

D. x² = -y 

Bài 2: Trong mặt phẳng Oxy, qua phép đối xứng trục Oy. Điểm A (3; 5) biến thành điểm nào trong các điểm sau:

A. (3; 5)

B. (-3; 5)

C. (3; -5)

D. (-3; -5)

Bài 3: Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình (H). Hỏi (H) có mấy trục đối xứng?

A. 0

B. 1

C. 2

D. 3

Bài 4: Hình gồm hai đường thẳng d và d’ vuông góc với nhau có mấy trục đối xứng?

A. 0

B. 2

C. 4

D. Vô số

Bài 5: Cho đường tròn (C): x² + y² – 6x + 2y + 1 = 0. Tìm phương trình đường tròn đối xứng với (C) qua đường thẳng d: x – y = 0  

Bài 6: Trong mặt phẳng Oxy cho hai đường thẳng d: x – 5y + 7 = 0 và d’: 5x – y – 13 = 0. Tìm phép đối xứng qua trục biến d thành d’

Bài 7: Cho tam giác ABC vuông tại A, đường cao AH. Về phía ngoài tam giác dựng hai hình vuông ABDE và ACFG. Chứng minh AH, CD, BF đồng quy

Bài 8: Cho hình vuông ABCD và AB’C’D’ có các cạnh đều bằng a và cạnh A chung. Chứng minh có thể thực hiện một phép đối xứng trục biến hình vuông ABCD thành AB’C’D’

Bài 9: Cho tam giác ABC và đường thẳng d không đi qua A nhưng không qua B, C. Tìm ảnh của tam giác ABC qua phép đối xứng D_d 

Bài 10: Cho tam giác ABC có tâm đường tròn nội tiếp I, P là một điểm nằm trong tam giác. Gọi A′, B′, C′ là các điểm đối xứng với P lần lượt đối xứng qua IA, IB, IC. Chứng minh các đường thẳng AA′, BB′, CC′ đồng quy.

Phần 4: Các bài toán về phép quay và cách giải

I. Lý thuyết ngắn gọn

1. Cho điểm O và góc lượng giác α. Phép biến hình biến O thành chính nó và biến mỗi điểm M khác O thành điểm M′ sao cho OM′ = OM và góc lượng giác (OM;OM^‘) = α được gọi là phép quay tâm O, α được gọi là góc quay

Kí hiệu: Q_(O;α)             

Khi α = 2kπ, k ∈ Z thì Q_(O;α) là phép đồng nhất

Khi α = (2k+ 1)π, k ∈ Z thì Q_(O;α)  là phép đối xứng tâm O

2. Trong mặt phẳng Oxy, giả sử M (x; y) và M^‘(x^‘,y^‘) = Q_(O;α) (M) thì  

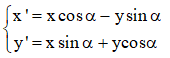
Trong mặt phẳng Oxy, giả sử M (x; y) và I (a; b) và M^‘(x^‘,y^‘) = Q_(O;α) (M) thì 

 

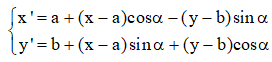
3. Các tính chất của phép quay:
– Bảo toàn khoảng cách giữa hai điểm bất kì
– Biến một đường thẳng thành đường thẳng
– Biến một đoạn thẳng thành đoạn thẳng bằng đoạn đã cho
– Biến một tam giác thành tam giác bằng tam giác đã cho
– Biến đường tròn thành đường tròn có cùng bán kính

II. Các dạng toán về phép quay

Dạng 1: Xác định ảnh của một hình qua phép quay
 Phương pháp giải: Sử dụng định nghĩa phép quay, biểu thức tọa độ của phép quay và các tính chất của phép quay

Ví dụ 1: Tìm ảnh của điểm A (3; 4) qua phép quay tâm O góc quay 90⁰ 

Lời giải

Với phép quay tâm O góc 90 độ điểm A thành A’(x; y) có tọa độ thỏa mãn:

 

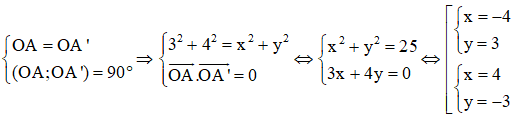
Do α = 90⁰ > 0 phép quay theo chiều dương suy ra: A’ (-4; 3)

Ví dụ 2: Trong mặt phẳng Oxy cho điểm M (2; 0) và đường thẳng d: x + 2y – 2 = 0. Xét phép quay Q tâm O góc quay 90⁰   

a. Tìm ảnh của điểm M qua phép quay Q
b. Tìm ảnh của d qua phép quay Q

Lời giải

a. Ta có vì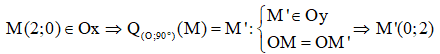  

b. Ta có M(2;0) ∈ d, ảnh của M qua phép quay Q theo câu a là M’ (0; 2)

Gọi d’ là ảnh của d qua Q ta có d’ là đường thẳng qua M’ và vuông góc với d

Đường thẳng d có VTPT là 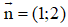 suy ra d’ có VTPT là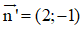  

Vậy phương trình của d’ là: 2(x – 0) – 1(y – 2) = 0 ⇔ 2x – y + 2 = 0 

Dạng 2: Sử dụng phép quay để giải các bài toán dựng hình

Phương pháp giải: Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay Q_(I;α) nào đó

Ví dụ 3: Cho hai đường thẳng a, b và điểm C không nằm trên chúng. Hãy tìm trên a và b lần lượt hai điểm A và B sao cho tam giác ABC là tam giác đều

Lời giải

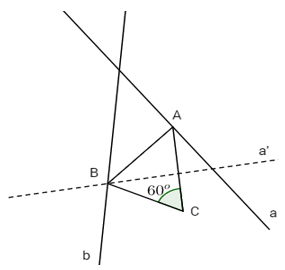
Nếu xem B là ảnh của A qua phép quay tâm C góc quay 60° thì B sẽ là giao của đường thẳng b với đường thẳng a’ là ảnh của a qua phép quay nói trên

Số nghiệm của bài toán là số giao điểm của đường thẳng b với đường thẳng a’

Ví dụ 4: Cho điểm A và hai đường thẳng d₁,d₂. Dựng tam giác ABC vuông cân tại A sao cho B ∈ d₁, C ∈ d₂ 

Lời giải

– Dựng đường thẳng d^‘₂ là ảnh của d₂ qua Q_(A;-90⁰) 

– Dựng giao điểm B = d₁ ∩ d^‘₂ 

– Dựng đường thẳng qua A vuông góc với AB cắt d₂ tại C

Tam giác ABC là tam giác cần dựng

Nhận xét:

– Nếu d₁,d₂ không vuông góc thì bài toán có một nghiệm hình

– Nếu d₁ ⊥ d₂ và A nằm trên đường phân giác của một trong các góc tạo bởi d₁,d₂ thì bài toán có vô số nghiệm hình

– Nếu d₁ ⊥ d₂ và A không nằm trên đường phân giác của một trong các góc tạo bởi d₁,d₂ thì bài toán vô nghiệm hình

Dạng 3: Sử dụng phép quay để giải các bài toán tập hợp điểm

Phương pháp giải: Xem điểm cần dựng là giao của một đường có sẵn và ảnh của một đường khác qua phép quay Q_(I;α) nào đó. Để tìm tập hợp điểm M′ ta đi tìm tập hợp điểm M mà Q_(I;α) nào đó biến điểm M thành điểm M′, khi đó nếu M ∈ (H) thì (M^‘) ∈ (H^‘) = Q_(I;α)((H))

Ví dụ 5: Cho đường tròn (O, R), A là một điểm cố định không trùng với tâm O, BC là một dây cung của (O), BC di động nhưng số đo của cung BC luôn bằng 120⁰.Gọi I là trung điểm của BC, vẽ tam giác đều AIJ. Tìm tập hợp điểm J

Lời giải

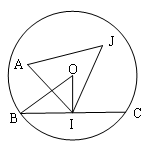
Ta có I là trung điểm của BC và cung BC = 120⁰ 

Nên OI ⊥ BC và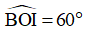  

Xét tam giác OIB có:

 

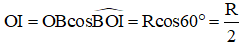
Do đó tập hợp các điểm I là đường tròn (γ)  tâm O bán kính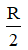  

Mặt khác, tam giác AIJ đều nên ta có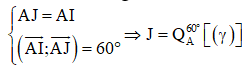
  

Mà tập hợp các điểm I là đường tròn (γ) nên tập hợp các điểm J là hai đường tròn (γ₁) và (γ₂) với:

 

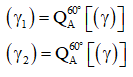
(γ₁) là đường tròn tâm (O₁) , bán kính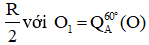 

(γ₂) là đường tròn tâm (O₂) , bán kính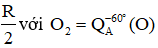 

Ví dụ 6: Cho đường thẳng a và một điểm G không nằm trên a. Với mỗi điểm A nằm trên a ta dựng tam giác đều ABC có tâm G. Tìm quỹ tích các điểm B, C khi A di động trên a

Lời giải

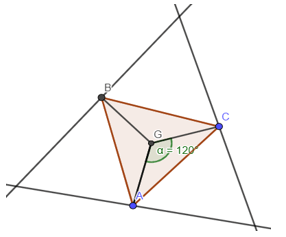
Do tam giác ABC đều và có tâm G nên phép quay tâm G góc quay 120⁰ biến A thành B hoặc C và phép quay tâm G góc quay 240⁰ biến A thành B hoặc C

Mà A ∈ a nên B, C thuộc các đường thẳng là ảnh của a trong hai phép quay nói trên

Vậy quỹ tích các điểm B, C là các đường thẳng ảnh của a trong hai phép quay tâm G góc quay 120⁰ và 240⁰ 

Dạng 4: Sử dụng phép quay để giải các bài toán hình học phẳng

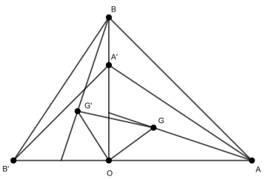
Ví dụ 7: Cho hai tam giác vuông cân OAB và OA’B’ có chung đỉnh O sao cho O nằm trên đoạn thẳng AB’ và nằm ngoài đoạn thẳng A’B. Gọi G và G’ lần lượt là trọng tâm các tam giác OAA’ và OBB’. Chứng minh rằng GOG’ là tam giác vuông cân

Lời giải

Xét phép quay Q tâm O góc quay 90⁰, ta có:

 

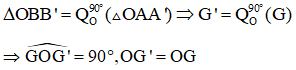
Vậy, ta được tam giác GOG’ là tam giác vuông cân

Ví dụ 8: Cho tam giác ABC, dựng ở ngoài tam giác ấy hai hình vuông ABDE và BCKF. Gọi P là trung điểm cạnh AC, H là điểm đối xứng của D qua B, M là trung điểm đoạn FH

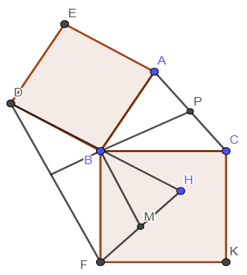
a. Xác định ảnh của hai vectơ 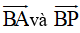 trong phép quay tâm B góc 90⁰ 

b. Chứng minh rằng DF = 2BP và DF vuông góc với BP

Lời giải

a. Ta có: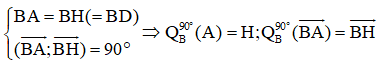   

 

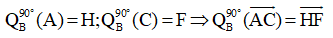
b. Vì P là trung điểm của AC nên theo tính chất của phép quay ta có ảnh của P qua phép quay trên trung điểm M của HF

 

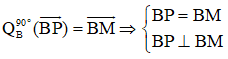
Mặt khác: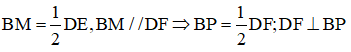  

III. Bài tập áp dụng

Bài 1:  Cho tam giác ABC vuông tại A. Về phía ngoài tam giác ta dựng các hình vuông ABDE và ACFH. Gọi I là trung điểm của cạnh BCE

a. Chứng minh rằng AE = CD

b. Gọi I, J lần lượt là trung điểm của AE và CD. Chứng minh rằng tam giác BIJ là một tam giác đều

Bài 2: Cho nửa đường tròn tâm O đường kính BC. Điểm A chạy trên nửa đường tròn đó. Dựng về phía ngoài của tam giác ABC hình vuông ABEF. Chứng minh rằng E chạy trên một nửa đường tròn cố định

Bài 3: Trong mặt phẳng toạ độ Oxy cho điểm A (3; 4). Hãy tìm toạ độ điểm A’ là ảnh của A qua phép quay tâm O góc 90⁰ 

Bài 4:  Cho hình vuông ABCD tâm O. M là trung điểm của AB, N là trung điểm của OA. Tìm ảnh của tam giác AMN qua phép quay tâm O góc 90⁰

Bài 5: Cho tam giác ABC. Dựng về phía ngoài của tam giác các hình vuông BCIJ, ACMN, ABEF và gọi O, P, Q lần lượt là tâm đối xứng của chúng

a. Gọi D là trung điểm của AB. Chứng minh rằng DOP là tam giác vuông cân đỉnh D

b. Chứng minh AO vuông góc với PQ và AO = PQ

Bài 6: Dựng tam giác đều biết ba đỉnh nằm trên bốn cạnh của một hình bình hành cho trước

Bài 7: Trong mặt phẳng Oxy, cho điểm B (-3; 6). Tìm tọa độ điểm E sao cho B là ảnh của E qua phép quay tâm O góc quay -90⁰ 

Bài 8: Cho hình vuông tâm O. Hỏi có bao nhiêu phép quay tâm O góc quay α, 0 < α ≤ 2π biến hình vuông trên thành chính nó?

A. 1

B. 2

C. 3

D. 4

Bài 9: Trong mặt phẳng với hệ trục tọa độ Oxy, cho điểm M (2; 0) và điểm N (0; 2). Phép quay tâm O biến điểm M thành điển N, khi đó góc quay của nó là bao nhiêu?
Bài 10: Trong mặt phẳng Oxy cho điểm A (3; 0). Tìm tọa độ ảnh A’ của điểm A qua phép quay Q₀⁹⁰⁰ 

Phần 5: Các bài toán về phép vị tự và cách giải

I. Lý thuyết ngắn gọn

– Cho điểm I và một số thực và k ≠ 0, phép biến hình biến mỗi điểm M thành điểm M′ sao cho 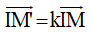 được gọi là phép vị tự tâm I, tỉ số k

Kí hiệu: v_(I;k) 

 

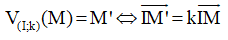
– Trong mặt phẳng tọa độ Oxy, cho I(x₀;y₀), M(x;y) gọi M^‘(x^‘;y^‘) = V_(I,k)thì  

– Nếu V_(I,k)(M) = M^‘; V_(I,k)(N)  = N^‘ thì 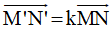 và M^‘N^‘ = |k|MN 

– Phép vị tự tỉ số k:

+ Biến ba điểm thẳng hàng thành ba điểm và bảo toàn thứ tự giữa ba điểm đó

+ Biến một đường thẳng thành đường thẳng song song hoặc trùng với đường thẳng đã cho, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng

+ Biến một tam giác thành tam giác đồng dạng với tam giác đã cho, biến góc thành góc bằng góc đã cho

+ Biến đường tròn có bán kính R thành đường tròn có bán kính |k|R 

– Tâm vị tự của hai đường tròn:

+ Với hai đường tròn bất kì luôn có một phép vị tự biến đường tròn này thành đường tròn kia, tâm của phép vị tự này được gọi là tâm vị tự của hai đường tròn

Cho hai đường tròn (I; R) và (I’; R’)

+ Nếu I ≡ I^‘  thì các phép vị tự 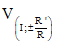 biến (I;R) thành (I’;R’)

+ Nếu I ≠ I^‘ và R ≠ R^‘ thì các phép vị tự 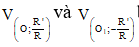 biến (I;R) thành (I’;R’). Ta gọi O là tâm vị tự ngoài còn O₁ là tâm vị tự trong của hai đường tròn

+ Nếu I ≠ I^‘ và R = R’ thì có V_(O1;-1)  biến (I;R) thành (I’;R’)

II. Các dạng toán phép vị tự

Dạng 1: Xác định ảnh của một hình qua phép vị tự

Phương pháp giải: Dùng định nghĩa, tính chất và biểu thức tọa độ của phép vị tự

Ví dụ 1: Cho điểm A (1; 2) và điểm I (2; 3). Tìm tọa độ A’ là ảnh của điểm A qua phép vị tự tâm I tỉ số 2

Lời giải

Gọi A’ (x’;y’) suy ra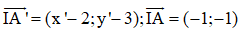  

Vì A’ là ảnh của điểm A qua phép vị tự tâm I tỉ số k=2 nên ta có: 

 

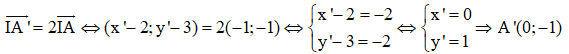
Ví dụ 2: Cho điểm M (-2; 5) và điểm E (2; -1). Tìm tọa độ điểm M’ là ảnh của điểm M qua phép vị tự tâm E tỉ số -2

Lời giải

Gọi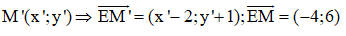  

Vì M’ là ảnh của điểm M qua phép vị tự tâm E tỉ số k = 2 nên ta có:

 

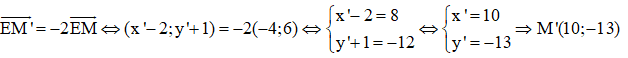
Dạng 2: Tìm tâm vị tự của hai đường tròn

Phương pháp giải: Sử dụng phương pháp tìm tâm vị tự của hai đường tròn

Ví dụ 3: Cho đường tròn (C) có phương trình (x – 2)² + (y + 3)² = 9 và đường tròn (C’) có phương trình x² + y² – 2x – 8y + 1 = 0. Tìm tọa độ tâm vị tự biến đường tròn (C) thành đường tròn (C’) biết tỉ số vị tự bằng 2

Lời giải

Đường tròn (C) có tâm là A (2; -3) bán kính R = 3

Đường tròn (C’) có tâm là A’ (1; 4) bán kính R’ = 4

Hai đường tròn (C) và (C’) có tâm không trùng nhau, bán kính khác nhau. Do đó tồn tại hai phép vị tự tâm I₁ tỉ số k = 2 và tâm I₂ tỉ số k = -2 biến đường tròn (C) thành đường tròn (C’)

TH1: Xét k = 2

Gọi I₁(x;y) là tâm vị tự, ta có: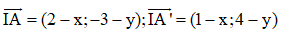  

 

 

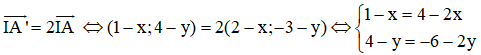
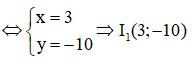
Do đó với k = 2 ta có một tâm vị tự ngoài là I₁(3,-10) 

TH2: Xét k = -2

Gọi I₂(x;y) là tâm vị tự ta có: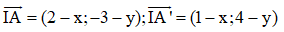  

Ta có: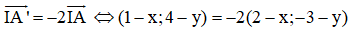   

 

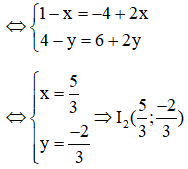
Do đó với k = -2 ta có một tâm vị tự trong là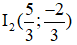  

Ví dụ 4:  Cho hai đường tròn (C): (x – 2)² + (y – 1)² = 4 và (C^‘): (x – 8)² + (y – 4)² = 16. Tìm tâm vị tự của hai đường tròn

Lời giải

Ta có: Đường tròn (C) có tâm I (2; 1) bán kính R = 2, đường tròn (C’) có tâm I’ (8; 4) bán kính R’ = 4

Do I ≠ I^‘; R ≠ R^‘nên có hai phép vị tự V_(J;2) và V_(J;-2) biến (C) thành (C’)

Gọi J (x; y)

Với k = 2 ta có: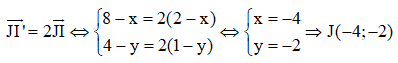  

Tương tự với k = -2 ta được J’ (4; 2)

Dạng 3: Sử dụng phép vị tự để giải các bài toán dựng hình

Phương pháp giải: Để dựng một hình (H) nào đó ta quy về dựng một số điểm (đủ để xác định hình (H)) khi đó ta xem các điểm cần dựng đó là giao của hai đường trong đó một đường có sẵn và một đường là ảnh vị tự của một đường khác

Ví dụ 5: Cho nửa đường tròn đường kính AB. Hãy dựng hình vuông có hai đỉnh nằm trên nửa đường tròn, hai đỉnh còn lại nằm trên đường kính AB của nửa đường tròn đó

Lời giải

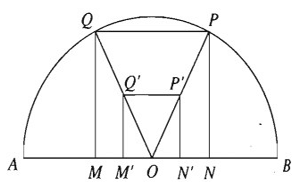
– Phân tích

Giả sử hình vuông MNPQ đã dựng xong thỏa mãn yêu cầu bài toán (với M, N nằm trên AB, còn P,Q nằm trên nửa đường tròn)

Gọi O là trung điểm của AB. Nối OQ và OP, dựng hình vuông M’N’P’Q’ sao cho M’, N’ nằm trên AB và O là trung điểm của M’N’ . Khi đó ta có: 

 

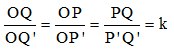
Ta xem như MNPQ là ảnh của M’N’P’Q’ qua phép vị tự tâm O tỉ số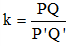  

– Cách dựng:

Dựng hình vuông M’N’P’Q’ ( có M’N’ thuộc AB và O là trung điểm của M’N’)

Nối OP’ và OQ’. Chúng cắt (O, AB) tại P và Q

Hình chiếu của P và Q trên AB là N và M. Khi đó MNPQ chính là hình vuông cần dựng

Dạng 4: Sử dụng phép vị tự để giải các bài toán tìm tập hợp điểm

Phương pháp giải: Để tìm tập hợp điểm M ta có thể quy về tìm tập hợp điểm N và tìm một phép vị tự V_(J;K) nào đó sao cho V_(J;K)(N) = M. Suy ra quỹ tích điểm M là ảnh của quỹ tích N qua V_(J;K)

Ví dụ 6: Cho đường tròn (O; R) và một điểm I nằm ngoài đường tròn sao cho OI = 3R, A là một điểm thay đổi trên đường tròn (O; R). Phân giác trong góc 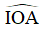 cắt IA tại điểm M. Tìm tập hợp điểm M khi A di động trên (O; R)

Lời giải

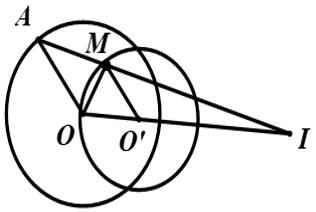
Theo tính chất đường phân giác ta có:  

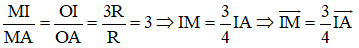
Suy ra 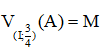 mà A thuộc đường tròn (O; R) nên M thuộc  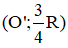ảnh của (O; R) qua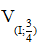 

Vậy tập hợp điểm M là 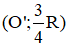 ảnh của (O; R) qua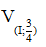 

Ví dụ 7: Cho tam giác ABC. Qua điểm M trên cạnh AB vẽ các đường song song với các đường trung tuyến AE và BF, tương ứng cắt BC và CA tai P, Q. Tìm tập hợp điểm R sao cho MPRQ là hình bình hành

Lời giải

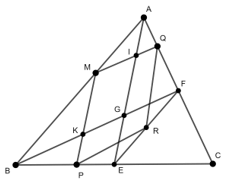
Gọi I = MQ ∩ AE, K = MP ∩ BF và G là trọng tâm của tam giác ABC

 

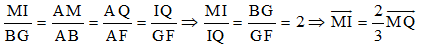
Tương tự ta có: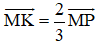  

Suy ra: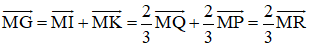  

Do đó: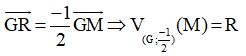  

Mà M thuộc cạnh AB nên R thuộc ảnh của cạnh AB qua 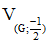 đoạn chính là đoạn EF

Vậy tập hợp điểm R là đoạn EF

III. Bài tập áp dụng

Bài 1: Trong mặt phẳng toạ độ Oxỵ cho đường tròn (C) có phương trình (x – 3)² + (y + 1)² = 9 

Hãy viết phương trình của đường tròn (C’) là ảnh của (C) qua phép vị tự tâm I (1; 2) tỉ số k = -2

Bài 2: Trong mặt phẳng toạ độ Oxy cho đường thẳng d có phương trình 2x + y – 4 = 0. Hãy viết phương trình của đường thẳng d₁ là ảnh của d qua phép vị tự tâm O tỉ số k = 3

Bài 3: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A (có bán kính khác nhau). Một điểm M nằm trên đường tròn (O). Dựng đường tròn đi qua M và tiếp xúc với O và O’

Bài 4: Gọi A là giao hai đường đường tròn cắt nhau O và O’ Hãy dựng qua A một đường thẳng cắt hai đường tròn tại B và C sao cho AC = 2AB

Bài 5: Cho đường tròn (O; R). Có bao nhiêu phép vị tự biến (O; R) thành chính nó?

A. 0

B. 1

C. 2

D. Vô số

Bài 6: Có bao nhiêu phép vị tự biến đường tròn (O; R) thành đường tròn (O’; R’) với R ≠ R^‘ ?

A. 0

B. 1

C. 2

D. Vô số

Bài 7: Có hai đường thẳng song song d và d’. Có bao nhiêu phép vị tự với tỉ số k = 20 biến đường thẳng d thành đường thẳng d’?

A. 0

B. 1

C. 2

D. Vô số

Bài 8: Có hai đường thẳng song song d và d’ và một điểm O không nằm trên chúng. Có bao nhiêu phép vị tự tâm O biến đường thẳng d thành đường thẳng d’?

A. 0

B. 1

C. 2

D. Vô số

Bài 9: Cho hình thang ABCD với hai cạnh đáy AB và CD thỏa mãn AB = 3CD. Phép vị tự biến điểm A thành điểm C và biến điểm B thành điểm D có tỉ số k là?

A. 3

B. -3

C.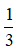  

D. –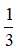 

Bài 10: Một hình vuông có diện tích bằng 4. Qua phép vị tự  thì ảnh của hình vuông trên có diện tích tăng gấp mấy lần diện tích ban đầu?

A.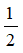  

B. 2

C. 4

D. 8

Phần 6: Các bài toán về phép đồng dạng và cách giải

I. Lý thuyết ngắn gọn

1. Phép biến hình F gọi là phép đồng dạng tỉ số k (k > 0) nếu với hai điểm M, N bất kì và ảnh M’; N’ của chúng ta có:

 

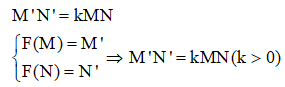
2. Nhận xét:

– Phép dời hình là phép đồng dạng tỉ số k = 1

– Phép vị tự V_(I;k) là phép đồng dạng tỉ số |k|  

– Nếu thực hiện liên tiếp phép đồng dạng tỉ số k và phép đồng dạng tỉ số p ta được phép đồng dạng tỉ số pk

– Phép đồng dạng tỉ số k là hợp thành của một phép dời hình và một phép vị tự tỉ số k hoặc – k. Nó cũng là hợp thành của một phép vị tự tỉ số k hoặc – k và một phép dời hình

3. Phép đồng dạng tỉ số k có các tính chất sau:

– Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữ các điểm ấy

–  Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng có độ dài bằng a thành đoạn thẳng có độ dài bằng ka

– Biến tam giác thành tam giác đồng dạng với tỉ số đồng dạng là k, biến góc thành góc bằng nó

– Biến đường tròn bán kính R thành đường tròn bán kính kR

4. Hai hình đồng dạng

Hai hình được gọi là đồng dạng với nhau nếu có một phép đồng dạng biến hình này thành hình kia

II. Các dạng bài về phép đồng dạng

Dạng 1: Xác định ảnh của một hình qua một phép đồng dạng

Phương pháp giải: Dùng định nghĩa và tính chất của phép đồng dạng

Ví dụ 1: Trong mặt phẳng Oxy cho đường thẳng d có phương trình x + y – 2 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm I (-1; -1) tỉ số 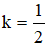 và phép quay tâm O góc -45 độ

Lời giải

Gọi  là ảnh của d qua phép vị tự tâm I (-1; -1) tỉ số 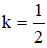. Vì song song hoặc trùng với d nên phương trình của nó có dạng x + y + c = 0

Lấy M(1;1) ∈ d  

 

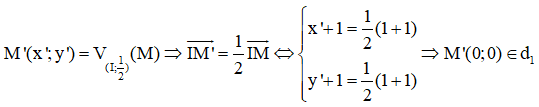
Vậy phương trình của d₁: x + y = 0 

Ảnh của d₁ qua phép quay tâm O góc -45 độ là đường thẳng Oy. Vậy phương trình d^‘: x = 0 

Ví dụ 2: Cho đường thẳng d: x – y + 1 = 0. Viết phương trình d’ là ảnh của đường thẳng d qua phép đồng dạng bằng cách thực hiện qua phép vị tự tâm I (1; 1), tỉ số k = 2 và phép tịnh tiến theo vectơ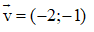  

Giải

Ta có M(0;1) ∈ d  

Qua phép vị tự tâm I, tỉ số k = 2 ta có: V_(I;2)(d) = d₁ 

Suy ra phương trình d₁ có dạng x – y + c = 0

Mặt khác: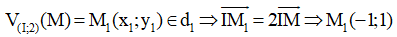  

Vậy d₁: x – y + 2 = 0 

Qua phép tịnh tiến theo vectơ 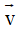 ta có: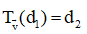  

Suy ra phương trình d₂ có dạng: x – y + d = 0

 

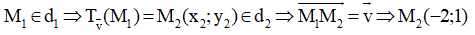
Vậy d₂ có phương trình x – y + 3 = 0

Qua phép đồng dạng đường thẳng d: x – y + 1 = 0 trở thành đường thẳng d₂: x – y + 3 = 0 

Dạng 2: Tìm phép đổng dạng biến hình H thành hình H’

Phương pháp giải: Tìm cách biểu thị phép đồng dạng đó như là kết quả của việc thực hiện liên tiếp các phép biến hình quen biết

Ví dụ 3: Cho hình chữ nhật ABCD. Gọi O là tâm đối xứng của nó. Gọi I, F, J, E lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tìm ảnh của tam giác AEO qua phép đồng dạng có được từ việc thực hiện liên tiếp phép đối xứng qua đường thẳng IJ và phép vị tự tâm B, tỉ số 2

Giải

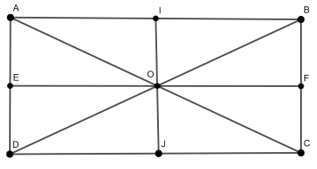
– Lấy đối xứng qua đường thẳng IJ

IJ là đường trung trực của AB và EF

Suy ra: D_IJ(A) = B; D_IJ(E) = F 

O ∈ IJ => D_IJ(O) = O => D_IJ(ΔAEE) = ΔBFO  

ΔBFO qua phép vị tự tâm B tỉ số 2

Ta có: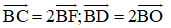   

Suy ra: C = V_(B;2) ; d = V_(B;2)(O) => ΔBCD = V_(B;2)(ΔBFO) 

Vậy ảnh của tam giác AEO qua phép đồng dạng theo đề bài là tam giác BCD

Ví dụ 4: Cho hai hình chữ nhật có tỉ số giữa chiều rộng và chiều dài bằng 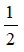. Chứng minh rằng luôn có một phép đồng dạng biến hình này thành hình kia

Giải

Giả sử ta có hai hình chữ nhật ABCD.A’B’C’D’ và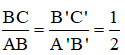 

Phép tịnh tiến 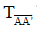 biến hình chữ nhật ABCD thành hình chữ nhật A^‘B₁C₁D₁ 

Phép quay Q_(A;α) với α = (A^‘B₁; A^‘B^‘) biến hình chữ nhật A^‘B₁C₁D₁ thành hình chữ nhật A’B₂C₂D₂ 

Vì 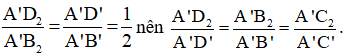 Từ đó suy ra phép vị tự V_(A’;k) với  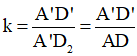sẽ biến hình chữ nhật thành A’B₂C₂D₂ thành hình chữ nhật A’B’C’D’

 Vậy phép đồng dạng có được bằng cách thực hiện liên tiếp các phép biến hình 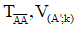 sẽ biến hình chữ nhật ABCD thành hình chữ nhật A’B’C’D’

Dạng 3: Dùng phép đồng dạng để giải toán

Phương pháp giải: Dùng các tính chất của phép đồng dạng

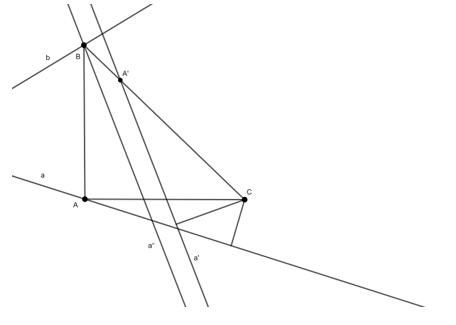
Ví dụ 5: Cho hai đường thẳng a và b cắt nhau và điểm C. Tìm trên a và b các điểm A và B tương ứng sao cho tam giác ABC vuông cân ở A.

Lời giải:

Ta thấy góc lượng giác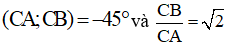 

Do đó có thể xem B là ảnh của A qua phép đồng dạng F có được bằng cách thực hiện liên tiếp phép quay tâm C, góc -45⁰ và phép vị tự tâm C, tỉ số √2 

Vì A ∈ a nên B ∈ a^” = F(a) , B lại thuộc a

Do đó B là giao của a” với b

Ví dụ 6: Cho tam giác ABC, dựng ra phía ngoài tam giác ABC các tam giác đều BCA’, CAB’, ABC’. Gọi  lần lượt là tâm của ba tam giác đều BCA’, CAB’, ABC’. Chứng minh tam giác O₁O₂O₃ là tam giác đều

Lời giải:

Để chứng minh tam giác O₁O₂O₃ là tam giác đều ta xét các phép đồng dạng sau:

Kí hiệu F(I,φ, k) = V_(I,k) Q_(I;φ)là phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay Q_(I;φ) và phép vị tự V_(I,k). Ta xét các phép đồng dạng:

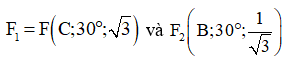
Gọi I, J, K, H là các điểm trên CA^‘,CA,BA^‘,BO₃,BO₁ sao cho CI = CO₁, CJ = CO₂, BK = BO₁, BH = AB, BE = BA^‘ khi đó

F₁(O₁) = V_(C,√3) Q_(C;30) (O₁) = V_(C,√3)(I) = A^‘ 

Tương tự:

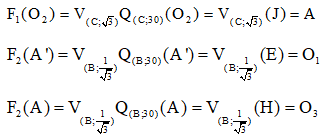
Vậy F₂F₁(O₂) = F₂(A) = O₃ và F₂F₁(O₁) = F₂(A^‘) = O₁ 

Mặt khác F = F₁F₂ là phép đồng dạng có tỉ số k = k₁k₂ = √3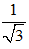 = 1 và φ₁ + φ₂ = 60⁰ nên F chính là phép quay tâm O₁ góc quay 60⁰ 

Do đó: Q_(O1,60⁰)(O₂) = O₃ nên tam giác O₁O₂O₃ là tam giác đều

III. Bài tập áp dụng

Bài 1: Chứng minh rằng hai đa giác đều có cùng số cạnh luôn đồng dạng với nhau

Bài 2: Cho hình thang ABCD có AB song song với CD, AD = a, DC = b còn hai đỉnh A, B cố định. Gọi I là giao điểm của hai đường chéo

a. Tìm tập hợp các điểm c khi D thay đổi

b. Tìm tập hợp các điểm I khi c và D thay đổi như trong câu a

Bài 3: Cho hình chữ nhật ABCD tâm I. Gọi E, F, G, H lần lượt là trung điểm của AB, CD, CI, FC. Phép đồng dạng hợp thành bởi phép vị tự tâm C tỉ số k = 2 và phép đối xứng tâm I biến tứ giác IGHF thành:

A. AIFD      

B. BCFI      

C. CIEB      

D. DIEA

Bài 4: Trong mặt phẳng tọa độ Oxy, phép đồng dạng F hợp thành bởi phép vị tự tâm O (0; 0) tỉ số k = 3 và phép đối xứng trục Ox, biến đường thẳng d: x – y – 1 = 0 thành đường thẳng d’ có phương trình:

A. x – y + 3 = 0

B. x + y – 3 = 0

C. x + y + 3 = 0

D. x – y + 2 = 0

Bài 5:  Cho điểm I (2; 1) điểm M (-1; 0) phép đồng dạng hợp thành bởi phép vị tự tâm I tỉ số k = -2 và phép đối xứng trục Ox biến M thành M’’ có tọa độ bao nhiêu ?

Bài 6: Trong mặt phẳng tọa độ Oxy cho hai điểm A (-2; -3) và B (4; 1). Phép đồng dạng tỉ số 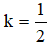 biến điểm A thành A’, biến điểm B thành B’. Tính độ dài A’B’

Bài 7: Trong các khẳng định sau, khẳng định nào sai?

A. Thực hiện liên tiếp hai phép đồng dạng thì được một phép đồng dạng

B. Phép dời hình là phép đồng dạng tỉ số k = 1

C. Phép vị tự có tính chất bảo toàn khoảng cách 

D. Phép vị tự không là phép dời hình

Bài 8: Cho hình vuông ABCD tâm O. M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. Phép dời hình nào sau đây biến tam giác AMO thành tam giác CPO?

A. Phép tịnh tiến vectơ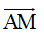  

B. Phép đối xứng trục MP

C. Phép quay tâm A góc quay 180 độ

D. Phép quay tâm O góc quay -180 độ

Bài 9: Phép biến hình có được bằng cách thực hiện liên tiếp hai phép biến hình sau đây là một phép đồng dạng tỉ số k = 3

A. Phép tịnh tiến và phép đồng nhất

B. Phép tịnh tiến và phép quay

C. Phép dời hình và phép vị tự tỉ số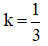  

D. Phép tịnh tiến và phép vị tự tỉ số k = -3

Bài 10: Phép đồng dạng F biến điểm M (x; y) thành M’ (x’; y’) thỏa mãn: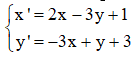   

Ảnh của điểm A (-2; 1) qua phép đồng dạng F là:

A. (6; 10)

B. (10; 6)

C. (6; -10)

D. (-6; 10)

Chương 1: Phép dời hình và phép đồng dạng

1.1 Phép tịnh tiến

1.1.1 Tóm tắt lí thuyết

Định nghĩa 1 .

Trong mặt phẳng cho vecto \(\overrightarrow v \). Phép biến hình biến mỗi điểm M thành điểm \({M^\prime }\) sao cho \(\overrightarrow {M{M^\prime }}  = \vec v\) được gọi là phép tịnh tiến theo véc-tơ \(\vec v\).

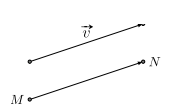
Phép tịnh tiến theo véc-tơ \(\vec v\) thường được lí hiệu là \({{\rm{T}}_{\vec v}},\vec v\) được gọi là véc-tơ tịnh tiến. Như vậy, \({{\rm{T}}_{\vec v}}(M) = {M^\prime } \Leftrightarrow \overrightarrow {M{M^\prime }}  = \vec v\).

Phép tịnh tiến theo véc-tơ – không chính là phép đồng nhất. (Biến mỗi điểm thành chính nó).

Tính chất 1 .

Biến 1 vecto thành vecto bằng nó. Nếu \[{{\rm{T}}_{\vec v}}(M) = M’\],\({{\rm{T}}_{\vec v}}(N) = {N^\prime }\) thì \(\overrightarrow {{M^\prime }{N^\prime }}  = \overrightarrow {MN} \). Biến đoạn thẳng thành đoạn thẳng bằng nó \({M^\prime }{N^\prime } = MN\).

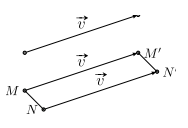
Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Dựng ảnh đường thẳng d qua \({{\rm{T}}_{\vec v}}\).

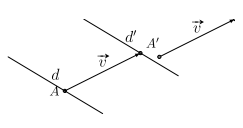
a) Lấy trên d một điểm A.

b) Dựng \({A^\prime }\) là ảnh của A.

c) Qua \({A^\prime }\) dựng đường thẳng cùng phương với d.

Đặc biệt: \({d^\prime } \equiv d\) khi và chỉ khi \(\vec v\) cùng phương với véc-tơ chỉ phương của d (hay \(\vec v\) có giá song song hoặc trùng với d).

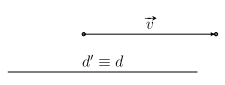
Tính chất 3 .

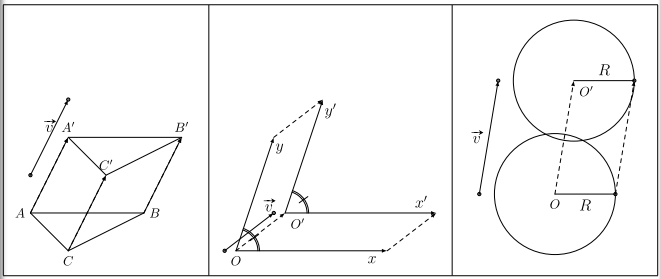
– Biến tam giác thành tam giác bằng nó.

– Biến một góc thành một góc có số đo bằng nó.

– Biến một đường tròn thành một đường tròn có bán kính bằng nó. Cách dựng ảnh của đường tròn

– Xác định tâm O và bán kính R của (C).

– Tìm ảnh \({O^\prime }\) của O.

– Dựng \(\left( {{C^\prime }} \right)\) có tâm \({O^\prime }\) và có bán kính \({R^\prime } = R\).

Tính chất 4. Nếu \({M^\prime }\) là ảnh của M qua \({T_{\vec v}}\) thì ngược lại M là ảnh của \({M^\prime }\) qua phép tịnh tiến theo \( – \vec v\).

Tính chất 5. Trong mặt phẳng tọa độ Oxy cho vecto \(\overrightarrow v  = \left( {a{\rm{ }};{\rm{ }}b} \right).\)Với mỗi điểm M(x;y) ta có \({M^\prime }\left( {{x^\prime };{y^\prime }} \right)\) là ảnh của M qua phép tịnh tiến theo \(\vec v\). Khi đó

\(\overrightarrow {M{M^\prime }}  = \vec v \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + a}\\{{y^\prime } = y + b.}\end{array}} \right.\)

(Tọa độ ảnh = tọa độ điểm + tọa độ véc-tơ tịnh tiến).

1.1.2 Các dạng toán và ví dụ mẫu

Dạng 1. Tìm ảnh, tạo ảnh của đường thẳng d qua một phép tịnh tiến theo véc-tơ \(\vec v\).

Phương pháp

– Lấy M trên d.

– Tìm ảnh \({M^\prime }\) của M.

– d’ là đường thẳng qua \({M^\prime }\) và song song hoặc trùng d.

Ví dụ 1. Trong mặt phẳng tọa độ Oxy cho véc-tơ \(\vec v = (1; – 5)\), đường thẳng \(d:3x + \) \(4y – 4 = 0\) Viết phương trình đường thẳng \({d^\prime }\) là ảnh của d qua phép tịnh tiến theo véc-tơ \(\vec v\).

Dạng 2. Tìm tạo ảnh của đường thẳng d qua một phép tịnh tiến theo véc-tơ \(\vec v\)

– Lấy \({M^\prime }\) trên \({d^\prime }\).

– Tìm M sao cho \({M^\prime }\) là ảnh của M.

– Vậy \({d^\prime }\) là đường thẳng qua M và song song hoặc trùng d.

Ví dụ 2. Trên mặt phẳng tọa độ Oxy phép tịnh tiến theo vecto \[\overrightarrow v  = \left( {3{\rm{ }};{\rm{ }}1} \right)\]biến đường thẳng d thành đường thẳng \({d^\prime }\), biết \({d^\prime }\) phương trình \(x – 2y = 0\). Viết phương trình d.

Dạng 3. Tìm cảnh của đường tròn (C ) qua 1 phép tịnh tiến theo vecto \(\overrightarrow v \)

Phương pháp

– Tìm tâm I và bán kính \({R^\prime }\) của đường tròn (C).

– Tìm ảnh \({I^\prime }\) của I qua phép tịnh tiến này.

– Đường tròn \(\left( {{C^\prime }} \right)\) là ảnh của (C) là đường tròn có tâm \({I^\prime }\) và bán kính \({R^\prime } = R\).

Ví dụ 3. Cho đường tròn \((C):{x^2} + {y^2} + 4x – 6y – 12 = 0\). Viết phương trình đường tròn \(\left( {{C^\prime }} \right)\) là ảnh của (C) qua phép tịnh tiến theo véc-tơ \(\vec u = (2; – 3)\).

Dạng 4. Tìm tạo ảnh của đường tròn \((C’)\) qua 1 phép tịnh tiến theo vecto \(\overrightarrow v \)

Phương pháp

– Tìm tâm \({I^\prime }\) và bán kính \({R^\prime }\) của đường tròn \(\left( {{C^\prime }} \right)\).

– Tìm I sao cho \({I^\prime }\) là ảnh của I qua phép tịnh tiến này.

– Đường tròn (C) là đường tròn có tâm I và bán kính \(R = {R^\prime }\).

Ví dụ 4. Cho đường tròn \((C):{(x – 1)^2} + {(y + 2)^2} = 4\). Viết phương trình đường tròn \(\left( {{C^\prime }} \right)\) sao cho (C) là ảnh của \(\left( {{C^\prime }} \right)\) qua phép tịnh tiến theo véc-tơ \(\vec u = (2;3)\).

Dạng 5. Tìm ảnh của một đường cong (P) qua một phép tịnh tiến theo \(\vec u = (a;b)\)

Phương pháp

– Xét \(A(x;y) \in (P)\), ảnh của A là \({A^\prime }\left( {{x^\prime };{y^\prime }} \right)\), ta có \(\left\{ {\begin{array}{*{20}{l}}{{x^\prime } = x + a}\\{{y^\prime } = y + b}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = {x^\prime } – a}\\{y = {y^\prime } – b{\rm{. }}}\end{array}} \right.} \right.\)

– Do \(A(x;y) \in (P)\) nên x, y thỏa mãn phương trình (P).

– Thay x, y bởi \({x^\prime };{y^\prime }\) ở hệ thức trên ta được một đẳng thức theo \({x^\prime };{y^\prime }\).

– \({A^\prime }\left( {{x^\prime };{y^\prime }} \right)\) thỏa mãn phương trình này nên \({A^\prime }\left( {{x^\prime };{y^\prime }} \right)\) thuộc đường cong \(\left( {{P^\prime }} \right)\).

Ví dụ 5. Trong mặt phẳng tọa độ (Oxy), cho parabol \((P):y =  – {x^2} + 2x + 1\). Viết phương trình ảnh của (P) qua phép tịnh tiến theo \(\vec v = (0;1)\).

Dạng 6. Tìm tạo ảnh của một đường cong (P) qua một phép tịnh tiến theo \(\vec u = (a;b)\)

Phương pháp

– Xét \(A(x;y) \in (P)\), điểm \({A^\prime }\left( {{x^\prime };{y^\prime }} \right)\) là tạo ảnh của A. Khi đó ta có \(\left\{ {\begin{array}{*{20}{l}}{x = {x^\prime } + a}\\{y = {y^\prime } + b}\end{array}} \right.\)

– Do \(A(x;y) \in (P)\) nên x, y thỏa mãn phương trình (P).

– Thay x, y bởi \({x^\prime },{y^\prime }\) ở hệ thức trên ta được một đẳng thức theo \({x^\prime },{y^\prime }\).

– \({A^\prime }\left( {{x^\prime };{y^\prime }} \right)\) thỏa mãn phương trình này nên \({A^\prime }\left( {{x^\prime };{y^\prime }} \right)\) thuộc đường cong \(\left( {{P^\prime }} \right)\).

Ví dụ 6. Trong mặt phẳng tọa độ (Oxy), cho parabol \((P):y =  – {x^2} + 2x + 1\). Viết phương trình \(\left( {{P^\prime }} \right)\) sao cho qua phép tịnh tiến theo \(\vec v = (1;1)\) thì (P) là ảnh của \(\left( {{P^\prime }} \right)\).

Dạng 7. Xác định vecto tịnh tiến

Ví dụ 7. Trong mặt phẳng với hệ tọa độ O x y, cho hai parabol \((P):y = {x^2}\) và \((Q):y = \) \({x^2} + 2x + 2\). Tìm phép tịnh tiến \({{\rm{T}}_{\vec v}}\) biến (Q) thành (P).

Dạng 8. Ứng dụng phép tịnh tiến vào các bài toán hình học sơ cấp

Ví dụ 8. Cho tam giác ABC có diện tích bằng 72 . Gọi \({A_1},{B_1},{C_1}\) là các trung điểm của ba cạnh BC, CA, AB. Gọi \({I_1},{I_2},{I_3}\) tương ứng là các tâm đường tròn nội tiếp của ba tam giác \(A{B_1}{C_1},B{C_1}{A_1},C{A_1}{B_1}\). Tính diện tích tam giác \(\Delta {I_1}{I_2}{I_3}\).

Ví dụ 9. Cho tam giác ABC. Cho hai điểm D, E lần lượt di động trên tia đối của các tia BA, CA sao cho BD=EC. Tìm tập hợp trung điểm của DE.

Dạng 9. Các bài toán thực tế

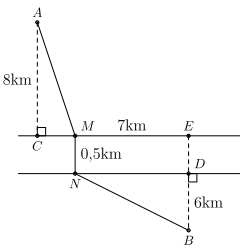
Ví dụ 10 .

Hai thị trấn A, B nằm ở hai phía một con sông như hình bên. Người ta muốn dựng một cầu, M N vuông góc với hai bờ sông và 2 đường cao tốc AM, BN. Vị trí M trên bờ sông để tổng độ dài hai đoạn cao tốc AM, BN nhỏ nhất. Biết \(CE = 7\;{\rm{km}},MN = 0,5\;{\rm{km}},DB = 6\) \({\rm{km}}\). Tính CM.

1.1.3 Bài tập trắc nghiệm

Câu 1. Trong mặt phẳng tọa độ Oxy, cho tam giác A B C. Gọi M, N, P lần lượt là trung điểm các cạnh BC, CA, AB. Phép tịnh tiến vecto \(\overrightarrow v  = \frac{1}{2}\overrightarrow {BC} \)  biến

A. điểm P thành điểm N.

B. điểm N thành điểm P.

C. điểm M thành điểm B.

D. điểm M thành điểm N.

Câu 2. Cho tam giác có trọng tâm G. Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai?

A. \({T_{\frac{3}{2}}}\overrightarrow {DG} (FE) = BC\).

B. \({T_{\frac{1}{2}}}\overrightarrow {BC} (EF) = EF\).

C. \({T_{\frac{1}{2}}}\overrightarrow {BC} (FD) = AC\).

D. \({T_{2\overrightarrow {DG} }}(AG) = GD\).

Câu 3. Ảnh của điểm M(0;1) qua phép tịnh tiến theo véc-tơ \(\vec u = (1;2)\) là điểm nào?

A. \({M^\prime }(2;3)\).

B. \({M^\prime }(1;3)\).

C. \({M^\prime }(1;1)\).

D. \({M^\prime }( – 1; – 1)\).

Câu 4. Phép tịnh tiến theo \(\vec v\) biến điểm A(1;3) thành điểm \({A^\prime }(1;7)\). Tìm tọa độ của véc-tơ tịnh tiến \(\vec v\) ?

A. \(\vec v = (0; – 4)\).

B. \(\vec v = (4;0)\).

C. \(\vec v = (0;4)\).

D. \(\vec v = (0;5)\).

Câu 5. Trong mặt phẳng Oxy, cho đường thẳng \(\Delta 😡 – 2y + 2 = 0\). Ảnh của đường thẳng \(\Delta \) qua phép tịnh tiến theo \(\vec u = (2;3)\) có phương trình là

A. \(x – 2y + 6 = 0\).

B. \(x + 2y + 2 = 0\).

C. \(2x – y + 2 = 0\).

D. \(2x + y + 2 = 0\).

Câu 6. Trong mặt phẳng tọa độ O x y, phép tịnh tiến biến đường thẳng \(d:x + y + 1 = 0\) thành đường thẳng \({d^\prime }:x + y – 1 = 0\) theo véc-tơ cùng phương với véc-tơ \(\vec i\). Hãy tìm vec-tơ tịnh tiến

A. \(\vec v = (2;0)\).

B. \(\vec v = (0;2)\).

C. \(\vec v = (0; – 2)\).

D. \(\vec v = ( – 2;0)\).

Câu 7. Trong mặt phẳng Oxy, phép tịnh tiến theo vecto \(\overrightarrow v (2{\rm{ }}; – 3)\) biến đường thẳng \(d:2x + \) \(3y – 1 = 0\) thành đường thẳng \({d^\prime }\) có phương trình:

A. \({d^\prime }:3x + 2y – 1 = 0\).

B. \({d^\prime }:2x + 3y + 4 = 0\).

C. \({d^\prime }:3x + 2y + 1 = 0\).

D. \({d^\prime }:2x + 3y + 1 = 0\).

Câu 8. Trên mặt phẳng tọa độ, phép tịnh tiến theo véc-tơ \(\vec v(3;1)\) biến đường thẳng d thành đường thẳng \({d^\prime }\), biết \({d^\prime }:x – 2y = 0\). Khi đó d có phương trình là

A. \(x – 2y – 1 = 0\).

B. \(x – 2y + 1 = 0\).

C. \(x + 2y – 1 = 0\).

D. \(x + 2y – 1 = 0\).

Câu 9. Phép tịnh tiến theo \(\vec v\) biến điểm A(1;3) thành điểm \({A^\prime }(1;7)\). Tìm tọa độ của véc-tơ tịnh tiến \(\vec v\) ?

A. \(\vec v = (0; – 4)\).

B. \(\vec v = (4;0)\).

C. \(\vec v = (0;4)\).

D. \(\vec v = (0;5)\).

Xem thêm