50 Bài tập Vi phân (có đáp án)- Toán 11

Bài tập Toán 11 Chương 5 Bài 4: Vi phân

A. Bài tập Vi phân

I. Bài tập trắc nghiệm

Bài 1: Tìm vi phân của các hàm số y = x³ + 2x²

A. dy = (3x² – 4x)dx

B. dy = (3x² + x)dx

C. dy = (3x² + 2x)dx

D. dy = (3x² + 4x)dx

Lời giải:

Chọn đáp án D

Bài 2: Tìm vi phân của các hàm số 

Lời giải:

Chọn đáp án A

Bài 3: Tìm vi phân của các hàm số y = sin2x + sin3x

A. dy = (cos²x + 3sin²xcosx)dx

B. dy = (2cos²x + 3sin²xcosx)dx

C. dy = (2cos²x + sin²xcosx)dx

D. dy = (cos²x + sin²xcosx)dx

Lời giải:

Chọn đáp án A

Bài 4: Cho hàm số . Vi phân của hàm số là:

 

Lời giải:

Chọn đáp án D

Bài 5: Vi phân của hàm số  là:

Lời giải:

Chọn đáp án C

Bài 6: Cho hàm số . Vi phân của hàm số tại x = -3 là:

Lời giải:

Chọn đáp án A

Bài 7: Hàm số . Tính vi phân của hàm số tại x = 0,01 và ∆x = 0,01?

A. 9.

B. -9.

C. 90.

D. -90.

Lời giải:

Chọn đáp án D

Bài 8: Cho hàm số y = x³ – 2x² + 2 . Tính vi phân của hàm số tại điểm x₀ = 1, ứng với số gia ∆x = 0,02.

A. -0,02

B. 0,01

C. 0,4

D. -0,06

Lời giải:

Chọn đáp án A

Bài 9: Tính gần đúng giá trị sin46°

Lời giải:

Chọn đáp án C

Bài 10: Tính gần đúng giá trị 

A. 1,0004

B. 1,0035

C. 1,00037

D.1,0005

Lời giải:

Chọn đáp án D

II. Bài tập tự luận có lời giải

Bài 1: Cho hàm số y = f(x) = (x – 1)². Biểu thức nào sau đây chỉ vi phân của hàm số f(x) ?

Lời giải:

Bài 2: Tìm vi phân của các hàm số y = tan2x

Lời giải:

Bài 3: Xét hàm số . Chọn câu đúng:

Lời giải:

Bài 4: Cho hàm số . Vi phân của hàm số là:

Bài 5: Hàm số y = xsinx + cosx có vi phân là:

Bài 6: Vi phân của hàm số f(x) = 3x² – x tại điểm x = 2, ứng với ∆x = 0,1 là:

Bài 7: Tính gần đúng giá trị  (lấy 4 chữ số thập phân trong kết quả).

Lời giải:

Bài 8: Tính gần đúng giá trị cos30°15’

Lời giải:

Bài 9: Tìm vi phân của các hàm số sau:

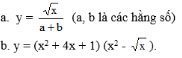
Lời giải:

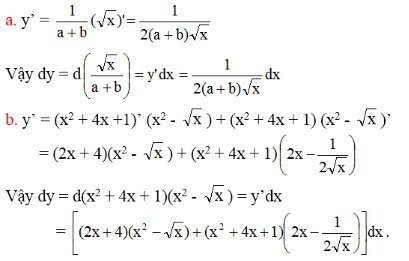
Bài 10 Tìm dy, biết:

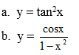
Lời giải:

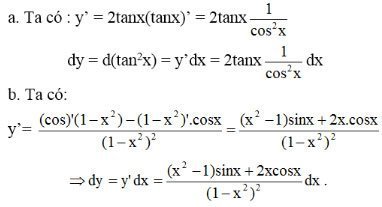
III. Bài tập vận dụng

Bài 1 Tìm vi phân của các hàm số sau:

a) $y=\frac{\sqrt{x}}{a+b}$ ($a,b$ là hằng số)

b) $y=(x^2+4x+1)(x^2-\sqrt{x})$

Bài 2 Tìm $dy$, biết:

a) $y={\tan }^{2}x$

b) $y=\frac{\cos x}{1-x^2}$.

Bài 3 Tìm vi phân của các hàm số y = x³ + 2x²

Bài 4 Tìm vi phân của các hàm số 

Bài 5 Tìm vi phân của các hàm số y = sin2x + sin³x

Bài 6 Cho hàm số . Vi phân của hàm số là?

Bài 7 Vi phân của hàm số  là?

Bài 8 Cho hàm số . Vi phân của hàm số tại x = -3 là?

Bài 9 Hàm số . Tính vi phân của hàm số tại x = 0,01 và ∆x = 0,01?

Bài 10 Cho hàm số y = x³ – 2x² + 2 . Tính vi phân của hàm số tại điểm x₀ = 1, ứng với số gia ∆x = 0,02.

B. Lý thuyết Vi phân

Cho hàm số f^(n–1)(x) xác định trên khoảng (a; b) và có đạo hàm tại x ∈ (a; b). Giả sử f^(n–1)(x) (n ∈ N, n ≥ 4) là số gia của x.

Ta gọi tích f’(x₀)Δx là vi phân của hàm số n – 1 tại x ứng với số gia Δx, kí hiệu là y = f(x) hoặc dy, tức là

        dy = df(x) = f’(x)Δx

Chú ý:

    + Áp dụng định nghĩa trên vào hàm số y = x, ta có dx = d(x) = (x)’Δx = 1.Δx = Δx.

    + Do đó, với hàm số y = f(x) ta có dy = df(x) = f’(x)Δx.